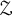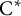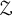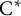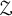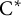1 Introduction
The Jiang–Su algebra
![]() ${\mathcal {Z}}$
has become a cornerstone in the classification program of simple nuclear
${\mathcal {Z}}$
has become a cornerstone in the classification program of simple nuclear
![]() $\mathrm {C}^*$
-algebras [Reference Jiang and Su28]. Tensorial absorption of this algebra, reminiscent of the McDuff property for
$\mathrm {C}^*$
-algebras [Reference Jiang and Su28]. Tensorial absorption of this algebra, reminiscent of the McDuff property for
![]() $\mathrm {II}_1$
factors, is a regularity condition which forms part of the Toms–Winter regularity conjecture [Reference Toms and Winter57], and it allows separable, simple, unital, and nuclear
$\mathrm {II}_1$
factors, is a regularity condition which forms part of the Toms–Winter regularity conjecture [Reference Toms and Winter57], and it allows separable, simple, unital, and nuclear
![]() $\mathrm {C}^*$
-algebras in the UCT class to be classified by their K-theoretical and tracial data [Reference Castillejos, Evington, Tikuisis, White and Winter14, Reference Elliott, Gong, Lin and Niu18, Reference Gong, Lin and Niu25, Reference Gong, Lin and Niu26, Reference Tikuisis, White and Winter56, Reference Winter60, Reference Winter61]. Even outside the nuclear setting, tensorial absorption of
$\mathrm {C}^*$
-algebras in the UCT class to be classified by their K-theoretical and tracial data [Reference Castillejos, Evington, Tikuisis, White and Winter14, Reference Elliott, Gong, Lin and Niu18, Reference Gong, Lin and Niu25, Reference Gong, Lin and Niu26, Reference Tikuisis, White and Winter56, Reference Winter60, Reference Winter61]. Even outside the nuclear setting, tensorial absorption of
![]() ${\mathcal {Z}}$
is a useful condition. For instance, Rørdam showed that this condition implies almost unperforation of the Cuntz semigroup [Reference Rørdam48].
${\mathcal {Z}}$
is a useful condition. For instance, Rørdam showed that this condition implies almost unperforation of the Cuntz semigroup [Reference Rørdam48].
For the class of simple and unital
![]() $\mathrm {C}^*$
-algebras, Hirshberg and Orovitz [Reference Hirshberg and Orovitz27] introduced the notion of tracial
$\mathrm {C}^*$
-algebras, Hirshberg and Orovitz [Reference Hirshberg and Orovitz27] introduced the notion of tracial
![]() ${\mathcal {Z}}$
-stability, which corresponds to a weakened form of tensorial absorption of the Jiang–Su algebra
${\mathcal {Z}}$
-stability, which corresponds to a weakened form of tensorial absorption of the Jiang–Su algebra
![]() ${\mathcal {Z}}$
. The weaker nature of this notion makes it easier to verify than tensorial absorption of
${\mathcal {Z}}$
. The weaker nature of this notion makes it easier to verify than tensorial absorption of
![]() ${\mathcal {Z}}$
in many examples from dynamical systems (see, for instance, [Reference Kerr29–Reference Kerr and Szabó31, Reference Ma and Wu38, Reference Naryshkin41, Reference Niu44]). Despite its apparent weaker form, it turns out to be equivalent to tensorial absorption of
${\mathcal {Z}}$
in many examples from dynamical systems (see, for instance, [Reference Kerr29–Reference Kerr and Szabó31, Reference Ma and Wu38, Reference Naryshkin41, Reference Niu44]). Despite its apparent weaker form, it turns out to be equivalent to tensorial absorption of
![]() ${\mathcal {Z}}$
in the presence of nuclearity. Therefore, all such examples where one can directly verify tracial
${\mathcal {Z}}$
in the presence of nuclearity. Therefore, all such examples where one can directly verify tracial
![]() ${\mathcal {Z}}$
-stability are within the scope of the classification program.
${\mathcal {Z}}$
-stability are within the scope of the classification program.
In recent years, there has been an uptick in interest concerning the classification program beyond unital
![]() $\mathrm {C}^*$
-algebras [Reference Elliott, Gong, Lin and Niu16, Reference Elliott, Gong, Lin and Niu17, Reference Gong and Lin22–Reference Gong and Lin24, Reference Lin37, Reference Nawata43]. So it is natural to consider and study tracial
$\mathrm {C}^*$
-algebras [Reference Elliott, Gong, Lin and Niu16, Reference Elliott, Gong, Lin and Niu17, Reference Gong and Lin22–Reference Gong and Lin24, Reference Lin37, Reference Nawata43]. So it is natural to consider and study tracial
![]() ${\mathcal {Z}}$
-stability for general simple
${\mathcal {Z}}$
-stability for general simple
![]() $C^*$
-algebras, which may not be unital. This notion was announced by Amini, Golestani, Jamali, and Phillips and very recently appeared in [Reference Amini, Golestani, Jamali and Phillips1]. This paper aims to study the relation between tracial
$C^*$
-algebras, which may not be unital. This notion was announced by Amini, Golestani, Jamali, and Phillips and very recently appeared in [Reference Amini, Golestani, Jamali and Phillips1]. This paper aims to study the relation between tracial
![]() ${\mathcal {Z}}$
-stability and tensorial absorption of
${\mathcal {Z}}$
-stability and tensorial absorption of
![]() ${\mathcal {Z}}$
in this setting.
${\mathcal {Z}}$
in this setting.
In particular, we show that it is preserved under stable isomorphisms and that it implies almost unperforation of the Cuntz semigroup. Our main theorem is the following.
Theorem A Let A be a separable simple nuclear
![]() $\mathrm {C}^*$
-algebra. Then A is tracially
$\mathrm {C}^*$
-algebra. Then A is tracially
![]() ${\mathcal {Z}}$
-stable if and only if A is
${\mathcal {Z}}$
-stable if and only if A is
![]() ${\mathcal {Z}}$
-stable.
${\mathcal {Z}}$
-stable.
It is a rather straightforward consequence of the definition that tracial
![]() ${\mathcal {Z}}$
-stability yields the existence of tracially large order zero maps from matrix algebras into the central sequence algebra of A; a condition that we will refer to as the uniform McDuff property. Not unlike in Hirshberg–Orovitz’s original approach, the most significant step toward the main theorem is to show that the Cuntz semigroup of any tracially
${\mathcal {Z}}$
-stability yields the existence of tracially large order zero maps from matrix algebras into the central sequence algebra of A; a condition that we will refer to as the uniform McDuff property. Not unlike in Hirshberg–Orovitz’s original approach, the most significant step toward the main theorem is to show that the Cuntz semigroup of any tracially
![]() ${\mathcal {Z}}$
-stable
${\mathcal {Z}}$
-stable
![]() $\mathrm {C}^*$
-algebra is almost unperforated. In the presence of nuclearity, this grants us access to property (SI), which allows us to make the jump to genuine
$\mathrm {C}^*$
-algebra is almost unperforated. In the presence of nuclearity, this grants us access to property (SI), which allows us to make the jump to genuine
![]() ${\mathcal {Z}}$
-stability with Matui–Sato’s [Reference Matui and Sato40] famous technique (see Section 5).
${\mathcal {Z}}$
-stability with Matui–Sato’s [Reference Matui and Sato40] famous technique (see Section 5).
We hope that this version of tracial
![]() ${\mathcal {Z}}$
-stability will have potential applications in the study of
${\mathcal {Z}}$
-stability will have potential applications in the study of
![]() ${\mathcal {Z}}$
-stability for algebras arising from group actions on general
${\mathcal {Z}}$
-stability for algebras arising from group actions on general
![]() $\mathrm {C}^*$
-algebras (see, for instance, [Reference Amini, Golestani, Jamali and Phillips2]).
$\mathrm {C}^*$
-algebras (see, for instance, [Reference Amini, Golestani, Jamali and Phillips2]).
Structure of the paper
In Section 2, we gather some preliminaries needed for this note. In particular, we introduce a non-unital version of the uniform McDuff property and state its relation with uniform property
![]() $\Gamma $
. Our version of tracial
$\Gamma $
. Our version of tracial
![]() ${\mathcal {Z}}$
-stability is introduced in Section 3, where we also show that it is preserved under stable isomorphisms. In Section 4, we prove that tracial
${\mathcal {Z}}$
-stability is introduced in Section 3, where we also show that it is preserved under stable isomorphisms. In Section 4, we prove that tracial
![]() ${\mathcal {Z}}$
-stability yields almost unperforation of the Cuntz semigroup. Finally, the equivalence between
${\mathcal {Z}}$
-stability yields almost unperforation of the Cuntz semigroup. Finally, the equivalence between
![]() ${\mathcal {Z}}$
-stability and tracial
${\mathcal {Z}}$
-stability and tracial
![]() ${\mathcal {Z}}$
-stability for nuclear algebras is established in Section 5.
${\mathcal {Z}}$
-stability for nuclear algebras is established in Section 5.
Remark The notion of tracial
![]() ${\mathcal {Z}}$
-stability for non-unital
${\mathcal {Z}}$
-stability for non-unital
![]() $\mathrm {C}^*$
-algebras is also introduced and discussed in [Reference Amini, Golestani, Jamali and Phillips1], which was posted online sometime after this note was uploaded to the arXiv in 2021. Some of the related results (overlapping with Sections 3 and 4) were announced by some of the authors of [Reference Amini, Golestani, Jamali and Phillips1] at a preliminary stage at the 2018 ICM satellite conference in Rio de Janeiro (attended by the second author of this note) and COSy 2021 (attended by the first and second authors of this note). Although we claim no originality for some of the results in Sections 3 and 4, we had to ensure a self-contained treatment of our findings at the time of posting this note by supplying our own proofs (which are not necessarily identical to the ones in [Reference Amini, Golestani, Jamali and Phillips1]) to all claims made there. Shortly after this note was posted, the preprint [Reference Fu, Li and Lin21] appeared on arXiv where the authors developed similar ideas with the goal of finding conditions that yield stable rank one.
$\mathrm {C}^*$
-algebras is also introduced and discussed in [Reference Amini, Golestani, Jamali and Phillips1], which was posted online sometime after this note was uploaded to the arXiv in 2021. Some of the related results (overlapping with Sections 3 and 4) were announced by some of the authors of [Reference Amini, Golestani, Jamali and Phillips1] at a preliminary stage at the 2018 ICM satellite conference in Rio de Janeiro (attended by the second author of this note) and COSy 2021 (attended by the first and second authors of this note). Although we claim no originality for some of the results in Sections 3 and 4, we had to ensure a self-contained treatment of our findings at the time of posting this note by supplying our own proofs (which are not necessarily identical to the ones in [Reference Amini, Golestani, Jamali and Phillips1]) to all claims made there. Shortly after this note was posted, the preprint [Reference Fu, Li and Lin21] appeared on arXiv where the authors developed similar ideas with the goal of finding conditions that yield stable rank one.
2 Preliminaries
2.1 Notation
Let A be a
![]() $\mathrm {C}^*$
-algebra. We will denote the unitization of A by
$\mathrm {C}^*$
-algebra. We will denote the unitization of A by
![]() $\tilde {A}$
, and the set of positive elements in A by
$\tilde {A}$
, and the set of positive elements in A by
![]() $A_+$
. The Pedersen ideal of A will be denoted by
$A_+$
. The Pedersen ideal of A will be denoted by
![]() $\mathrm {Ped}(A)$
. We will write
$\mathrm {Ped}(A)$
. We will write
![]() $\mathbb {K}$
for the algebra of compact operators on a separable infinite-dimensional Hilbert space, and we will denote its standard matrix units by
$\mathbb {K}$
for the algebra of compact operators on a separable infinite-dimensional Hilbert space, and we will denote its standard matrix units by
![]() $(e_{ij})$
. We will frequently identify
$(e_{ij})$
. We will frequently identify
![]() $M_n(\mathbb {C})$
with the subalgebra generated by
$M_n(\mathbb {C})$
with the subalgebra generated by
![]() $e_{ij}$
with
$e_{ij}$
with
![]() $1\leq i,j \leq n$
.
$1\leq i,j \leq n$
.
The cone of lower semicontinuous (extended) traces on A (see [Reference Elliott, Robert and Santiago19, Section 3]) will be denoted by
![]() $T^+(A)$
, and the set of tracial states on A will be denoted by
$T^+(A)$
, and the set of tracial states on A will be denoted by
![]() $T(A)$
. We say that A is traceless when
$T(A)$
. We say that A is traceless when
![]() $T^+(A)$
only consists of traces with values in
$T^+(A)$
only consists of traces with values in
![]() $\{0,\infty \}$
. If A is in addition simple, then there are precisely two (trivial) such traces denoted by the symbols
$\{0,\infty \}$
. If A is in addition simple, then there are precisely two (trivial) such traces denoted by the symbols
![]() $0$
and
$0$
and
![]() $\infty $
, and the negation of A being traceless is symbolically denoted by
$\infty $
, and the negation of A being traceless is symbolically denoted by
![]() $T^+(A)\neq \{0,\infty \}$
. Every lower semicontinuous trace on
$T^+(A)\neq \{0,\infty \}$
. Every lower semicontinuous trace on
![]() $\tau $
on A extends uniquely to the lower semicontinuous trace
$\tau $
on A extends uniquely to the lower semicontinuous trace
![]() $\tau \otimes \mathrm {Tr}$
on
$\tau \otimes \mathrm {Tr}$
on
![]() $A \otimes \mathbb {K}$
, where
$A \otimes \mathbb {K}$
, where
![]() $\mathrm {Tr}$
is the canonical unnormalized trace on
$\mathrm {Tr}$
is the canonical unnormalized trace on
![]() $\mathbb {K}$
[Reference Blanchard and Kirchberg8, Remark 2.27(viii)]. In fact, by uniqueness of
$\mathbb {K}$
[Reference Blanchard and Kirchberg8, Remark 2.27(viii)]. In fact, by uniqueness of
![]() $\mathrm {Tr}$
(see, for instance, [Reference Rørdam49, p. 8885]), every lower semicontinuous trace on
$\mathrm {Tr}$
(see, for instance, [Reference Rørdam49, p. 8885]), every lower semicontinuous trace on
![]() $A \otimes \mathbb {K}$
is of this form.Footnote
1
We will use this fact freely. We will also simply say trace instead of lower semicontinuous trace.
$A \otimes \mathbb {K}$
is of this form.Footnote
1
We will use this fact freely. We will also simply say trace instead of lower semicontinuous trace.
Given a
![]() $\mathrm {C}^*$
-algebra B and a map
$\mathrm {C}^*$
-algebra B and a map
![]() $\varphi : A \to B$
, if
$\varphi : A \to B$
, if
![]() $\mathfrak F \subseteq B$
is a subset, we write
$\mathfrak F \subseteq B$
is a subset, we write
![]() $\|[\varphi , \mathfrak {F}]\|< \epsilon $
to mean that
$\|[\varphi , \mathfrak {F}]\|< \epsilon $
to mean that
![]() $\|[\varphi (a),b]\|< \epsilon $
for any contractions
$\|[\varphi (a),b]\|< \epsilon $
for any contractions
![]() $a \in A$
and
$a \in A$
and
![]() $b \in \mathfrak {F}$
. We will use
$b \in \mathfrak {F}$
. We will use
![]() $a \approx _{\epsilon } b$
to denote
$a \approx _{\epsilon } b$
to denote
![]() $\|a-b\|<\epsilon $
. If
$\|a-b\|<\epsilon $
. If
![]() $a\in A_+$
and
$a\in A_+$
and
![]() $\epsilon>0$
, then
$\epsilon>0$
, then
![]() $(a-\epsilon )_+$
denotes the positive part of the self-adjoint element
$(a-\epsilon )_+$
denotes the positive part of the self-adjoint element
![]() $a-\epsilon 1_{\tilde {A}}$
.
$a-\epsilon 1_{\tilde {A}}$
.
As usual, given a free ultrafilter
![]() $\omega $
on
$\omega $
on
![]() $\mathbb {N}$
, we denote the
$\mathbb {N}$
, we denote the
![]() $\mathrm {C}^*$
-ultrapower of A by
$\mathrm {C}^*$
-ultrapower of A by
![]() $A_{\omega }:=\ell ^{\infty }(A)/\{(a_n)_{n \in \mathbb {N} }|\lim _{n\to \omega }\|a_n\|=0\}$
. For any subalgebra
$A_{\omega }:=\ell ^{\infty }(A)/\{(a_n)_{n \in \mathbb {N} }|\lim _{n\to \omega }\|a_n\|=0\}$
. For any subalgebra
![]() $D\subset A_{\omega }$
, we denote
$D\subset A_{\omega }$
, we denote
![]() $A_{\omega } \cap D'=\{x\in A_{\omega } \mid [x,D]=\{0\} \}$
and
$A_{\omega } \cap D'=\{x\in A_{\omega } \mid [x,D]=\{0\} \}$
and
![]() $A_{\omega } \cap D^{\perp } = \{x \in A_{\omega } \mid xD = Dx = \{0\}\}$
. The (corrected) central sequence algebra (see [Reference Kirchberg32, Definition 1.1])
$A_{\omega } \cap D^{\perp } = \{x \in A_{\omega } \mid xD = Dx = \{0\}\}$
. The (corrected) central sequence algebra (see [Reference Kirchberg32, Definition 1.1])
![]() $F_{\omega }(A)$
of a
$F_{\omega }(A)$
of a
![]() $\sigma $
-unital
$\sigma $
-unital
![]() $\mathrm {C}^*$
-algebra A is given by the quotient
$\mathrm {C}^*$
-algebra A is given by the quotient
2.2 Functional calculus of order zero maps
A c.p. map
![]() $\varphi : A \to B$
between
$\varphi : A \to B$
between
![]() $\mathrm {C}^*$
-algebras has order zero if it preserves orthogonality, i.e.,
$\mathrm {C}^*$
-algebras has order zero if it preserves orthogonality, i.e.,
![]() $\varphi (a)\varphi (b)=0$
if
$\varphi (a)\varphi (b)=0$
if
![]() $a,b\in A_+$
satisfy
$a,b\in A_+$
satisfy
![]() $ab=0$
. By the structure theorem proved by Winter and Zacharias [Reference Winter and Zacharias62, Theorem 3.3],
$ab=0$
. By the structure theorem proved by Winter and Zacharias [Reference Winter and Zacharias62, Theorem 3.3],
![]() $\varphi : A \to B$
has order zero if and only if there are
$\varphi : A \to B$
has order zero if and only if there are
![]() $h\in \mathcal M(\mathrm {C}^*(\varphi (A)))_+$
and a
$h\in \mathcal M(\mathrm {C}^*(\varphi (A)))_+$
and a
![]() $^*$
-homomorphism
$^*$
-homomorphism
![]() $\pi : A \to \mathcal M(\mathrm {C}^*(\varphi (A)))\cap \{h\}'$
such that
$\pi : A \to \mathcal M(\mathrm {C}^*(\varphi (A)))\cap \{h\}'$
such that
![]() $\varphi (a) = h \pi (a)$
for
$\varphi (a) = h \pi (a)$
for
![]() $a\in A$
. If A is unital, h is equal to
$a\in A$
. If A is unital, h is equal to
![]() $\varphi (1)$
. Using this decomposition, for any positive function
$\varphi (1)$
. Using this decomposition, for any positive function
![]() $f \in C_0(0,1]$
, one can define a new c.p. order zero map
$f \in C_0(0,1]$
, one can define a new c.p. order zero map
![]() $f(\varphi ): A \to B$
by
$f(\varphi ): A \to B$
by
![]() $f(\varphi )(a)=f(h)\pi (a)$
for
$f(\varphi )(a)=f(h)\pi (a)$
for
![]() $a\in A$
(see [Reference Winter and Zacharias62, Corollary 4.2]).
$a\in A$
(see [Reference Winter and Zacharias62, Corollary 4.2]).
2.3 Cuntz equivalence and strict comparison
Given
![]() $a,b \in A_+$
, it is said that a is Cuntz-below b, denoted
$a,b \in A_+$
, it is said that a is Cuntz-below b, denoted
![]() $a \precsim _A b$
, if for any
$a \precsim _A b$
, if for any
![]() $\epsilon>0$
there is
$\epsilon>0$
there is
![]() $x\in A$
such that
$x\in A$
such that
![]() $x^*bx \approx _{\epsilon } a$
. We will often simply write
$x^*bx \approx _{\epsilon } a$
. We will often simply write
![]() $\precsim $
if the relevant
$\precsim $
if the relevant
![]() $\mathrm {C}^*$
-algebra is understood from the context. It is said that a is Cuntz-equivalent to b, denoted by
$\mathrm {C}^*$
-algebra is understood from the context. It is said that a is Cuntz-equivalent to b, denoted by
![]() $a\sim b$
, if
$a\sim b$
, if
![]() $a\precsim b$
and
$a\precsim b$
and
![]() $b \precsim a$
. The Cuntz semigroup is given by
$b \precsim a$
. The Cuntz semigroup is given by
![]() $\mathrm {Cu}(A) = (A \otimes \mathbb {K})_+ / \sim $
equipped with orthogonal addition and order given by Cuntz subequivalence. The equivalence class of
$\mathrm {Cu}(A) = (A \otimes \mathbb {K})_+ / \sim $
equipped with orthogonal addition and order given by Cuntz subequivalence. The equivalence class of
![]() $a\in (A \otimes \mathbb {K})_+$
in
$a\in (A \otimes \mathbb {K})_+$
in
![]() $\mathrm {Cu}(A)$
is denoted by
$\mathrm {Cu}(A)$
is denoted by
![]() $\langle a \rangle $
. We refer to reader to [Reference Ara, Perera and Toms6, Section 2] for a more comprehensive review of the basic construction of the Cuntz semigroup.
$\langle a \rangle $
. We refer to reader to [Reference Ara, Perera and Toms6, Section 2] for a more comprehensive review of the basic construction of the Cuntz semigroup.
The Cuntz semigroup
![]() $\mathrm {Cu}(A)$
is called almost unperforated if
$\mathrm {Cu}(A)$
is called almost unperforated if
![]() $\langle a \rangle \leq \langle b \rangle $
holds whenever
$\langle a \rangle \leq \langle b \rangle $
holds whenever
![]() $\langle a \rangle , \langle b \rangle \in \mathrm {Cu}(A)$
satisfy
$\langle a \rangle , \langle b \rangle \in \mathrm {Cu}(A)$
satisfy
![]() $(k+1)\langle a \rangle \leq k \langle b \rangle $
for some
$(k+1)\langle a \rangle \leq k \langle b \rangle $
for some
![]() $k\in \mathbb {N}$
. For simplicity, we will simply say quasitrace instead of lower semicontinuous
$k\in \mathbb {N}$
. For simplicity, we will simply say quasitrace instead of lower semicontinuous
![]() $2$
-quasitrace (see [Reference Blanchard and Kirchberg8, Definition 2.22]). Any quasitrace on A extends uniquely to the quasitrace
$2$
-quasitrace (see [Reference Blanchard and Kirchberg8, Definition 2.22]). Any quasitrace on A extends uniquely to the quasitrace
![]() $\overline {\tau }:=\tau \otimes \mathrm {Tr}$
on
$\overline {\tau }:=\tau \otimes \mathrm {Tr}$
on
![]() $A\otimes \mathbb {K}$
by [Reference Blanchard and Kirchberg8, Remark 2.27]. The dimension function
$A\otimes \mathbb {K}$
by [Reference Blanchard and Kirchberg8, Remark 2.27]. The dimension function
![]() $d_{\tau }: (A\otimes \mathbb {K})_+ \to [0,\infty ]$
associated with
$d_{\tau }: (A\otimes \mathbb {K})_+ \to [0,\infty ]$
associated with
![]() $\tau $
is given by
$\tau $
is given by
![]() $d_{\tau } (a) = \lim _{n \to \infty } \overline {\tau }(a^{1/n})$
. This dimension function induces a well-defined functional on
$d_{\tau } (a) = \lim _{n \to \infty } \overline {\tau }(a^{1/n})$
. This dimension function induces a well-defined functional on
![]() $\mathrm {Cu}(A)$
.
$\mathrm {Cu}(A)$
.
It is said that A has strict comparison if
![]() $\langle a \rangle \leq \langle b\rangle $
holds whenever
$\langle a \rangle \leq \langle b\rangle $
holds whenever
![]() $d_{\tau }(\langle a \rangle )< d_{\tau }(\langle b \rangle )$
for every quasitrace
$d_{\tau }(\langle a \rangle )< d_{\tau }(\langle b \rangle )$
for every quasitrace
![]() $\tau $
on A with
$\tau $
on A with
![]() $d_{\tau } (\langle b \rangle )>0$
. If A is simple, then
$d_{\tau } (\langle b \rangle )>0$
. If A is simple, then
![]() $\mathrm {Cu}(A)$
is almost unperforated if and only if A has strict comparison (see [Reference Antoine, Perera and Thiel3, Proposition 5.2.20] or [Reference Thiel54, Remark 9.2(3)]).
$\mathrm {Cu}(A)$
is almost unperforated if and only if A has strict comparison (see [Reference Antoine, Perera and Thiel3, Proposition 5.2.20] or [Reference Thiel54, Remark 9.2(3)]).
We finish this subsection with the following definition.
Definition 2.1 [Reference Antoine, Perera and Thiel3, Definition 5.3.1]
Let
![]() $x,y \in \mathrm {Cu}(A)$
. It is said that x is way-below y, denoted
$x,y \in \mathrm {Cu}(A)$
. It is said that x is way-below y, denoted
![]() $x \ll y$
, if whenever
$x \ll y$
, if whenever
![]() $( y_n )_{n\in \mathbb {N}}$
is an increasing sequence with
$( y_n )_{n\in \mathbb {N}}$
is an increasing sequence with
![]() $y \leq \sup _{n \in \mathbb {N}} y_n$
, then there is some
$y \leq \sup _{n \in \mathbb {N}} y_n$
, then there is some
![]() $n \in \mathbb {N}$
such that
$n \in \mathbb {N}$
such that
![]() $x \leq y_n$
. An element
$x \leq y_n$
. An element
![]() $y \in \mathrm {Cu}(A)$
is soft if for any
$y \in \mathrm {Cu}(A)$
is soft if for any
![]() $x \in \mathrm {Cu}(B)$
such that
$x \in \mathrm {Cu}(B)$
such that
![]() $x \ll y$
there is some
$x \ll y$
there is some
![]() $k:=k(x) \in \mathbb {N}$
such that
$k:=k(x) \in \mathbb {N}$
such that
![]() $(k+1) x \leq ky$
.
$(k+1) x \leq ky$
.
2.4 Generalized limit traces
A trace
![]() $\tau $
on
$\tau $
on
![]() $A_{\omega }$
is called a limit trace if there is a sequence of tracial states
$A_{\omega }$
is called a limit trace if there is a sequence of tracial states
![]() $(\tau _n)_{n \in \mathbb {N} }$
on A such that
$(\tau _n)_{n \in \mathbb {N} }$
on A such that
![]() $\tau ((a_n)_{n\in \mathbb {N} }) = \lim _{n \to \omega } \tau _n(a_n)$
. Such tracial states on
$\tau ((a_n)_{n\in \mathbb {N} }) = \lim _{n \to \omega } \tau _n(a_n)$
. Such tracial states on
![]() $A_{\omega }$
capture enough about the global tracial information when A is unital, but become too restrictive when A has unbounded traces. In the general non-unital case, it becomes more appropriate to study the following class of traces.
$A_{\omega }$
capture enough about the global tracial information when A is unital, but become too restrictive when A has unbounded traces. In the general non-unital case, it becomes more appropriate to study the following class of traces.
Definition 2.2 [Reference Szabó53, Definition 2.1]
Let
![]() $\omega $
be a free ultrafilter on
$\omega $
be a free ultrafilter on
![]() $\mathbb {N}$
. For a sequence of lower semicontinuous traces
$\mathbb {N}$
. For a sequence of lower semicontinuous traces
![]() $(\tau _n)$
on A, one defines a lower semicontinuous trace
$(\tau _n)$
on A, one defines a lower semicontinuous trace
![]() $\tau : \ell ^{\infty } (A)_+ \to [0, \infty ]$
by
$\tau : \ell ^{\infty } (A)_+ \to [0, \infty ]$
by
This trace induces a lower semicontinuous trace on
![]() $A_{\omega }$
. Traces of this form on
$A_{\omega }$
. Traces of this form on
![]() $A_{\omega }$
are called generalized limit traces. The set of all generalized limit traces on
$A_{\omega }$
are called generalized limit traces. The set of all generalized limit traces on
![]() $A_{\omega }$
will be denoted by
$A_{\omega }$
will be denoted by
![]() $T_{\omega }^+(A)$
.
$T_{\omega }^+(A)$
.
Given a generalized limit trace
![]() $\tau $
on
$\tau $
on
![]() $A_{\omega }$
and
$A_{\omega }$
and
![]() $a\in A_+$
, the map
$a\in A_+$
, the map
![]() $\tau _a: (A_{\omega } \cap A')_+ \to [0, \infty ], x \mapsto \tau (ax)$
yields a trace that satisfies
$\tau _a: (A_{\omega } \cap A')_+ \to [0, \infty ], x \mapsto \tau (ax)$
yields a trace that satisfies
![]() $\tau _a (x) \leq \tau (a)\|x\|$
for
$\tau _a (x) \leq \tau (a)\|x\|$
for
![]() $x \in (A_{\omega } \cap A')_+$
. It actually extends to a positive tracial functional on
$x \in (A_{\omega } \cap A')_+$
. It actually extends to a positive tracial functional on
![]() $A_{\omega } \cap A'$
with norm
$A_{\omega } \cap A'$
with norm
![]() $\|\tau _a\|=\tau (a)$
if
$\|\tau _a\|=\tau (a)$
if
![]() $\tau (a)<\infty $
. Moreover, this induces a trace on
$\tau (a)<\infty $
. Moreover, this induces a trace on
![]() $F_{\omega }(A)$
, which we will also denote by
$F_{\omega }(A)$
, which we will also denote by
![]() $\tau _a$
. We refer the reader to [Reference Szabó53, Remark 2.3] for details.
$\tau _a$
. We refer the reader to [Reference Szabó53, Remark 2.3] for details.
Lemma 2.3 (cf. [Reference Castillejos and Evington12, Proposition 2.3])
Let A be an algebraically simple
![]() $\sigma $
-unital
$\sigma $
-unital
![]() $\mathrm {C}^*$
-algebra with
$\mathrm {C}^*$
-algebra with
![]() $T^+(A) \neq \{0,\infty \}$
. If a generalized limit trace on
$T^+(A) \neq \{0,\infty \}$
. If a generalized limit trace on
![]() $A_{\omega }$
is finite on some nonzero positive element of A, then it is a constant multiple of a limit trace.
$A_{\omega }$
is finite on some nonzero positive element of A, then it is a constant multiple of a limit trace.
Proof Since A is algebraically simple, all nontrivial lower semicontinuous traces on A are bounded and extend to positive tracial functionals. The same proof of [Reference Castillejos and Evington11, Proposition 2.3] remains valid except we replace compactness of
![]() $T(A)$
with [Reference Tikuisis55, Proposition 2.5] in order to obtain
$T(A)$
with [Reference Tikuisis55, Proposition 2.5] in order to obtain
![]() $\inf _{\sigma \in T(A)} \sigma (a)> 0$
for some nonzero
$\inf _{\sigma \in T(A)} \sigma (a)> 0$
for some nonzero
![]() $a \in A_+$
.
$a \in A_+$
.
2.5 Uniform McDuff property for non-unital
 $\mathrm {C}^*$
-algebras
$\mathrm {C}^*$
-algebras
We now present a non-unital version of the uniform McDuff property, which was defined in [Reference Castillejos, Evington, Tikuisis and White13, Definition 4.2] for
![]() $\mathrm {C}^*$
-algebras with compact tracial state space. As explained in [Reference Castillejos, Evington, Tikuisis and White13, Remark 4.3], the uniform McDuff property is equivalent to the existence of a c.p.c. order zero map
$\mathrm {C}^*$
-algebras with compact tracial state space. As explained in [Reference Castillejos, Evington, Tikuisis and White13, Remark 4.3], the uniform McDuff property is equivalent to the existence of a c.p.c. order zero map
![]() $\varphi : M_n(\mathbb {C}) \to A_{\omega } \cap A'$
such that
$\varphi : M_n(\mathbb {C}) \to A_{\omega } \cap A'$
such that
![]() $\tau ( \varphi (1_{M_n})) =1$
for any limit trace
$\tau ( \varphi (1_{M_n})) =1$
for any limit trace
![]() $\tau $
on
$\tau $
on
![]() $A_{\omega }$
; such maps have been called (uniformly) tracially large. We also state here a version of such maps in the general non-unital case.
$A_{\omega }$
; such maps have been called (uniformly) tracially large. We also state here a version of such maps in the general non-unital case.
Definition 2.4 Let A and B be
![]() $\mathrm {C}^*$
-algebras with B unital and A separable simple and
$\mathrm {C}^*$
-algebras with B unital and A separable simple and
![]() $T^+(A)\neq \{0,\infty \}$
. A c.p.c. order zero map
$T^+(A)\neq \{0,\infty \}$
. A c.p.c. order zero map
![]() $\varphi : B \to F_{\omega }(A)$
is tracially large if
$\varphi : B \to F_{\omega }(A)$
is tracially large if
![]() $\tau _a (\varphi (1)) = \tau (a)$
for all (or any) nonzero positive element
$\tau _a (\varphi (1)) = \tau (a)$
for all (or any) nonzero positive element
![]() $a \in \mathrm {Ped}(A)$
and
$a \in \mathrm {Ped}(A)$
and
![]() $\tau \in T^+_{\omega }(A)$
with
$\tau \in T^+_{\omega }(A)$
with
![]() $\tau (a) < \infty $
.Footnote
2
$\tau (a) < \infty $
.Footnote
2
We say that a separable, simple
![]() $\mathrm {C}^*$
-algebra A with
$\mathrm {C}^*$
-algebra A with
![]() $T^+(A)\neq \{0,\infty \}$
is uniformly McDuff if for every
$T^+(A)\neq \{0,\infty \}$
is uniformly McDuff if for every
![]() $n\in \mathbb {N}$
there is a tracially large order zero map
$n\in \mathbb {N}$
there is a tracially large order zero map
![]() $\varphi : M_n(\mathbb {C}) \to F_{\omega }(A)$
.
$\varphi : M_n(\mathbb {C}) \to F_{\omega }(A)$
.
As in [Reference Castillejos and Evington12, Proposition 2.6(ii)], the notion introduced here agrees with Definition 4.2 of [Reference Castillejos, Evington, Tikuisis and White13] if every
![]() $\tau \in T^+(A)\setminus \{\infty \}$
is bounded and the tracial state space is compact and nonempty. One may, hence, view the above as some kind of stabilized version of the previously defined notion of uniform McDuffness.
$\tau \in T^+(A)\setminus \{\infty \}$
is bounded and the tracial state space is compact and nonempty. One may, hence, view the above as some kind of stabilized version of the previously defined notion of uniform McDuffness.
Since stably isomorphic
![]() $\mathrm {C}^*$
-algebras have isomorphic central sequence algebras, it is reasonable to expect that the uniform McDuff property is also preserved. In order to prove this, one has to check how the stable isomorphism is transforming the traces of the form
$\mathrm {C}^*$
-algebras have isomorphic central sequence algebras, it is reasonable to expect that the uniform McDuff property is also preserved. In order to prove this, one has to check how the stable isomorphism is transforming the traces of the form
![]() $\tau _a$
with
$\tau _a$
with
![]() $a \in \mathrm {Ped}(A)$
and
$a \in \mathrm {Ped}(A)$
and
![]() $\tau \in T_{\omega }^+(A)$
.
$\tau \in T_{\omega }^+(A)$
.
Proposition 2.5 The uniform McDuff property is preserved under stable isomorphism.
Proof By [Reference Pedersen45, Theorem 1.4], any isomorphism between two
![]() $\mathrm {C}^*$
-algebras restricts to an isomorphism between their Pedersen ideals. If we combine this with [Reference Castillejos and Evington12, Proposition 2.8], it follows directly that the uniform McDuff property is preserved under genuine isomorphism. Therefore, given a separable simple
$\mathrm {C}^*$
-algebras restricts to an isomorphism between their Pedersen ideals. If we combine this with [Reference Castillejos and Evington12, Proposition 2.8], it follows directly that the uniform McDuff property is preserved under genuine isomorphism. Therefore, given a separable simple
![]() $\mathrm {C}^*$
-algebra A with
$\mathrm {C}^*$
-algebra A with
![]() $T^+(A)\neq \{0,\infty \}$
, it is enough to check that A is uniformly McDuff if and only if
$T^+(A)\neq \{0,\infty \}$
, it is enough to check that A is uniformly McDuff if and only if
![]() $A \otimes \mathbb {K}$
is uniformly McDuff.
$A \otimes \mathbb {K}$
is uniformly McDuff.
Consider
![]() $m\in \mathbb {N}$
and suppose
$m\in \mathbb {N}$
and suppose
![]() $\varphi : M_m(\mathbb {C}) \to F_{\omega } (A)$
is any completely positive contractive order zero map, which by [Reference Winter59, Proposition 1.2.4] can be represented by a sequence of order zero maps
$\varphi : M_m(\mathbb {C}) \to F_{\omega } (A)$
is any completely positive contractive order zero map, which by [Reference Winter59, Proposition 1.2.4] can be represented by a sequence of order zero maps
![]() $\varphi _n: M_m(\mathbb {C})\to A$
. Let
$\varphi _n: M_m(\mathbb {C})\to A$
. Let
![]() $\Psi : A_{\omega } \to (A\otimes \mathbb {K})_{\omega }$
be given by
$\Psi : A_{\omega } \to (A\otimes \mathbb {K})_{\omega }$
be given by
![]() $(a_n)_{n \in \mathbb {N}} \mapsto (a_n \otimes (\sum _{i=1}^n e_{ii}) )_{n \in \mathbb {N}}$
. By [Reference Castillejos and Evington12, Lemma 1.3] (which goes back to [Reference Kirchberg32]),
$(a_n)_{n \in \mathbb {N}} \mapsto (a_n \otimes (\sum _{i=1}^n e_{ii}) )_{n \in \mathbb {N}}$
. By [Reference Castillejos and Evington12, Lemma 1.3] (which goes back to [Reference Kirchberg32]),
![]() $\Psi $
induces an isomorphism
$\Psi $
induces an isomorphism
![]() $\bar {\Psi }: F_{\omega }(A) \to F_{\omega } (A \otimes \mathbb {K})$
. Consider a generalized limit trace
$\bar {\Psi }: F_{\omega }(A) \to F_{\omega } (A \otimes \mathbb {K})$
. Consider a generalized limit trace
![]() $\sigma \in T^+_{\omega }(A\otimes \mathbb {K})$
. This trace is induced by a sequence
$\sigma \in T^+_{\omega }(A\otimes \mathbb {K})$
. This trace is induced by a sequence
![]() $(\tau _n \otimes \mathrm {Tr})_{n \in \mathbb {N}}$
where
$(\tau _n \otimes \mathrm {Tr})_{n \in \mathbb {N}}$
where
![]() $\tau _n \in T^+(A)$
. Let
$\tau _n \in T^+(A)$
. Let
![]() $\tau $
be the generalized limit trace on
$\tau $
be the generalized limit trace on
![]() $A_{\omega }$
induced by the sequence
$A_{\omega }$
induced by the sequence
![]() $(\tau _n)_{n \in \mathbb {N}}$
. Suppose
$(\tau _n)_{n \in \mathbb {N}}$
. Suppose
![]() $a\in \mathrm {Ped}(A)\setminus \{0\}$
is positive. Then we observe
$a\in \mathrm {Ped}(A)\setminus \{0\}$
is positive. Then we observe

Now
![]() $\varphi $
is tracially large if and only if
$\varphi $
is tracially large if and only if
![]() $\tau _a(\phi (1))=\tau (a)$
whenever
$\tau _a(\phi (1))=\tau (a)$
whenever
![]() $0<\tau (a)<\infty $
, and
$0<\tau (a)<\infty $
, and
![]() $\bar {\Psi }\circ \varphi $
is tracially large if and only if
$\bar {\Psi }\circ \varphi $
is tracially large if and only if
![]() $\sigma _{a\otimes e_{11}}(\bar {\Psi }(\varphi (1)))=\sigma (a\otimes e_{11})$
whenever
$\sigma _{a\otimes e_{11}}(\bar {\Psi }(\varphi (1)))=\sigma (a\otimes e_{11})$
whenever
![]() $0<\sigma (a\otimes e_{11})<\infty $
. Since by construction we always have
$0<\sigma (a\otimes e_{11})<\infty $
. Since by construction we always have
![]() $\tau (a)=\sigma (a\otimes e_{11})$
for the aforementioned assignment
$\tau (a)=\sigma (a\otimes e_{11})$
for the aforementioned assignment
![]() $\sigma \mapsto \tau $
, the computation above directly implies that
$\sigma \mapsto \tau $
, the computation above directly implies that
![]() $\varphi $
is tracially large if and only if
$\varphi $
is tracially large if and only if
![]() $\bar {\Psi }\circ \varphi $
is tracially large. Consequently, A is uniformly McDuff if and only if
$\bar {\Psi }\circ \varphi $
is tracially large. Consequently, A is uniformly McDuff if and only if
![]() $A \otimes \mathbb {K}$
is.
$A \otimes \mathbb {K}$
is.
Remark 2.6 If A is a separable simple exact
![]() ${\mathcal {Z}}$
-stable
${\mathcal {Z}}$
-stable
![]() $\mathrm {C}^*$
-algebra with
$\mathrm {C}^*$
-algebra with
![]() $T^+(A)\neq \{0,\infty \}$
, then it is uniformly McDuff. Indeed, let us first assume that every nontrivial trace on A is a multiple of a tracial state and that
$T^+(A)\neq \{0,\infty \}$
, then it is uniformly McDuff. Indeed, let us first assume that every nontrivial trace on A is a multiple of a tracial state and that
![]() $T(A)$
is compact. Let
$T(A)$
is compact. Let
![]() $n \in \mathbb {N}$
. By [Reference Castillejos, Evington, Tikuisis, White and Winter14, Proposition 2.3], there is an order zero map
$n \in \mathbb {N}$
. By [Reference Castillejos, Evington, Tikuisis, White and Winter14, Proposition 2.3], there is an order zero map
![]() $\varphi : M_n(\mathbb {C}) \to F_{\omega }(A)= A_{\omega } \cap A'$
such that
$\varphi : M_n(\mathbb {C}) \to F_{\omega }(A)= A_{\omega } \cap A'$
such that
![]() $\tau (\varphi (1)) = 1$
for all
$\tau (\varphi (1)) = 1$
for all
![]() $\tau \in T_{\omega } (A)$
. It follows that A is uniformly McDuff. We, hence, observe that the general case follows with the previous proposition and [Reference Castillejos and Evington11, Theorem 2.7].
$\tau \in T_{\omega } (A)$
. It follows that A is uniformly McDuff. We, hence, observe that the general case follows with the previous proposition and [Reference Castillejos and Evington11, Theorem 2.7].
In light of [Reference Castillejos, Evington, Tikuisis and White13, Theorem 4.6], it is natural to ask about the relation between the uniform McDuff property and the stabilized uniform property
![]() $\Gamma $
(see [Reference Castillejos and Evington12, Definition 2.5]). We can at least provide an answer to this question if we assume a regularity condition at the level of the Cuntz semigroup. (It is conceivable that, although our proof uses these assumptions, the statement may actually hold in greater generality.)
$\Gamma $
(see [Reference Castillejos and Evington12, Definition 2.5]). We can at least provide an answer to this question if we assume a regularity condition at the level of the Cuntz semigroup. (It is conceivable that, although our proof uses these assumptions, the statement may actually hold in greater generality.)
Proposition 2.7 Let A be a simple separable
![]() $\mathrm {C}^*$
-algebra with
$\mathrm {C}^*$
-algebra with
![]() $T^+(A)\neq \{0,\infty \}$
. If A is uniformly McDuff, then A has stabilized uniform property
$T^+(A)\neq \{0,\infty \}$
. If A is uniformly McDuff, then A has stabilized uniform property
![]() $\Gamma $
. The converse holds if A is nuclear and has either stable rank one or
$\Gamma $
. The converse holds if A is nuclear and has either stable rank one or
![]() $\mathrm {Cu}(A \otimes {\mathcal {Z}}) \cong \mathrm {Cu}(A)$
.
$\mathrm {Cu}(A \otimes {\mathcal {Z}}) \cong \mathrm {Cu}(A)$
.
Proof Suppose A is uniformly McDuff. Then, for any
![]() $n\in \mathbb {N}$
, there is a tracially large order zero map
$n\in \mathbb {N}$
, there is a tracially large order zero map
![]() $\varphi : M_n(\mathbb {C}) \to F_{\omega }(A)$
. It follows that the map
$\varphi : M_n(\mathbb {C}) \to F_{\omega }(A)$
. It follows that the map
![]() $x \mapsto \tau _a(\varphi (x))$
is a tracial functional on
$x \mapsto \tau _a(\varphi (x))$
is a tracial functional on
![]() $M_n(\mathbb {C})$
for any
$M_n(\mathbb {C})$
for any
![]() $a \in A_+$
and
$a \in A_+$
and
![]() $\tau \in T^+_{\omega }(A)$
with
$\tau \in T^+_{\omega }(A)$
with
![]() $\tau (a)<\infty $
. If
$\tau (a)<\infty $
. If
![]() $\mathrm {tr}$
denotes the normalized trace on
$\mathrm {tr}$
denotes the normalized trace on
![]() $M_n(\mathbb {C})$
, then
$M_n(\mathbb {C})$
, then
Observe that the last equality follows from the fact that
![]() $\varphi $
is tracially large. If we set
$\varphi $
is tracially large. If we set
![]() $f_i = \varphi (e_{ii})$
, then the previous equation shows
$f_i = \varphi (e_{ii})$
, then the previous equation shows
![]() $\tau _a (f_i) = \frac {1}{n}\tau (a)$
for any
$\tau _a (f_i) = \frac {1}{n}\tau (a)$
for any
![]() $a \in A_+$
and
$a \in A_+$
and
![]() $\tau \in T^+_{\omega }(A)$
with
$\tau \in T^+_{\omega }(A)$
with
![]() $\tau (a)<\infty $
. Hence, A has stabilized uniform property
$\tau (a)<\infty $
. Hence, A has stabilized uniform property
![]() $\Gamma $
.
$\Gamma $
.
For the converse implication, we suppose that A is nuclear and has either stable rank one or satisfies
![]() $\mathrm {Cu}(A \otimes {\mathcal {Z}}) \cong \mathrm {Cu}(A)$
. By [Reference Castillejos and Evington11, Proposition 2.4], A is either stably projectionless or stably isomorphic to a unital
$\mathrm {Cu}(A \otimes {\mathcal {Z}}) \cong \mathrm {Cu}(A)$
. By [Reference Castillejos and Evington11, Proposition 2.4], A is either stably projectionless or stably isomorphic to a unital
![]() $\mathrm {C}^*$
-algebra. In the stably projectionless case, A is also stably isomorphic to a
$\mathrm {C}^*$
-algebra. In the stably projectionless case, A is also stably isomorphic to a
![]() $\mathrm {C}^*$
-algebra B with nonempty compact tracial state space and without unbounded traces by [Reference Castillejos and Evington12, Lemma 3.3] and the final observation in [Reference Castillejos and Evington12] (this uses the assumption that either
$\mathrm {C}^*$
-algebra B with nonempty compact tracial state space and without unbounded traces by [Reference Castillejos and Evington12, Lemma 3.3] and the final observation in [Reference Castillejos and Evington12] (this uses the assumption that either
![]() $\mathrm {Cu}(A) = \mathrm {Cu}(A \otimes {\mathcal {Z}})$
or A has stable rank one, respectively).
$\mathrm {Cu}(A) = \mathrm {Cu}(A \otimes {\mathcal {Z}})$
or A has stable rank one, respectively).
Since A is nonelementary, simple, separable, and nuclear, B is also nonelementary, simple, separable, and nuclear. By [Reference Castillejos, Evington, Tikuisis and White13, Theorem 4.6], B is uniformly McDuff if and only if B has uniform property
![]() $\Gamma $
. Then, since stabilized property
$\Gamma $
. Then, since stabilized property
![]() $\Gamma $
and the McDuff property are preserved under stable isomorphisms (see [Reference Castillejos and Evington12, Theorem 2.10 and Proposition 2.6] and Proposition 2.5), we deduce that A is uniformly McDuff if and only if A has stabilized uniform property
$\Gamma $
and the McDuff property are preserved under stable isomorphisms (see [Reference Castillejos and Evington12, Theorem 2.10 and Proposition 2.6] and Proposition 2.5), we deduce that A is uniformly McDuff if and only if A has stabilized uniform property
![]() $\Gamma $
.
$\Gamma $
.
3 Tracial
 ${\mathcal {Z}}$
-stability
${\mathcal {Z}}$
-stability
Let us begin by stating the general version of tracial
![]() ${\mathcal {Z}}$
-stability. This notion uses the idea of “tracial smallness” that can be traced back to [Reference Forough and Golestani20, Reference Hirshberg and Orovitz27, Reference Lin35, Reference Lin36, Reference Phillips46].
${\mathcal {Z}}$
-stability. This notion uses the idea of “tracial smallness” that can be traced back to [Reference Forough and Golestani20, Reference Hirshberg and Orovitz27, Reference Lin35, Reference Lin36, Reference Phillips46].
Definition 3.1 (see also [Reference Amini, Golestani, Jamali and Phillips1, Definition 3.6])
A simple
![]() $\mathrm {C}^*$
-algebra A is tracially
$\mathrm {C}^*$
-algebra A is tracially
![]() ${\mathcal {Z}}$
-stable if
${\mathcal {Z}}$
-stable if
![]() $A \neq \mathbb {C}$
and for any finite set
$A \neq \mathbb {C}$
and for any finite set
![]() $\mathfrak {F}\subseteq A$
,
$\mathfrak {F}\subseteq A$
,
![]() $\epsilon>0$
, nonzero positive elements
$\epsilon>0$
, nonzero positive elements
![]() $a, b \in A_+$
, and
$a, b \in A_+$
, and
![]() $n\in \mathbb {N}$
, there is a c.p.c. order zero map
$n\in \mathbb {N}$
, there is a c.p.c. order zero map
![]() $\varphi : M_n(\mathbb {C}) \to A$
such that
$\varphi : M_n(\mathbb {C}) \to A$
such that
Remark 3.2 When A is a unital
![]() $\mathrm {C}^*$
-algebra, it is straightforward to see that [Reference Hirshberg and Orovitz27, Definition 2.1] implies Definition 3.1. The converse implication follows from functional calculus of c.p.c. order zero maps. More precisely, we consider the map
$\mathrm {C}^*$
-algebra, it is straightforward to see that [Reference Hirshberg and Orovitz27, Definition 2.1] implies Definition 3.1. The converse implication follows from functional calculus of c.p.c. order zero maps. More precisely, we consider the map
![]() $f(\varphi )$
where f is a continuous function on
$f(\varphi )$
where f is a continuous function on
![]() $[0,1]$
given by
$[0,1]$
given by
 $$ \begin{align*} f(t):=\begin{cases} (1-\epsilon)^{-1}t, & \quad t \in [0,1-\epsilon], \\ 1, & \quad t \in [1-\epsilon,1]. \end{cases} \end{align*} $$
$$ \begin{align*} f(t):=\begin{cases} (1-\epsilon)^{-1}t, & \quad t \in [0,1-\epsilon], \\ 1, & \quad t \in [1-\epsilon,1]. \end{cases} \end{align*} $$
This order zero map satisfies that
![]() $1-f(\varphi )(1) \sim (1-\varphi (1)-\epsilon )_+$
(see the proof of [Reference Archey, Buck and Phillips7, Lemma 2.8]).
$1-f(\varphi )(1) \sim (1-\varphi (1)-\epsilon )_+$
(see the proof of [Reference Archey, Buck and Phillips7, Lemma 2.8]).
Remark 3.3
-
(a) We also note that in principle we allow
 $\varphi $
to be the zero map in order to consider purely infinite simple
$\varphi $
to be the zero map in order to consider purely infinite simple
 $\mathrm {C}^*$
-algebras as tracially
$\mathrm {C}^*$
-algebras as tracially
 ${\mathcal {Z}}$
-stable (see also [Reference Kirchberg and Rørdam33, Proposition 3.5(ii)]). This has the one downside that it would a priori also include
${\mathcal {Z}}$
-stable (see also [Reference Kirchberg and Rørdam33, Proposition 3.5(ii)]). This has the one downside that it would a priori also include
 $\mathbb {C}$
as an example, which is why we exclude this specific case in the definition.
$\mathbb {C}$
as an example, which is why we exclude this specific case in the definition. -
(b) We can furthermore observe that simple
 $\mathrm {C}^*$
-algebras cannot be tracially
$\mathrm {C}^*$
-algebras cannot be tracially
 ${\mathcal {Z}}$
-stable if they are elementary, i.e., of type I. Indeed, suppose
${\mathcal {Z}}$
-stable if they are elementary, i.e., of type I. Indeed, suppose
 $A=\mathbb K(\mathcal H)$
for a Hilbert space of dimension at least 2. Let
$A=\mathbb K(\mathcal H)$
for a Hilbert space of dimension at least 2. Let
 $p_1, p_2\in A$
be two orthogonal rank one projections, and let
$p_1, p_2\in A$
be two orthogonal rank one projections, and let
 $v\in A$
be a partial isometry with
$v\in A$
be a partial isometry with
 $v^*v=p_1$
and
$v^*v=p_1$
and
 $vv^*=p_2$
. If we consider
$vv^*=p_2$
. If we consider
 $a=p_1$
,
$a=p_1$
,
 $b=p_1+p_2$
, and
$b=p_1+p_2$
, and
 $\mathfrak F=\{v,v^*\}$
and choose a c.p.c. order zero map
$\mathfrak F=\{v,v^*\}$
and choose a c.p.c. order zero map
 $\varphi $
for
$\varphi $
for
 $n=2$
as in the definition of tracial
$n=2$
as in the definition of tracial
 ${\mathcal {Z}}$
-stability for small enough
${\mathcal {Z}}$
-stability for small enough
 $\epsilon $
, then we obtain a contradiction. This is because if
$\epsilon $
, then we obtain a contradiction. This is because if
 $x\in M_2(\mathbb C)$
is any contraction, then the operator
$x\in M_2(\mathbb C)$
is any contraction, then the operator
 $\varphi (x)$
not only leaves the two-dimensional subspace
$\varphi (x)$
not only leaves the two-dimensional subspace
 $(p_1+p_2)\mathcal H$
approximately invariant (as
$(p_1+p_2)\mathcal H$
approximately invariant (as
 $[\varphi (x),b]\approx 0$
), but
$[\varphi (x),b]\approx 0$
), but
 $\|[\varphi (x),\mathfrak F]\|\approx 0$
forces
$\|[\varphi (x),\mathfrak F]\|\approx 0$
forces
 $\varphi (x)$
to act like a constant multiple of the identity on this subspace. Considering the domain of
$\varphi (x)$
to act like a constant multiple of the identity on this subspace. Considering the domain of
 $\varphi $
, it can, hence, only be order zero if
$\varphi $
, it can, hence, only be order zero if
 $b\varphi (\cdot )b$
is close to the zero map. For sufficiently small
$b\varphi (\cdot )b$
is close to the zero map. For sufficiently small
 $\epsilon $
, this would yield
$\epsilon $
, this would yield
 $\frac 12(p_1+p_2)\leq (b(1_{\tilde {A}} - \varphi (1))b-\epsilon )_+ \precsim a=p_1$
, which is not possible.
$\frac 12(p_1+p_2)\leq (b(1_{\tilde {A}} - \varphi (1))b-\epsilon )_+ \precsim a=p_1$
, which is not possible.
The following is rather straightforward.
Lemma 3.4 Let A be a simple
![]() $\mathrm {C}^*$
-algebra with
$\mathrm {C}^*$
-algebra with
![]() $A\neq \mathbb C$
. Let
$A\neq \mathbb C$
. Let
![]() $\mathcal S\subseteq A_+$
be any subset containing an approximate unit of contractions. Then A is tracially
$\mathcal S\subseteq A_+$
be any subset containing an approximate unit of contractions. Then A is tracially
![]() ${\mathcal {Z}}$
-stable if and only if for any finite set
${\mathcal {Z}}$
-stable if and only if for any finite set
![]() $\mathfrak {F}\subseteq A$
,
$\mathfrak {F}\subseteq A$
,
![]() $\epsilon>0$
, nonzero positive contraction
$\epsilon>0$
, nonzero positive contraction
![]() $a \in A$
,
$a \in A$
,
![]() $b\in \mathcal S$
, and
$b\in \mathcal S$
, and
![]() $n\in \mathbb {N}$
, there is a c.p.c. order zero map
$n\in \mathbb {N}$
, there is a c.p.c. order zero map
![]() $\varphi : M_n(\mathbb {C}) \to A$
such that
$\varphi : M_n(\mathbb {C}) \to A$
such that
Proof The “only if” part is tautological. For the “if” part, let us fix an arbitrary tuple
![]() $(\mathfrak {F},\epsilon ,a,b,n)$
, in particular with some arbitrary element
$(\mathfrak {F},\epsilon ,a,b,n)$
, in particular with some arbitrary element
![]() $b\in A_+$
with norm one. By the property of
$b\in A_+$
with norm one. By the property of
![]() $\mathcal S$
, we may choose a positive contraction
$\mathcal S$
, we may choose a positive contraction
![]() $h\in \mathcal S$
with
$h\in \mathcal S$
with
![]() $\|b-bh\|<\epsilon /4$
. By assumption, we can find a c.p.c. order zero map
$\|b-bh\|<\epsilon /4$
. By assumption, we can find a c.p.c. order zero map
![]() $\varphi : M_n(\mathbb {C}) \to A$
such that
$\varphi : M_n(\mathbb {C}) \to A$
such that
Using the well-known [Reference Kirchberg and Rørdam34, Lemma 2.2], we observe
 $$\begin{align*} \begin{array}{ccl} (b(1_{\tilde{A}} - \varphi(1))b-\epsilon)_+ &\precsim& (bh(1_{\tilde{A}} - \varphi(1))hb-\frac{\epsilon}{2})_+ \\ &\precsim& b(h(1_{\tilde{A}} - \varphi(1))h-\frac{\epsilon}{2})_+ b \\ &\precsim& (h(1_{\tilde{A}} - \varphi(1))h-\frac{\epsilon}{2})_+ \ \precsim \ a. \end{array}\\[-33pt] \end{align*}$$
$$\begin{align*} \begin{array}{ccl} (b(1_{\tilde{A}} - \varphi(1))b-\epsilon)_+ &\precsim& (bh(1_{\tilde{A}} - \varphi(1))hb-\frac{\epsilon}{2})_+ \\ &\precsim& b(h(1_{\tilde{A}} - \varphi(1))h-\frac{\epsilon}{2})_+ b \\ &\precsim& (h(1_{\tilde{A}} - \varphi(1))h-\frac{\epsilon}{2})_+ \ \precsim \ a. \end{array}\\[-33pt] \end{align*}$$
Proposition 3.5 Let A be a simple
![]() $\mathrm {C}^*$
-algebra with
$\mathrm {C}^*$
-algebra with
![]() $A\neq \mathbb C$
. Then A is tracially
$A\neq \mathbb C$
. Then A is tracially
![]() ${\mathcal {Z}}$
-stable if and only if for any
${\mathcal {Z}}$
-stable if and only if for any
![]() $n \in \mathbb {N}$
, any separable
$n \in \mathbb {N}$
, any separable
![]() $\mathrm {C}^*$
-subalgebra
$\mathrm {C}^*$
-subalgebra
![]() $D\subseteq A$
, and any positive element
$D\subseteq A$
, and any positive element
![]() $a \in A_{\omega }$
of norm one, there exist a c.p.c. order zero map
$a \in A_{\omega }$
of norm one, there exist a c.p.c. order zero map
![]() $\varphi :M_n(\mathbb {C}) \to A_{\omega } \cap D'$
and a contraction
$\varphi :M_n(\mathbb {C}) \to A_{\omega } \cap D'$
and a contraction
![]() $x\in A_{\omega }$
such that
$x\in A_{\omega }$
such that
Proof Suppose that A is tracially
![]() ${\mathcal {Z}}$
-stable. Let
${\mathcal {Z}}$
-stable. Let
![]() $(a_k)_{k\in \mathbb {N}}$
be a sequence of positive elements of norm one representing
$(a_k)_{k\in \mathbb {N}}$
be a sequence of positive elements of norm one representing
![]() $a\in A_{\omega }$
and fix
$a\in A_{\omega }$
and fix
![]() $n \in \mathbb {N}$
. By employing functional calculus, we may perturb
$n \in \mathbb {N}$
. By employing functional calculus, we may perturb
![]() $(a_n)_{n\in \mathbb {N}}$
by a null sequence and assume without loss of generality that there exists another sequence of norm one positive elements
$(a_n)_{n\in \mathbb {N}}$
by a null sequence and assume without loss of generality that there exists another sequence of norm one positive elements
![]() $(d_k)_{k\in \mathbb {N}}$
with
$(d_k)_{k\in \mathbb {N}}$
with
![]() $d_ka_k=d_k$
for all
$d_ka_k=d_k$
for all
![]() $k\in \mathbb {N}$
. We choose a countable increasing approximate unit
$k\in \mathbb {N}$
. We choose a countable increasing approximate unit
![]() $\{e_k\}_{k\in \mathbb {N}}$
in
$\{e_k\}_{k\in \mathbb {N}}$
in
![]() $D_+$
, and let
$D_+$
, and let
![]() $e\in D_{\omega }\subset A_{\omega }$
be its induced element. Let
$e\in D_{\omega }\subset A_{\omega }$
be its induced element. Let
![]() $\mathfrak {F}_k \subset D$
be an increasing sequence of finite subsets with dense union.
$\mathfrak {F}_k \subset D$
be an increasing sequence of finite subsets with dense union.
Using the hypothesis, we can find a sequence of c.p.c. order zero maps
![]() $\varphi _k: M_n(\mathbb {C}) \to A$
such that
$\varphi _k: M_n(\mathbb {C}) \to A$
such that
In particular, we may find a (possibly unbounded) sequence
![]() $r_k\in A$
satisfying
$r_k\in A$
satisfying
We see that the sequence
![]() $x_k=\sqrt {d_k}r_k$
satisfies
$x_k=\sqrt {d_k}r_k$
satisfies
![]() $\limsup _{k\to \infty } \|x_k\|\leq 1$
, so we obtain a contraction
$\limsup _{k\to \infty } \|x_k\|\leq 1$
, so we obtain a contraction
![]() $x\in A_{\omega }$
induced by this sequence. Let
$x\in A_{\omega }$
induced by this sequence. Let
![]() $\varphi : M_n(\mathbb {C}) \to A_{\omega }$
be the sequence induced by
$\varphi : M_n(\mathbb {C}) \to A_{\omega }$
be the sequence induced by
![]() $(\varphi _k)$
. Clearly,
$(\varphi _k)$
. Clearly,
![]() $\varphi $
is a c.p.c. order zero map, and by construction, the image of
$\varphi $
is a c.p.c. order zero map, and by construction, the image of
![]() $\varphi $
is actually in the relative commutant
$\varphi $
is actually in the relative commutant
![]() $A_{\omega } \cap D'$
. Furthermore, we have arranged that
$A_{\omega } \cap D'$
. Furthermore, we have arranged that
Since e acts like a unit on elements of D, we see that this implies the required condition
![]() $x^*x-( 1_{\tilde {A}_{\omega }} - \varphi (1))\in \tilde {A}_{\omega }\cap D^{\perp }$
.
$x^*x-( 1_{\tilde {A}_{\omega }} - \varphi (1))\in \tilde {A}_{\omega }\cap D^{\perp }$
.
Conversely, let
![]() $\mathfrak {F} \subseteq A$
be a finite subset,
$\mathfrak {F} \subseteq A$
be a finite subset,
![]() $\epsilon> 0$
, and consider nonzero positive elements
$\epsilon> 0$
, and consider nonzero positive elements
![]() $a, b \in A$
, and any
$a, b \in A$
, and any
![]() $n\in \mathbb {N}$
. Let us assume without loss of generality that
$n\in \mathbb {N}$
. Let us assume without loss of generality that
![]() $\|a\|=1$
and
$\|a\|=1$
and
![]() $\mathfrak F = \mathfrak F^*$
. By the hypothesis, there is an order zero map
$\mathfrak F = \mathfrak F^*$
. By the hypothesis, there is an order zero map
![]() $\varphi : M_n(\mathbb {C}) \to A_{\omega } \cap \mathfrak F'$
and a contraction
$\varphi : M_n(\mathbb {C}) \to A_{\omega } \cap \mathfrak F'$
and a contraction
![]() $x\in A_{\omega }$
such that
$x\in A_{\omega }$
such that
![]() $ax=x$
and
$ax=x$
and
![]() $x^*x-(1_{\tilde {A}_{\omega }}-\varphi (1))\in \tilde {A}_{\omega }\cap \{b\}^{\perp }$
. A particular consequence of this is
$x^*x-(1_{\tilde {A}_{\omega }}-\varphi (1))\in \tilde {A}_{\omega }\cap \{b\}^{\perp }$
. A particular consequence of this is
![]() $bx^*axb=b(1_{\tilde {A}_{\omega }}-\varphi (1))b$
. By [Reference Winter59, Proposition 1.2.4], we can find a sequence of order zero maps
$bx^*axb=b(1_{\tilde {A}_{\omega }}-\varphi (1))b$
. By [Reference Winter59, Proposition 1.2.4], we can find a sequence of order zero maps
![]() $\varphi _k: M_n(\mathbb {C}) \to A$
that induces
$\varphi _k: M_n(\mathbb {C}) \to A$
that induces
![]() $\varphi $
. Likewise, choose a sequence of contractions
$\varphi $
. Likewise, choose a sequence of contractions
![]() $x_k\in A$
representing x. Then this leads to the limit behavior
$x_k\in A$
representing x. Then this leads to the limit behavior
Thus, there is
![]() $I\in \omega $
such that for all
$I\in \omega $
such that for all
![]() $k \in I$
, one has
$k \in I$
, one has
It follows that
![]() $(b(1_{\tilde {A}}-\varphi _k (1))b - \epsilon )_+ \precsim bx_k^* a x_kb \precsim a$
. Since the image of
$(b(1_{\tilde {A}}-\varphi _k (1))b - \epsilon )_+ \precsim bx_k^* a x_kb \precsim a$
. Since the image of
![]() $\varphi $
is in the relative commutant
$\varphi $
is in the relative commutant
![]() $A_{\omega } \cap \mathfrak F'$
, we can also assume that
$A_{\omega } \cap \mathfrak F'$
, we can also assume that
![]() $\|[\varphi _k, \mathfrak F]\|<\epsilon $
for suitably chosen k. This shows that A is tracially
$\|[\varphi _k, \mathfrak F]\|<\epsilon $
for suitably chosen k. This shows that A is tracially
![]() ${\mathcal {Z}}$
-stable.
${\mathcal {Z}}$
-stable.
We will now prove some permanence properties for tracial
![]() ${\mathcal {Z}}$
-stability.
${\mathcal {Z}}$
-stability.
Proposition 3.6 (see also [Reference Amini, Golestani, Jamali and Phillips1, Theorem 4.1])
Let A be a simple
![]() $\mathrm {C}^*$
-algebra, and suppose that
$\mathrm {C}^*$
-algebra, and suppose that
![]() $B\subseteq A$
is a hereditary
$B\subseteq A$
is a hereditary
![]() $\mathrm {C}^*$
-subalgebra. If A is tracially
$\mathrm {C}^*$
-subalgebra. If A is tracially
![]() ${\mathcal {Z}}$
-stable, then so is B.
${\mathcal {Z}}$
-stable, then so is B.
Proof Since A is tracially
![]() ${\mathcal {Z}}$
-stable, it cannot be of type I. Since A is also simple and B is hereditary, we may conclude
${\mathcal {Z}}$
-stable, it cannot be of type I. Since A is also simple and B is hereditary, we may conclude
![]() $B\neq \mathbb C$
. So it suffices to show that the condition in Proposition 3.5 passes from A to B. Let
$B\neq \mathbb C$
. So it suffices to show that the condition in Proposition 3.5 passes from A to B. Let
![]() $D\subseteq B$
be a separable
$D\subseteq B$
be a separable
![]() $\mathrm {C}^*$
-subalgebra, and let
$\mathrm {C}^*$
-subalgebra, and let
![]() $b\in B_{\omega }$
be a positive element of norm one. A standard application of the
$b\in B_{\omega }$
be a positive element of norm one. A standard application of the
![]() $\epsilon $
-test yields a positive norm one element
$\epsilon $
-test yields a positive norm one element
![]() $e\in B_{\omega }$
such that
$e\in B_{\omega }$
such that
![]() $ed=d=de$
for all
$ed=d=de$
for all
![]() $d\in D\cup \{b\}$
. Let
$d\in D\cup \{b\}$
. Let
![]() $n\in \mathbb {N}$
. Using that A is tracially
$n\in \mathbb {N}$
. Using that A is tracially
![]() ${\mathcal {Z}}$
-stable, we find a c.p.c. order zero map
${\mathcal {Z}}$
-stable, we find a c.p.c. order zero map
![]() $\psi : M_n(\mathbb C)\to A_{\omega }\cap D'\cap \{e\}'$
and a contraction
$\psi : M_n(\mathbb C)\to A_{\omega }\cap D'\cap \{e\}'$
and a contraction
![]() $x\in A_{\omega }$
such that
$x\in A_{\omega }$
such that
![]() $bx=x$
and
$bx=x$
and
in
![]() $(\tilde {A}_{\omega }\cap D')/(\tilde {A}_{\omega }\cap D^{\perp })$
. By these properties of
$(\tilde {A}_{\omega }\cap D')/(\tilde {A}_{\omega }\cap D^{\perp })$
. By these properties of
![]() $\psi $
and the fact that B is hereditary, we see that
$\psi $
and the fact that B is hereditary, we see that
![]() $\varphi =e\psi (\cdot )e: M_n(\mathbb C)\to B_{\omega }\cap D'$
is also c.p.c. order zero. Furthermore, we obtain the equality
$\varphi =e\psi (\cdot )e: M_n(\mathbb C)\to B_{\omega }\cap D'$
is also c.p.c. order zero. Furthermore, we obtain the equality
in
![]() $(\tilde {A}_{\omega } \cap D' )/ (\tilde {A}_{\omega } \cap D^{\perp })$
. Since clearly
$(\tilde {A}_{\omega } \cap D' )/ (\tilde {A}_{\omega } \cap D^{\perp })$
. Since clearly
![]() $bxe=xe$
, we have that
$bxe=xe$
, we have that
![]() $xe\in B_{\omega }$
is a contraction, and the equation from left to right actually holds in
$xe\in B_{\omega }$
is a contraction, and the equation from left to right actually holds in
![]() $(\tilde {B}_{\omega } \cap D')/(\tilde {B}_{\omega }\cap D^{\perp })$
. This finishes the proof.
$(\tilde {B}_{\omega } \cap D')/(\tilde {B}_{\omega }\cap D^{\perp })$
. This finishes the proof.
We now prove that tracial
![]() ${\mathcal {Z}}$
-stability passes to minimal tensor products with arbitrary simple
${\mathcal {Z}}$
-stability passes to minimal tensor products with arbitrary simple
![]() $\mathrm {C}^*$
-algebras. This observation in particular generalizes [Reference Hirshberg and Orovitz27, Lemma 2.4].
$\mathrm {C}^*$
-algebras. This observation in particular generalizes [Reference Hirshberg and Orovitz27, Lemma 2.4].
Proposition 3.7 (see also [Reference Amini, Golestani, Jamali and Phillips1, Theorem 5.1])
Let A and B be two simple
![]() $\mathrm {C}^*$
-algebras. If A is tracially
$\mathrm {C}^*$
-algebras. If A is tracially
![]() ${\mathcal {Z}}$
-stable, then so is the minimal tensor product
${\mathcal {Z}}$
-stable, then so is the minimal tensor product
![]() $A \otimes B$
.
$A \otimes B$
.
Proof Let
![]() $\mathfrak F_A\subset A$
and
$\mathfrak F_A\subset A$
and
![]() $\mathfrak F_B\subset B$
be finite sets of contractions. It suffices to check the condition in Definition 3.1 for sets of the form
$\mathfrak F_B\subset B$
be finite sets of contractions. It suffices to check the condition in Definition 3.1 for sets of the form
![]() $\mathfrak F=\{ a\otimes b\mid a\in \mathfrak F_A,\ b\in \mathfrak F_B\}$
. Let
$\mathfrak F=\{ a\otimes b\mid a\in \mathfrak F_A,\ b\in \mathfrak F_B\}$
. Let
![]() $g\in A\otimes B$
be a nonzero positive element, which will play the role of the element a in Definition 3.1. By Kirchberg’s slice lemma [Reference Rørdam and Størmer50, Lemma 4.1.9], we can find a pair of nonzero positive elements
$g\in A\otimes B$
be a nonzero positive element, which will play the role of the element a in Definition 3.1. By Kirchberg’s slice lemma [Reference Rørdam and Størmer50, Lemma 4.1.9], we can find a pair of nonzero positive elements
![]() $a_1\in A$
and
$a_1\in A$
and
![]() $b_0\in B$
with
$b_0\in B$
with
![]() $a_1\otimes b_0\precsim g$
. Appealing to Lemma 3.4, it suffices to check the condition in Definition 3.1 for elementary tensors of norm one positive contractions in place of arbitrary elements b as stated there.
$a_1\otimes b_0\precsim g$
. Appealing to Lemma 3.4, it suffices to check the condition in Definition 3.1 for elementary tensors of norm one positive contractions in place of arbitrary elements b as stated there.
Let
![]() $0<\epsilon <1$
and
$0<\epsilon <1$
and
![]() $n\in \mathbb {N}$
be given. Let
$n\in \mathbb {N}$
be given. Let
![]() $e\in A$
and
$e\in A$
and
![]() $f\in B$
be any pair of positive contractions of norm one. Since B is simple, we can find some natural number
$f\in B$
be any pair of positive contractions of norm one. Since B is simple, we can find some natural number
![]() $k\in \mathbb {N}$
with
$k\in \mathbb {N}$
with
Appealing to [Reference Hirshberg and Orovitz27, Lemma 2.3],Footnote
3
we find a nonzero positive contraction
![]() $a_0\in A$
with
$a_0\in A$
with
![]() $k\langle a_0\rangle \leq \langle a_1\rangle $
.
$k\langle a_0\rangle \leq \langle a_1\rangle $
.
Now use that A is tracially
![]() ${\mathcal {Z}}$
-stable and choose a c.p.c. order zero map
${\mathcal {Z}}$
-stable and choose a c.p.c. order zero map
![]() $\psi : M_n(\mathbb C)\to A$
satisfying
$\psi : M_n(\mathbb C)\to A$
satisfying
Let
![]() $s\in B$
be a positive contraction that satisfies
$s\in B$
be a positive contraction that satisfies
![]() $sx \approx _{\epsilon } x \approx _{\epsilon } xs$
for all
$sx \approx _{\epsilon } x \approx _{\epsilon } xs$
for all
![]() $x \in \mathfrak {F}_B \cup \{f\}$
. Then
$x \in \mathfrak {F}_B \cup \{f\}$
. Then
![]() $\varphi =\psi \otimes s: M_n(\mathbb C)\to A\otimes B$
is another c.p.c. order zero map that clearly satisfies
$\varphi =\psi \otimes s: M_n(\mathbb C)\to A\otimes B$
is another c.p.c. order zero map that clearly satisfies
![]() $\|[\varphi ,\mathfrak F]\|<3\epsilon $
. Then
$\|[\varphi ,\mathfrak F]\|<3\epsilon $
. Then
 $$\begin{align*}\begin{array}{cll} (e\otimes f)(1-\varphi(1))(e\otimes f) &\approx_{\epsilon}& (e\otimes f)(1_{\tilde{A}}\otimes s-\varphi(1))(e\otimes f) \\ &=& e(1-\psi(1))e\otimes fsf \\ &\approx_{\epsilon}& e(1-\psi(1))e\otimes f^2, \end{array} \end{align*}$$
$$\begin{align*}\begin{array}{cll} (e\otimes f)(1-\varphi(1))(e\otimes f) &\approx_{\epsilon}& (e\otimes f)(1_{\tilde{A}}\otimes s-\varphi(1))(e\otimes f) \\ &=& e(1-\psi(1))e\otimes fsf \\ &\approx_{\epsilon}& e(1-\psi(1))e\otimes f^2, \end{array} \end{align*}$$
and hence we observe (appealing again to [Reference Kirchberg and Rørdam34, Lemma 2.2]) that

This verifies the condition in Lemma 3.4 for
![]() $A\otimes B$
.
$A\otimes B$
.
A straightforward consequence of Propositions 3.6 and 3.7 is the following.
Corollary 3.8 (see also [Reference Amini, Golestani, Jamali and Phillips1, Proposition 4.11])
Let A be a simple
![]() $\mathrm {C}^*$
-algebra. Then A is tracially
$\mathrm {C}^*$
-algebra. Then A is tracially
![]() ${\mathcal {Z}}$
-stable if and only if
${\mathcal {Z}}$
-stable if and only if
![]() $A\otimes \mathbb {K}$
is tracially
$A\otimes \mathbb {K}$
is tracially
![]() ${\mathcal {Z}}$
-stable.
${\mathcal {Z}}$
-stable.
4 Strict comparison
We move now to show that simple tracially
![]() ${\mathcal {Z}}$
-stable
${\mathcal {Z}}$
-stable
![]() $\mathrm {C}^*$
-algebras have almost unperforated Cuntz semigroups. For this, we will mimic the original approach used by Hirshberg and Orovitz in [Reference Hirshberg and Orovitz27, Lemma 3.2]. The results appearing in this section were announced some years ago by the authors of [Reference Amini, Golestani, Jamali and Phillips1].
$\mathrm {C}^*$
-algebras have almost unperforated Cuntz semigroups. For this, we will mimic the original approach used by Hirshberg and Orovitz in [Reference Hirshberg and Orovitz27, Lemma 3.2]. The results appearing in this section were announced some years ago by the authors of [Reference Amini, Golestani, Jamali and Phillips1].
Lemma 4.1 (cf. [Reference Hirshberg and Orovitz27, Lemma 3.2])
Let A be a simple tracially
![]() $\mathcal {Z}$
-stable
$\mathcal {Z}$
-stable
![]() $\mathrm {C}^*$
-algebra. Let
$\mathrm {C}^*$
-algebra. Let
![]() $a,b\in A_+$
, and suppose that
$a,b\in A_+$
, and suppose that
![]() $0$
is an accumulation point of
$0$
is an accumulation point of
![]() $\sigma (b)$
. If
$\sigma (b)$
. If
![]() $k \langle a \rangle \leq k \langle b \rangle $
in
$k \langle a \rangle \leq k \langle b \rangle $
in
![]() $\mathrm {Cu}(A)$
for some
$\mathrm {Cu}(A)$
for some
![]() $k\in \mathbb {N}$
, then
$k\in \mathbb {N}$
, then
![]() $a\precsim b$
.
$a\precsim b$
.
Proof We will proceed as the original proof of [Reference Hirshberg and Orovitz27, Lemma 3.2] with some modifications. Since we have shown that hereditary subalgebras of A are tracially
![]() ${\mathcal {Z}}$
-stable, we may assume without loss of generality that A is
${\mathcal {Z}}$
-stable, we may assume without loss of generality that A is
![]() $\sigma $
-unital. Let us fix
$\sigma $
-unital. Let us fix
![]() $\epsilon>0$
. Without loss of generality, we may assume that a and b have norm equal to
$\epsilon>0$
. Without loss of generality, we may assume that a and b have norm equal to
![]() $1$
. Let
$1$
. Let
![]() $c=(c_{ij}) \in M_k(A)$
and
$c=(c_{ij}) \in M_k(A)$
and
![]() $\delta>0$
such that
$\delta>0$
such that
![]() $c((b-\delta )_+ \otimes 1_k) c^* = (a-\epsilon )_+ \otimes 1_k$
.
$c((b-\delta )_+ \otimes 1_k) c^* = (a-\epsilon )_+ \otimes 1_k$
.
Let
![]() $f \in C_0(0,1]$
be a nonnegative function of norm equal to
$f \in C_0(0,1]$
be a nonnegative function of norm equal to
![]() $1$
such that its support is contained in
$1$
such that its support is contained in
![]() $(0,\delta /2)$
. Set
$(0,\delta /2)$
. Set
![]() $d := f(b)$
, which is not zero since
$d := f(b)$
, which is not zero since
![]() $0$
is an accumulation point of
$0$
is an accumulation point of
![]() $\sigma (b)$
.
$\sigma (b)$
.
We fix
![]() $\mu>0$
. As in [Reference Hirshberg and Orovitz27, Lemma 3.2], we can assume that
$\mu>0$
. As in [Reference Hirshberg and Orovitz27, Lemma 3.2], we can assume that
![]() $c_{ij}d=0$
, and hence
$c_{ij}d=0$
, and hence
 $$ \begin{align} \sum_{r=1}^{k} c_{ir} (b-\delta)_+ c_{jr}^* = \begin{cases} (a-\epsilon)_+, & i=j, \\ 0, & i \neq j. \end{cases} \end{align} $$
$$ \begin{align} \sum_{r=1}^{k} c_{ir} (b-\delta)_+ c_{jr}^* = \begin{cases} (a-\epsilon)_+, & i=j, \\ 0, & i \neq j. \end{cases} \end{align} $$
Let
![]() $g \in C_0(0,1]$
such that
$g \in C_0(0,1]$
such that
![]() $g|_{[\frac {\mu }{7}, 1]} = 1$
and
$g|_{[\frac {\mu }{7}, 1]} = 1$
and
![]() $g(t)=\sqrt {7t/\mu }$
for
$g(t)=\sqrt {7t/\mu }$
for
![]() $t\in (0,\frac {\mu }{7}]$
. Let
$t\in (0,\frac {\mu }{7}]$
. Let
![]() $h \in C_0(0,1]$
be given by
$h \in C_0(0,1]$
be given by
![]() $h(t)=1-\sqrt {1-t}$
. Thus,
$h(t)=1-\sqrt {1-t}$
. Thus,
Set
![]() $\mathfrak {F} = \{(a-\epsilon )_+, (b-\delta )_+, (a-\varepsilon )^{1/2}_+\}\cup \{c_{ij}, c_{ij}(b-\delta )_+ c_{rs}^* \}_{i,j,r,s}$
. Since we assumed that A is
$\mathfrak {F} = \{(a-\epsilon )_+, (b-\delta )_+, (a-\varepsilon )^{1/2}_+\}\cup \{c_{ij}, c_{ij}(b-\delta )_+ c_{rs}^* \}_{i,j,r,s}$
. Since we assumed that A is
![]() $\sigma $
-unital, let
$\sigma $
-unital, let
![]() $(f_n)$
be a sequential increasing approximate unit of A satisfying
$(f_n)$
be a sequential increasing approximate unit of A satisfying
![]() $f_{n+1}f_n=f_n$
for all
$f_{n+1}f_n=f_n$
for all
![]() $n\geq 1$
. Find
$n\geq 1$
. Find
![]() $n \in \mathbb {N}$
large enough that satisfies
$n \in \mathbb {N}$
large enough that satisfies
Using tracial
![]() ${\mathcal {Z}}$
-stability, we find a c.p.c. order zero map
${\mathcal {Z}}$
-stability, we find a c.p.c. order zero map
![]() $\varphi : M_k(\mathbb {C}) \to A$
such that
$\varphi : M_k(\mathbb {C}) \to A$
such that
where
![]() $\eta>0$
is small enough so that
$\eta>0$
is small enough so that
The existence of such
![]() $\eta $
is guaranteed by [Reference Hirshberg and Orovitz27, Lemma 2.8].
$\eta $
is guaranteed by [Reference Hirshberg and Orovitz27, Lemma 2.8].
Let
![]() $m \geq n$
be such that
$m \geq n$
be such that
Set
 $$ \begin{align} a_1 & := f_m \varphi(1) (a-\epsilon)_+ f_m, \notag \\ a_2 & := (a-\epsilon)_+^{1/2} (f_m(1_{\tilde{A}}-\varphi(1))f_m-\eta)_+ (a-\epsilon)_+^{1/2}. \end{align} $$
$$ \begin{align} a_1 & := f_m \varphi(1) (a-\epsilon)_+ f_m, \notag \\ a_2 & := (a-\epsilon)_+^{1/2} (f_m(1_{\tilde{A}}-\varphi(1))f_m-\eta)_+ (a-\epsilon)_+^{1/2}. \end{align} $$
As
![]() $(f_n)$
is an increasing approximate unit and
$(f_n)$
is an increasing approximate unit and
![]() $m\geq n$
, it follows from (4.3) that
$m\geq n$
, it follows from (4.3) that
In particular,
Thus,
 $$ \begin{align} a_1 + a_2 &\overset{(4.9)}{\approx}_{\frac{2\mu}{15}} \varphi(1) (a-\epsilon)_+ + a_2 \notag \\ & \approx_{\eta} \varphi(1) (a-\epsilon)_+ + (a-\epsilon)_+^{1/2} f_m (1_{\tilde{A}}-\varphi(1))f_m (a-\epsilon)_+^{1/2} \notag \\ & \overset{(4.8)}{\approx}_{\frac{2\mu}{15}} \varphi(1) (a-\epsilon)_+ + (a-\epsilon)_+^{1/2} (1_{\tilde{A}}-\varphi(1)) (a-\epsilon)_+^{1/2} \notag \\ & \overset{(4.4)}{\approx}_{\frac{\mu}{15}} \varphi(1)(a-\epsilon)_+ + (1_{\tilde{A}}-\varphi(1))(a-\epsilon)_+ \notag \\ & = (a-\epsilon)_+. \end{align} $$
$$ \begin{align} a_1 + a_2 &\overset{(4.9)}{\approx}_{\frac{2\mu}{15}} \varphi(1) (a-\epsilon)_+ + a_2 \notag \\ & \approx_{\eta} \varphi(1) (a-\epsilon)_+ + (a-\epsilon)_+^{1/2} f_m (1_{\tilde{A}}-\varphi(1))f_m (a-\epsilon)_+^{1/2} \notag \\ & \overset{(4.8)}{\approx}_{\frac{2\mu}{15}} \varphi(1) (a-\epsilon)_+ + (a-\epsilon)_+^{1/2} (1_{\tilde{A}}-\varphi(1)) (a-\epsilon)_+^{1/2} \notag \\ & \overset{(4.4)}{\approx}_{\frac{\mu}{15}} \varphi(1)(a-\epsilon)_+ + (1_{\tilde{A}}-\varphi(1))(a-\epsilon)_+ \notag \\ & = (a-\epsilon)_+. \end{align} $$
As in the original proof [Reference Hirshberg and Orovitz27], we set
![]() $g_{ij} := g(\varphi )(e_{ij})$
,
$g_{ij} := g(\varphi )(e_{ij})$
,
![]() $\hat {c}_{ij} := \varphi ^{1/2}(1)g_{ij}c_{ij}$
and
$\hat {c}_{ij} := \varphi ^{1/2}(1)g_{ij}c_{ij}$
and
![]() $\hat {c}:= \sum _{i,j=1}^{k}\hat {c}_{ij}$
. Observe that
$\hat {c}:= \sum _{i,j=1}^{k}\hat {c}_{ij}$
. Observe that
 $$ \begin{align} g_{ij}g_{sr} = \begin{cases} g(\varphi)(1) \cdot g_{ir}, & j=s, \\ 0, & j \neq i. \end{cases} \end{align} $$
$$ \begin{align} g_{ij}g_{sr} = \begin{cases} g(\varphi)(1) \cdot g_{ir}, & j=s, \\ 0, & j \neq i. \end{cases} \end{align} $$
Then
 $$ \begin{align} \hat{c} (b-\delta)_+ \hat{c}^* & = \sum_{i,j,r,s=1}^{^k} \varphi^{1/2}(1)g_{ij}c_{ij} (b-\delta)_+ c_{rs}^* g_{sr} \varphi^{1/2}(1) \notag \\ & \overset{(4.5)}{\approx}_{\frac{\mu}{15}} \varphi(1) \sum_{i,j,r,s=1}^{^k} g_{ij}c_{ij} (b-\delta)_+ c_{rs}^* g_{sr} \notag \\ & \overset{(4.5)}{\approx}_{\frac{\mu}{15}} \varphi(1) \sum_{i,j,r,s=1}^{^k} g_{ij}g_{sr}c_{ij} (b-\delta)_+ c_{rs}^* \notag \\ & \overset{(4.11)}{=} \varphi(1) \cdot g(\varphi)(1) \sum_{i,j,r=1}^{^k} g_{ir}c_{ij} (b-\delta)_+ c_{rj}^* \notag \\ & \overset{(4.1)}{=} \varphi(1) \cdot g(\varphi)(1) \sum_{i=1}^{^k} g_{ii} \left( \sum_{j=1}^{k}c_{ij} (b-\delta)_+ c_{ij}^*\right) \notag \\ & \overset{(4.1)}{=} \varphi(1) \cdot g(\varphi)(1) \cdot g(\varphi)(1) \cdot (a-\epsilon)_+ \notag \\ & \overset{(4.2)}{\approx}_{\frac{\mu}{15}} \varphi(1) (a-\epsilon)_+ \notag \\ & \overset{(4.9)}{\approx}_{\frac{2\mu}{15}} a_1. \end{align} $$
$$ \begin{align} \hat{c} (b-\delta)_+ \hat{c}^* & = \sum_{i,j,r,s=1}^{^k} \varphi^{1/2}(1)g_{ij}c_{ij} (b-\delta)_+ c_{rs}^* g_{sr} \varphi^{1/2}(1) \notag \\ & \overset{(4.5)}{\approx}_{\frac{\mu}{15}} \varphi(1) \sum_{i,j,r,s=1}^{^k} g_{ij}c_{ij} (b-\delta)_+ c_{rs}^* g_{sr} \notag \\ & \overset{(4.5)}{\approx}_{\frac{\mu}{15}} \varphi(1) \sum_{i,j,r,s=1}^{^k} g_{ij}g_{sr}c_{ij} (b-\delta)_+ c_{rs}^* \notag \\ & \overset{(4.11)}{=} \varphi(1) \cdot g(\varphi)(1) \sum_{i,j,r=1}^{^k} g_{ir}c_{ij} (b-\delta)_+ c_{rj}^* \notag \\ & \overset{(4.1)}{=} \varphi(1) \cdot g(\varphi)(1) \sum_{i=1}^{^k} g_{ii} \left( \sum_{j=1}^{k}c_{ij} (b-\delta)_+ c_{ij}^*\right) \notag \\ & \overset{(4.1)}{=} \varphi(1) \cdot g(\varphi)(1) \cdot g(\varphi)(1) \cdot (a-\epsilon)_+ \notag \\ & \overset{(4.2)}{\approx}_{\frac{\mu}{15}} \varphi(1) (a-\epsilon)_+ \notag \\ & \overset{(4.9)}{\approx}_{\frac{2\mu}{15}} a_1. \end{align} $$
On the other hand,
 $$ \begin{align} a_2 & = (a-\varepsilon)_+^{1/2}( f_m(1_{\tilde{A}}-\varphi(1))f_m -\eta)_+ (a-\varepsilon)_+^{1/2} \notag \\ & \overset{(4.3)}{\approx}_{\frac{2\mu}{15}} (a-\varepsilon)_+^{1/2} f_n ( f_m(1_{\tilde{A}}-\varphi(1))f_m -\eta)_+ f_n (a-\eta)_+^{1/2} \notag \\ & \approx_{\eta} (a-\varepsilon)_+^{1/2} f_n f_m(1_{\tilde{A}}-\varphi(1))f_m f_n (a-\varepsilon)_+^{1/2} \notag \\ & = (a-\varepsilon)_+^{1/2} f_n (1_{\tilde{A}}-\varphi(1)) f_n (a-\varepsilon)_+^{1/2} \notag \\ & \approx_{\eta} (a-\varepsilon)_+^{1/2}( f_n(1_{\tilde{A}}-\varphi(1))f_n -\eta)_+ (a-\varepsilon)_+^{1/2}. \end{align} $$
$$ \begin{align} a_2 & = (a-\varepsilon)_+^{1/2}( f_m(1_{\tilde{A}}-\varphi(1))f_m -\eta)_+ (a-\varepsilon)_+^{1/2} \notag \\ & \overset{(4.3)}{\approx}_{\frac{2\mu}{15}} (a-\varepsilon)_+^{1/2} f_n ( f_m(1_{\tilde{A}}-\varphi(1))f_m -\eta)_+ f_n (a-\eta)_+^{1/2} \notag \\ & \approx_{\eta} (a-\varepsilon)_+^{1/2} f_n f_m(1_{\tilde{A}}-\varphi(1))f_m f_n (a-\varepsilon)_+^{1/2} \notag \\ & = (a-\varepsilon)_+^{1/2} f_n (1_{\tilde{A}}-\varphi(1)) f_n (a-\varepsilon)_+^{1/2} \notag \\ & \approx_{\eta} (a-\varepsilon)_+^{1/2}( f_n(1_{\tilde{A}}-\varphi(1))f_n -\eta)_+ (a-\varepsilon)_+^{1/2}. \end{align} $$
Since a is a positive contraction, we obtain
 $$ \begin{align} \left(a_2 - \frac{2\mu}{15} - 2 \eta \right)_+ & \overset{(4.13)}{\precsim} (a-\varepsilon)_+^{1/2}( f_n(1_{\tilde{A}}-\varphi(1))f_n -\eta)_+ (a-\varepsilon)_+^{1/2} \notag \\ & \sim ( f_n(1_{\tilde{A}}-\varphi(1))f_n -\eta)_+^{1/2} (a - \varepsilon)_+ ( f_n(1_{\tilde{A}}-\varphi(1))f_n -\eta)_+^{1/2} \notag \\ & \precsim ( f_n(1_{\tilde{A}}-\varphi(1))f_n -\eta)_+ \notag \\ & \overset{(4.4)}{\precsim} d. \end{align} $$
$$ \begin{align} \left(a_2 - \frac{2\mu}{15} - 2 \eta \right)_+ & \overset{(4.13)}{\precsim} (a-\varepsilon)_+^{1/2}( f_n(1_{\tilde{A}}-\varphi(1))f_n -\eta)_+ (a-\varepsilon)_+^{1/2} \notag \\ & \sim ( f_n(1_{\tilde{A}}-\varphi(1))f_n -\eta)_+^{1/2} (a - \varepsilon)_+ ( f_n(1_{\tilde{A}}-\varphi(1))f_n -\eta)_+^{1/2} \notag \\ & \precsim ( f_n(1_{\tilde{A}}-\varphi(1))f_n -\eta)_+ \notag \\ & \overset{(4.4)}{\precsim} d. \end{align} $$
Thus, there is
![]() $s \in A$
such that
$s \in A$
such that
As before, we can further assume that
![]() $s(b-\delta )_+ =0$
and recall that
$s(b-\delta )_+ =0$
and recall that
![]() $c_{ij}d =0$
. Then
$c_{ij}d =0$
. Then
 $$ \begin{align} (\hat{c} + s)((b-\delta)_+ + d)(\hat{c} + s)^* & = \hat{c}(b-\delta)_+ \hat{c}^* + sds^* \notag \\ & \overset{(4.12)}{\approx}_{\frac{\mu}{3}} a_1 + sds^* \notag \\ & \overset{(4.15)}{\approx}_{\frac{\mu}{5} + 2\eta} a_1 + a_2 \notag \\ & \overset{(4.10)}{\approx}_{\frac{\mu}{3}+ \eta} (a-\epsilon)_+. \end{align} $$
$$ \begin{align} (\hat{c} + s)((b-\delta)_+ + d)(\hat{c} + s)^* & = \hat{c}(b-\delta)_+ \hat{c}^* + sds^* \notag \\ & \overset{(4.12)}{\approx}_{\frac{\mu}{3}} a_1 + sds^* \notag \\ & \overset{(4.15)}{\approx}_{\frac{\mu}{5} + 2\eta} a_1 + a_2 \notag \\ & \overset{(4.10)}{\approx}_{\frac{\mu}{3}+ \eta} (a-\epsilon)_+. \end{align} $$
Since
![]() $\mu $
and
$\mu $
and
![]() $\eta $
are arbitrary small, we get
$\eta $
are arbitrary small, we get
where the last part follows from the construction of
![]() $d=f(b)$
where
$d=f(b)$
where
![]() $\mathrm {supp}f \subseteq [0,\delta /2]$
. Since
$\mathrm {supp}f \subseteq [0,\delta /2]$
. Since
![]() $\epsilon $
is arbitrary, we conclude
$\epsilon $
is arbitrary, we conclude
![]() $a \precsim b$
.
$a \precsim b$
.
We thank the referee for suggesting the following direct proof of the main theorem of this section.
Theorem 4.2 (cf. [Reference Amini, Golestani, Jamali and Phillips1, Theorem 6.4])
Let A be a simple
![]() $\mathrm {C}^*$
-algebra. If A is tracially
$\mathrm {C}^*$
-algebra. If A is tracially
![]() $\mathcal {Z}$
-stable, then
$\mathcal {Z}$
-stable, then
![]() $\mathrm {Cu}(A)$
is almost unperforated (equivalently, A has strict comparison).
$\mathrm {Cu}(A)$
is almost unperforated (equivalently, A has strict comparison).
Proof Let us suppose first that A is
![]() $\sigma $
-unital. By [Reference Castillejos and Evington11, Proposition 2.4], we know that A is either stably isomorphic to a unital
$\sigma $
-unital. By [Reference Castillejos and Evington11, Proposition 2.4], we know that A is either stably isomorphic to a unital
![]() $\mathrm {C}^*$
-algebra or A is stably projectionless. If A is unital, then the result follows from [Reference Hirshberg and Orovitz27, Theorem 3.3], as both tracial
$\mathrm {C}^*$
-algebra or A is stably projectionless. If A is unital, then the result follows from [Reference Hirshberg and Orovitz27, Theorem 3.3], as both tracial
![]() ${\mathcal {Z}}$
-stability and the almost unperforation of the Cuntz semigroup are preserved under stable isomorphism.
${\mathcal {Z}}$
-stability and the almost unperforation of the Cuntz semigroup are preserved under stable isomorphism.
If A is stably projectionless, then it is stably finite. By [Reference Antoine, Perera and Thiel3, Proposition 5.3.16], every nonzero element of
![]() $\mathrm {Cu}(A)$
is either soft or compact. By [Reference Brown and Ciuperca9, Theorem 3.5],
$\mathrm {Cu}(A)$
is either soft or compact. By [Reference Brown and Ciuperca9, Theorem 3.5],
![]() $\langle a \rangle $
is soft if and only if
$\langle a \rangle $
is soft if and only if
![]() $\{0\}$
is an accumulation point of
$\{0\}$
is an accumulation point of
![]() $\sigma (a)$
(see Definition 2.1). Let
$\sigma (a)$
(see Definition 2.1). Let
![]() $\langle a \rangle , \langle b \rangle \in \mathrm {Cu}(A)$
be soft elements such that
$\langle a \rangle , \langle b \rangle \in \mathrm {Cu}(A)$
be soft elements such that
![]() $(k+1)\langle a \rangle \leq k \langle b \rangle $
for some
$(k+1)\langle a \rangle \leq k \langle b \rangle $
for some
![]() $k \in \mathbb {N}$
. It follows that
$k \in \mathbb {N}$
. It follows that
![]() $(k+1)\langle a \rangle \leq (k+1) \langle b \rangle $
and, by Lemma 4.1,
$(k+1)\langle a \rangle \leq (k+1) \langle b \rangle $
and, by Lemma 4.1,
![]() $\langle a \rangle \leq \langle b \rangle $
in
$\langle a \rangle \leq \langle b \rangle $
in
![]() $\mathrm {Cu}(A)$
. Hence, the soft part of
$\mathrm {Cu}(A)$
. Hence, the soft part of
![]() $\mathrm {Cu}(A)$
is almost unperforated. By [Reference Thiel54, Proposition 2.8],
$\mathrm {Cu}(A)$
is almost unperforated. By [Reference Thiel54, Proposition 2.8],
![]() $\mathrm {Cu}(A)$
is almost unperforated as well.
$\mathrm {Cu}(A)$
is almost unperforated as well.
For the general case, let
![]() $a,b \in (A\otimes \mathbb {K})_+$
such that there is some
$a,b \in (A\otimes \mathbb {K})_+$
such that there is some
![]() $k \in \mathbb {N}$
with
$k \in \mathbb {N}$
with
![]() $(k+1) \langle a \rangle _A \leq k \langle b \rangle _A$
in
$(k+1) \langle a \rangle _A \leq k \langle b \rangle _A$
in
![]() $\mathrm {Cu}(A)$
. Let B be a
$\mathrm {Cu}(A)$
. Let B be a
![]() $\sigma $
-unital hereditary subalgebra of A such that
$\sigma $
-unital hereditary subalgebra of A such that
![]() $B\otimes \mathbb {K}$
contains both a and b.Footnote
4
By [Reference Kirchberg and Rørdam33, Lemma 2.2],
$B\otimes \mathbb {K}$
contains both a and b.Footnote
4
By [Reference Kirchberg and Rørdam33, Lemma 2.2],
![]() $(k+1)\langle a \rangle _B \leq k \langle b \rangle _B$
in
$(k+1)\langle a \rangle _B \leq k \langle b \rangle _B$
in
![]() $\mathrm {Cu}(B)$
. By Proposition 3.6, B is tracially
$\mathrm {Cu}(B)$
. By Proposition 3.6, B is tracially
![]() ${\mathcal {Z}}$
-stable and hence, by the first part of this proof,
${\mathcal {Z}}$
-stable and hence, by the first part of this proof,
![]() $\mathrm {Cu}(B)$
is almost unperforated. It follows that
$\mathrm {Cu}(B)$
is almost unperforated. It follows that
![]() $\langle a \rangle _B \leq \langle b \rangle _B$
in
$\langle a \rangle _B \leq \langle b \rangle _B$
in
![]() $\mathrm {Cu}(B)$
, which clearly yields
$\mathrm {Cu}(B)$
, which clearly yields
![]() $\langle a \rangle _A \leq \langle b \rangle _A$
. This shows that
$\langle a \rangle _A \leq \langle b \rangle _A$
. This shows that
![]() $\mathrm {Cu}(A)$
is almost unperforated.
$\mathrm {Cu}(A)$
is almost unperforated.
5
 ${\mathcal {Z}}$
-stability
${\mathcal {Z}}$
-stability
This is the main section of this note. We aim to show that tracial
![]() ${\mathcal {Z}}$
-stability is equivalent to
${\mathcal {Z}}$
-stability is equivalent to
![]() ${\mathcal {Z}}$
-stability in the separable simple nuclear setting. We begin with the easy part.
${\mathcal {Z}}$
-stability in the separable simple nuclear setting. We begin with the easy part.
Proposition 5.1 Let A be a simple
![]() ${\mathcal {Z}}$
-stable
${\mathcal {Z}}$
-stable
![]() $\mathrm {C}^*$
-algebra. Then A is tracially
$\mathrm {C}^*$
-algebra. Then A is tracially
![]() ${\mathcal {Z}}$
-stable.
${\mathcal {Z}}$
-stable.
Proof By assumption, we have
![]() $A\cong A\otimes {\mathcal {Z}}$
, so by Proposition 3.7, it suffices to know that
$A\cong A\otimes {\mathcal {Z}}$
, so by Proposition 3.7, it suffices to know that
![]() ${\mathcal {Z}}$
is itself tracially
${\mathcal {Z}}$
is itself tracially
![]() ${\mathcal {Z}}$
-stable. But this is well known (see, for example, [Reference Hirshberg and Orovitz27, Proposition 2.2]).
${\mathcal {Z}}$
-stable. But this is well known (see, for example, [Reference Hirshberg and Orovitz27, Proposition 2.2]).
The notion of property (SI), introduced by Matui and Sato in [Reference Matui and Sato40], has been fundamental in many recent developments in the structure and classification of simple nuclear
![]() $\mathrm {C}^*$
-algebras. It was originally introduced for simple unital
$\mathrm {C}^*$
-algebras. It was originally introduced for simple unital
![]() $\mathrm {C}^*$
-algebras in [Reference Matui and Sato40, Definition 4.1] and has been recently revised by the third-named author in [Reference Szabó53], in which a general framework was developed to cover the class of all simple separable nuclear
$\mathrm {C}^*$
-algebras in [Reference Matui and Sato40, Definition 4.1] and has been recently revised by the third-named author in [Reference Szabó53], in which a general framework was developed to cover the class of all simple separable nuclear
![]() $\mathrm {C}^*$
-algebras. Let us record some of the ingredients needed in this note.
$\mathrm {C}^*$
-algebras. Let us record some of the ingredients needed in this note.
Definition 5.2 ([Reference Szabó53, Definition 2.5])
Let A be a separable simple
![]() $\mathrm {C}^*$
-algebra.
$\mathrm {C}^*$
-algebra.
-
(i) A positive contraction
 $f \in F_{\omega }(A)$
is called tracially supported at 1, if one of the following is true: A is traceless, and
$f \in F_{\omega }(A)$
is called tracially supported at 1, if one of the following is true: A is traceless, and
 $\|fa\|= \|a\|$
for all
$\|fa\|= \|a\|$
for all
 $a \in A_+$
; or
$a \in A_+$
; or
 $T^+(A)\neq \{0,\infty \}$
, and for all nonzero positive
$T^+(A)\neq \{0,\infty \}$
, and for all nonzero positive
 $a \in \mathrm {Ped}(A)$
, there exists a constant
$a \in \mathrm {Ped}(A)$
, there exists a constant
 $\kappa _{f,a}>0$
such that for all
$\kappa _{f,a}>0$
such that for all $$ \begin{align*} \inf_{m \geq 1} \tau_a (f^m) \geq \kappa_{f,a} \tau(a) \end{align*} $$
$$ \begin{align*} \inf_{m \geq 1} \tau_a (f^m) \geq \kappa_{f,a} \tau(a) \end{align*} $$
 $\tau \in T_{\omega }^+ (A)$
with
$\tau \in T_{\omega }^+ (A)$
with
 $\tau |_A$
nontrivial.
$\tau |_A$
nontrivial.
-
(ii) A positive element
 $e \in F_{\omega }(A)$
is called tracially null if
$e \in F_{\omega }(A)$
is called tracially null if
 $\tau _a(e) = 0$
for all nonzero positive
$\tau _a(e) = 0$
for all nonzero positive
 $a \in \mathrm {Ped}(A)$
and
$a \in \mathrm {Ped}(A)$
and
 $\tau \in T_{\omega }^+(A)$
with
$\tau \in T_{\omega }^+(A)$
with
 $\tau (a) < \infty $
.
$\tau (a) < \infty $
.
Either one of the conditions above holds for all nonzero positive
![]() $a\in \mathrm {Ped}(A)$
if it holds for just one such element.
$a\in \mathrm {Ped}(A)$
if it holds for just one such element.
Definition 5.3 ([Reference Szabó53, Definition 2.7])
Let A be a separable simple
![]() $\mathrm {C}^*$
-algebra. It is said that A has property (SI) if whenever
$\mathrm {C}^*$
-algebra. It is said that A has property (SI) if whenever
![]() $e,f \in F_{\omega }(A)$
are positive contractions with f tracially supported at 1 and e tracially null, there exists a contraction
$e,f \in F_{\omega }(A)$
are positive contractions with f tracially supported at 1 and e tracially null, there exists a contraction
![]() $s\in F_{\omega }(A)$
with
$s\in F_{\omega }(A)$
with
Importantly, it follows from [Reference Szabó53, Corollary 3.10] that nonelementary separable simple nuclear
![]() $\mathrm {C}^*$
-algebras with strict comparison have property (SI). For completeness, we include a proof of the following folklore result, which is well known to the experts. The underlying argument has appeared in the literature several times before.
$\mathrm {C}^*$
-algebras with strict comparison have property (SI). For completeness, we include a proof of the following folklore result, which is well known to the experts. The underlying argument has appeared in the literature several times before.
Proposition 5.4 (Matui–Sato)
Let A be a simple, separable, and nuclear
![]() $\mathrm {C}^*$
-algebra with strict comparison and
$\mathrm {C}^*$
-algebra with strict comparison and
![]() $T^+(A) \neq \{0,\infty \}$
. Then A is uniformly McDuff if and only if A is
$T^+(A) \neq \{0,\infty \}$
. Then A is uniformly McDuff if and only if A is
![]() ${\mathcal {Z}}$
-stable.
${\mathcal {Z}}$
-stable.
Proof The “if” part is clear by Remark 2.6, so we proceed to prove the “only if” part.
It follows from [Reference Szabó53, Corollary 3.10] that A has property (SI). For each
![]() $n \in \mathbb {N}$
, there is a tracially large order zero map
$n \in \mathbb {N}$
, there is a tracially large order zero map
![]() $\varphi : M_n(\mathbb {C}) \to F_{\omega }(A)$
. Set
$\varphi : M_n(\mathbb {C}) \to F_{\omega }(A)$
. Set
![]() $e:= 1_{F_{\omega }(A)} - \varphi (1)\in F_{\omega }(A)$
and
$e:= 1_{F_{\omega }(A)} - \varphi (1)\in F_{\omega }(A)$
and
![]() $f:=\varphi (e_{11})\in F_{\omega }(A)$
. The fact that
$f:=\varphi (e_{11})\in F_{\omega }(A)$
. The fact that
![]() $\varphi $
is tracially large means precisely that e is tracially null. Let us check that f is tracially supported at 1.
$\varphi $
is tracially large means precisely that e is tracially null. Let us check that f is tracially supported at 1.
Since the tracially null elements form an ideal and
![]() $\varphi (1)$
agrees with the unit of
$\varphi (1)$
agrees with the unit of
![]() $F_{\omega }(A)$
modulo this ideal, we also get that
$F_{\omega }(A)$
modulo this ideal, we also get that
![]() $1_{F_{\omega }(A)}-\varphi (1)^m$
is tracially null for any
$1_{F_{\omega }(A)}-\varphi (1)^m$
is tracially null for any
![]() $m\geq 1$
. This shows that
$m\geq 1$
. This shows that
![]() $\left (1_{F_{\omega }(A)}-\varphi (1)^m\right )f$
is tracially null and
$\left (1_{F_{\omega }(A)}-\varphi (1)^m\right )f$
is tracially null and
Recall that by the structure theorem of order zero maps, we have
![]() $\varphi (e_{11})^m = \varphi (1)^{m-1} \varphi (e_{11})$
(see Section 2.2). Thus,
$\varphi (e_{11})^m = \varphi (1)^{m-1} \varphi (e_{11})$
(see Section 2.2). Thus,
for all nonzero positive
![]() $a \in \mathrm {Ped}(A)$
and
$a \in \mathrm {Ped}(A)$
and
![]() $\tau \in T^+_{\omega }(A)$
with
$\tau \in T^+_{\omega }(A)$
with
![]() $\tau (a) < \infty $
. Observe that, by uniqueness of the tracial state
$\tau (a) < \infty $
. Observe that, by uniqueness of the tracial state
![]() $\mathrm {tr}$
on
$\mathrm {tr}$
on
![]() $M_n(\mathbb C)$
,
$M_n(\mathbb C)$
,
![]() $\tau _a\circ \varphi $
must be a multiple of
$\tau _a\circ \varphi $
must be a multiple of
![]() $\mathrm {tr}$
. Then
$\mathrm {tr}$
. Then
for all nonzero positive
![]() $a \in \mathrm {Ped}(A)$
and
$a \in \mathrm {Ped}(A)$
and
![]() $\tau \in T^+_{\omega }(A)$
with
$\tau \in T^+_{\omega }(A)$
with
![]() $\tau (a) < \infty $
. It follows that f is tracially supported at
$\tau (a) < \infty $
. It follows that f is tracially supported at
![]() $1$
.
$1$
.
By property (SI), there exists
![]() $s \in F_{\omega }(A)$
such that
$s \in F_{\omega }(A)$
such that
![]() $fs=s$
and
$fs=s$
and
![]() $s^*s = e$
. By [Reference Rørdam and Winter51, Proposition 5.1(iii)], there is a unital
$s^*s = e$
. By [Reference Rørdam and Winter51, Proposition 5.1(iii)], there is a unital
![]() $^*$
-homomorphism from the dimension drop algebraFootnote
5
$^*$
-homomorphism from the dimension drop algebraFootnote
5
![]() $Z_{n,n+1}$
into
$Z_{n,n+1}$
into
![]() $F_{\omega }(A)$
for all
$F_{\omega }(A)$
for all
![]() $n \in \mathbb {N}$
. By [Reference Nawata42, Proposition 5.1], we conclude that A is
$n \in \mathbb {N}$
. By [Reference Nawata42, Proposition 5.1], we conclude that A is
![]() ${\mathcal {Z}}$
-stable.
${\mathcal {Z}}$
-stable.
Next, we will show that tracial
![]() ${\mathcal {Z}}$
-stability implies the uniform McDuff property. Let us prove a preliminary lemma first.
${\mathcal {Z}}$
-stability implies the uniform McDuff property. Let us prove a preliminary lemma first.
Lemma 5.5 (cf. [Reference Hirshberg and Orovitz27, Lemma 4.3])
Let A be a simple nonelementary
![]() $\mathrm {C}^*$
-algebra with
$\mathrm {C}^*$
-algebra with
![]() $T^+(A)\neq \{0,\infty \}$
. Suppose that
$T^+(A)\neq \{0,\infty \}$
. Suppose that
![]() $K\subset T^+(A)\setminus \{0,\infty \}$
is a compact subset. Then, for any
$K\subset T^+(A)\setminus \{0,\infty \}$
is a compact subset. Then, for any
![]() $n \in \mathbb {N}$
, there exists a positive element
$n \in \mathbb {N}$
, there exists a positive element
![]() $c_n\in A$
of norm one such that
$c_n\in A$
of norm one such that
![]() $d_{\tau }(c_n) \leq \frac {1}{n}$
for all
$d_{\tau }(c_n) \leq \frac {1}{n}$
for all
![]() $\tau \in K$
.
$\tau \in K$
.
Proof Let b be a nonzero positive element in
![]() $\mathrm {Ped}(A)$
. Then, by compactness, we have
$\mathrm {Ped}(A)$
. Then, by compactness, we have
![]() $\sup _{\sigma \in K} d_{\sigma }(b)<\infty $
, so let us choose a natural number
$\sup _{\sigma \in K} d_{\sigma }(b)<\infty $
, so let us choose a natural number
![]() $k\in \mathbb {N}$
greater than this constant. In particular, each trace
$k\in \mathbb {N}$
greater than this constant. In particular, each trace
![]() $\tau \in K$
restricts to a positive tracial functional of norm at most k on the hereditary subalgebra
$\tau \in K$
restricts to a positive tracial functional of norm at most k on the hereditary subalgebra
![]() $\overline {bAb}$
. Using [Reference Kirchberg and Rørdam33, Proposition 4.10] and [Reference Winter and Zacharias62, Corollary 4.1], there exists a c.p.c. order zero map
$\overline {bAb}$
. Using [Reference Kirchberg and Rørdam33, Proposition 4.10] and [Reference Winter and Zacharias62, Corollary 4.1], there exists a c.p.c. order zero map
![]() $\psi : M_{nk}(\mathbb {C}) \to \overline {bAb}$
such that
$\psi : M_{nk}(\mathbb {C}) \to \overline {bAb}$
such that
![]() $c_n:= \psi (e_{11})$
is a positive contraction of norm one in A. Given
$c_n:= \psi (e_{11})$
is a positive contraction of norm one in A. Given
![]() $\tau \in K$
, it follows that
$\tau \in K$
, it follows that
 $$ \begin{align} nk\cdot d_{\tau}(\psi(e_{11}))=d_{\tau}\left(\sum_{i=1}^{nk}\psi(e_{ii})\right) = d_{\tau}(b)\leq k. \end{align} $$
$$ \begin{align} nk\cdot d_{\tau}(\psi(e_{11}))=d_{\tau}\left(\sum_{i=1}^{nk}\psi(e_{ii})\right) = d_{\tau}(b)\leq k. \end{align} $$
Therefore
![]() $c_n$
satisfies the required property.
$c_n$
satisfies the required property.
Proposition 5.6 Let A be a separable simple
![]() $\mathrm {C}^*$
-algebra with
$\mathrm {C}^*$
-algebra with
![]() $T^+(A) \neq \{0,\infty \}$
. If A is tracially
$T^+(A) \neq \{0,\infty \}$
. If A is tracially
![]() ${\mathcal {Z}}$
-stable, then A is uniformly McDuff.
${\mathcal {Z}}$
-stable, then A is uniformly McDuff.
Proof Pick any nonzero positive element
![]() $b\in \mathrm {Ped}(A)$
, and define the subset
$b\in \mathrm {Ped}(A)$
, and define the subset
![]() $K\subset T^+(A)\setminus \{0,\infty \}$
as those traces that normalize b. Then K is clearly compact and every nontrivial trace on A is a constant multiple of a trace in K. Let
$K\subset T^+(A)\setminus \{0,\infty \}$
as those traces that normalize b. Then K is clearly compact and every nontrivial trace on A is a constant multiple of a trace in K. Let
![]() $c_k \in A$
be the positive elements of norm one given from Lemma 5.5 for
$c_k \in A$
be the positive elements of norm one given from Lemma 5.5 for
![]() $k \in \mathbb {N}$
, and let
$k \in \mathbb {N}$
, and let
![]() $c \in B_{\omega }$
be the induced element. We claim that
$c \in B_{\omega }$
be the induced element. We claim that
![]() $\tau (c) = 0$
for any
$\tau (c) = 0$
for any
![]() $\tau \in T^+_{\omega }(A)$
with
$\tau \in T^+_{\omega }(A)$
with
![]() $\tau (b)<\infty $
. Indeed, clearly,
$\tau (b)<\infty $
. Indeed, clearly,
![]() $\tau (c)=0$
whenever
$\tau (c)=0$
whenever
![]() $\tau $
is induced from a sequence
$\tau $
is induced from a sequence
![]() $\tau _n\in K$
. However, if
$\tau _n\in K$
. However, if
![]() $\tau (b)<\infty $
, then by [Reference Szabó53, Lemma 2.10 and Remark 2.11],
$\tau (b)<\infty $
, then by [Reference Szabó53, Lemma 2.10 and Remark 2.11],
![]() $\tau $
is already a constant multiple of some generalized limit trace induced from a sequence in K, so the claim follows.
$\tau $
is already a constant multiple of some generalized limit trace induced from a sequence in K, so the claim follows.
Let
![]() $n\in \mathbb {N}$
. By Proposition 3.5, there are a c.p.c. order zero map
$n\in \mathbb {N}$
. By Proposition 3.5, there are a c.p.c. order zero map
![]() $\varphi : M_n(\mathbb {C}) \to A_{\omega } \cap A'$
and a contraction
$\varphi : M_n(\mathbb {C}) \to A_{\omega } \cap A'$
and a contraction
![]() $x\in A_{\omega }$
such that
$x\in A_{\omega }$
such that
Let us show that this map induces a tracially large map into
![]() $F_{\omega }(A)$
. Indeed, we have for any
$F_{\omega }(A)$
. Indeed, we have for any
![]() $\tau \in T^+_{\omega }(A)$
with
$\tau \in T^+_{\omega }(A)$
with
![]() $\tau (b)<\infty $
that
$\tau (b)<\infty $
that
 $$\begin{align*}\begin{array}{ccl} \tau(b^{1/2}(1_{\tilde A_{\omega}} - \varphi(1_{M_n}))b^{1/2}) &\overset{(5.6)}{=}& \tau( b^{1/2} x^* c x b^{1/2}) \\ &=& \tau(c^{1/2}xbx^*c^{1/2}) \\ & \leq & \|x\|^2\|b\|\tau(c) = 0. \end{array} \end{align*}$$
$$\begin{align*}\begin{array}{ccl} \tau(b^{1/2}(1_{\tilde A_{\omega}} - \varphi(1_{M_n}))b^{1/2}) &\overset{(5.6)}{=}& \tau( b^{1/2} x^* c x b^{1/2}) \\ &=& \tau(c^{1/2}xbx^*c^{1/2}) \\ & \leq & \|x\|^2\|b\|\tau(c) = 0. \end{array} \end{align*}$$
This shows that
![]() $1-\varphi (1_{M_n})$
vanishes under the trace
$1-\varphi (1_{M_n})$
vanishes under the trace
![]() $\tau _b$
. As explained in the footnote at Definition 2.4, [Reference Szabó53, Proposition 2.4] yields that
$\tau _b$
. As explained in the footnote at Definition 2.4, [Reference Szabó53, Proposition 2.4] yields that
![]() $1-\varphi (1_{M_n})$
vanishes under any trace
$1-\varphi (1_{M_n})$
vanishes under any trace
![]() $\tau _a$
with
$\tau _a$
with
![]() $a\in \mathrm {Ped}(A)$
and
$a\in \mathrm {Ped}(A)$
and
![]() $\tau \in T^+_{\omega }(A)$
satisfying
$\tau \in T^+_{\omega }(A)$
satisfying
![]() $\tau (a) < \infty $
. Hence, the induced map
$\tau (a) < \infty $
. Hence, the induced map
![]() $\bar \varphi : M_n(\mathbb {C}) \to F_{\omega }(A)$
is tracially large and A is uniformly McDuff.
$\bar \varphi : M_n(\mathbb {C}) \to F_{\omega }(A)$
is tracially large and A is uniformly McDuff.
Theorem 5.7 Let A be a separable simple nuclear
![]() $\mathrm {C}^*$
-algebra. If A is tracially
$\mathrm {C}^*$
-algebra. If A is tracially
![]() ${\mathcal {Z}}$
-stable, then A is
${\mathcal {Z}}$
-stable, then A is
![]() ${\mathcal {Z}}$
-stable.
${\mathcal {Z}}$
-stable.
Proof By [Reference Castillejos and Evington11, Proposition 2.4], we know that A is either stably projectionless or A is stably isomorphic to a unital
![]() $\mathrm {C}^*$
-algebra. If A is stably isomorphic to a unital
$\mathrm {C}^*$
-algebra. If A is stably isomorphic to a unital
![]() $\mathrm {C}^*$
-algebra, say B, it follows by Corollary 3.8 that B is tracially
$\mathrm {C}^*$
-algebra, say B, it follows by Corollary 3.8 that B is tracially
![]() ${\mathcal {Z}}$
-stable. By [Reference Hirshberg and Orovitz27, Theorem 4.1], it follows that B is
${\mathcal {Z}}$
-stable. By [Reference Hirshberg and Orovitz27, Theorem 4.1], it follows that B is
![]() ${\mathcal {Z}}$
-stable. Since
${\mathcal {Z}}$
-stable. Since
![]() ${\mathcal {Z}}$
-stability is preserved under stable isomorphism, it follows that A is
${\mathcal {Z}}$
-stability is preserved under stable isomorphism, it follows that A is
![]() ${\mathcal {Z}}$
-stable. On the other hand, if A is stably projectionless, then A is stably finite. Recall that A has strict comparison by Theorem 4.2. Thus, Propositions 5.4 and 5.6 yield that A is
${\mathcal {Z}}$
-stable. On the other hand, if A is stably projectionless, then A is stably finite. Recall that A has strict comparison by Theorem 4.2. Thus, Propositions 5.4 and 5.6 yield that A is
![]() ${\mathcal {Z}}$
-stable.
${\mathcal {Z}}$
-stable.
Matui introduced the notion of almost finiteness for étale groupoids with a compact and totally disconnected unit space (see [Reference Matui39, Definition 6.2] and we also refer the reader to [Reference Renault47] for the theory of étale groupoids). Recently, the notion of strongly almost finiteness was introduced in [Reference Ara, Bönicke, Bosa and Li5, Definition 3.12] for étale groupoids G with a (not necessarily compact) totally disconnected unit space. More precisely, G is strongly almost finite if the restriction
![]() $G|_K$
is almost finite in the sense of Matui for all compact open subsets K of the unit space
$G|_K$
is almost finite in the sense of Matui for all compact open subsets K of the unit space
![]() $G^{(0)}$
. So the reduced groupoid
$G^{(0)}$
. So the reduced groupoid
![]() $\mathrm {C}^*$
-algebra
$\mathrm {C}^*$
-algebra
![]() $C_r^*(G)$
may not be unital in general. Moreover, it is known that when the groupoid is also minimal and has a compact unit space, strong almost finiteness agrees with Matui’s almost finiteness (see [Reference Ara, Bönicke, Bosa and Li5, Proposition 3.6]). It is also worth noting that (strong) almost finiteness does not imply amenability for groupoids nor exactness for groupoid
$C_r^*(G)$
may not be unital in general. Moreover, it is known that when the groupoid is also minimal and has a compact unit space, strong almost finiteness agrees with Matui’s almost finiteness (see [Reference Ara, Bönicke, Bosa and Li5, Proposition 3.6]). It is also worth noting that (strong) almost finiteness does not imply amenability for groupoids nor exactness for groupoid
![]() $\mathrm {C}^*$
-algebras (see [Reference Elek15, Theorem 6] and [Reference Ara, Bönicke, Bosa and Li4, Remark 2.10]).
$\mathrm {C}^*$
-algebras (see [Reference Elek15, Theorem 6] and [Reference Ara, Bönicke, Bosa and Li4, Remark 2.10]).
Corollary 5.8 Let G be a locally compact Hausdorff minimal
![]() $\sigma $
-compact étale groupoid with totally disconnected unit space
$\sigma $
-compact étale groupoid with totally disconnected unit space
![]() $G^{(0)}$
without isolated points. If G is strongly almost finite, then the reduced
$G^{(0)}$
without isolated points. If G is strongly almost finite, then the reduced
![]() $\mathrm {C}^*$
-algebra
$\mathrm {C}^*$
-algebra
![]() $C_r^*(G)$
is a
$C_r^*(G)$
is a
![]() $\sigma $
-unital simple and tracially
$\sigma $
-unital simple and tracially
![]() ${\mathcal {Z}}$
-stable
${\mathcal {Z}}$
-stable
![]() $\mathrm {C}^*$
-algebra with real rank zero and stable rank one.
$\mathrm {C}^*$
-algebra with real rank zero and stable rank one.
If G is also amenable and second-countable, then
![]() $C_r^*(G)$
is classifiable by its Elliott invariant and has decomposition rank at most one.
$C_r^*(G)$
is classifiable by its Elliott invariant and has decomposition rank at most one.
Proof Fix a compact open subset
![]() $K\subseteq G^{(0)}$
. Since G is minimal, it follows that G and the restriction
$K\subseteq G^{(0)}$
. Since G is minimal, it follows that G and the restriction
![]() $G|_K$
are Morita-equivalent. Hence,
$G|_K$
are Morita-equivalent. Hence,
![]() $C_r^*(G)$
and
$C_r^*(G)$
and
![]() $C_r^*(G|_K)$
are stably isomorphic by [Reference Carlsen, Ruiz and Sims10, Theorem 2.1]. On the other hand,
$C_r^*(G|_K)$
are stably isomorphic by [Reference Carlsen, Ruiz and Sims10, Theorem 2.1]. On the other hand,
![]() $G|_K$
is a minimal, almost finite,
$G|_K$
is a minimal, almost finite,
![]() $\sigma $
-compact étale groupoid with compact totally disconnected unit space K. As K is clopen in
$\sigma $
-compact étale groupoid with compact totally disconnected unit space K. As K is clopen in
![]() $G^{(0)}$
, K has no isolated points as well. By [Reference Ma and Wu38, Corollary 9.11], we deduce that
$G^{(0)}$
, K has no isolated points as well. By [Reference Ma and Wu38, Corollary 9.11], we deduce that
![]() $C_r^*(G|_K)$
is a unital simple and tracially
$C_r^*(G|_K)$
is a unital simple and tracially
![]() ${\mathcal {Z}}$
-stable
${\mathcal {Z}}$
-stable
![]() $\mathrm {C}^*$
-algebra. Moreover,
$\mathrm {C}^*$
-algebra. Moreover,
![]() $C_r^*(G|_K)$
has real rank zero and stable rank one (see [Reference Ara, Bönicke, Bosa and Li4, Reference Suzuki52]). Hence, we conclude that
$C_r^*(G|_K)$
has real rank zero and stable rank one (see [Reference Ara, Bönicke, Bosa and Li4, Reference Suzuki52]). Hence, we conclude that
![]() $C_r^*(G)$
satisfies the desired properties by Corollary 3.8.
$C_r^*(G)$
satisfies the desired properties by Corollary 3.8.
If we also assume amenability and second-countability for G, then
![]() $C_r^*(G)$
is also a nuclear separable
$C_r^*(G)$
is also a nuclear separable
![]() ${\mathcal {Z}}$
-stable
${\mathcal {Z}}$
-stable
![]() $\mathrm {C}^*$
-algebra in the UCT class by Theorem 5.7 and [Reference Tu58]. Notice that by [Reference Suzuki52, Lemma 3.9], we have
$\mathrm {C}^*$
-algebra in the UCT class by Theorem 5.7 and [Reference Tu58]. Notice that by [Reference Suzuki52, Lemma 3.9], we have
![]() $T^+(C_r^*(G))\neq \{0,\infty \}$
. Finally, [Reference Castillejos and Evington11, Theorem 7.2 and Remark 7.3] together imply that
$T^+(C_r^*(G))\neq \{0,\infty \}$
. Finally, [Reference Castillejos and Evington11, Theorem 7.2 and Remark 7.3] together imply that
![]() $C_r^*(G)$
has decomposition rank at most one as desired.
$C_r^*(G)$
has decomposition rank at most one as desired.
Acknowledgment
We would like to thank the anonymous referee for useful suggestions on an earlier version of this paper.