Hostname: page-component-54dcc4c588-smtgx Total loading time: 0 Render date: 2025-09-15T05:56:02.172Z Has data issue: false hasContentIssue false
  • English
  • Français

On Whitney-type Characterization of Approximate Differentiability on Metric Measure Spaces

Published online by Cambridge University Press:  20 November 2018

E. Durand-Cartagena ,
L. Ihnatsyeva ,
R. Korte  and
M. Szumańska
E. Durand-Cartagena
Affiliation:
Departamento de Matemática Aplicada, ETSI Industriales, UNED c/Juan del Rosal 12 Ciudad Universitaria, 28040 Madrid, Spain. e-mail: edurand@ind.uned.es
L. Ihnatsyeva
Affiliation:
Department of Mathematics and Statistics, P.O. Box 68, FI-00014 University of Helsinki, Finland. e-mail: lizaveta.ihnatsyeva@helsinki.fi, riikka.korte@helsinki.fi
R. Korte
Affiliation:
Department of Mathematics and Statistics, P.O. Box 68, FI-00014 University of Helsinki, Finland. e-mail: lizaveta.ihnatsyeva@helsinki.fi, riikka.korte@helsinki.fi
M. Szumańska
Affiliation:
Faculty of Mathematics, Informatics, and Mechanics University of Warsaw, Banacha 2, 02-097 Warszawa, Poland. e-mail: m.szumanska@mimuw.edu.pl
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We study approximately differentiable functions on metric measure spaces admitting a Cheeger differentiable structure. The main result is a Whitney-type characterization of approximately differentiable functions in this setting. As an application, we prove a Stepanov-type theorem and consider approximate differentiability of Sobolev, 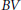$BV$ , and maximal functions.

Keywords

26B0528A1528A7546E35approximate differentiabilitymetric spacestrong measurable differentiable structure,Whitney theorem

Information

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 66 , Issue 4 , 01 August 2014 , pp. 721 - 742
Copyright
Copyright © Canadian Mathematical Society 2014

Footnotes

The first author was partially supported by grant MTM2009-07848 (Spain). The second, the third andthe fourth authors were supported by the Academy of Finland (grants 252293, 250403 and 138738). Thefourth author was partially supported by MNiSW Grant no N N201 397737, Nonlinear partial differentialequations: geometric and variational problems.

References

[1] Aalto, D. and Kinnunen, J., The discrete maximal operator in metric spaces. J. Anal. Math. 111(2010), 369–390. http://dx.doi.org/10.1007/s11854-010-0022-3 CrossRefGoogle Scholar
[2] Aalto, D., Maximal functions in Sobolev spaces. In: Sobolev spaces in mathematics. I, Int. Math. Ser. (N. Y.), 8, Springer, New York, 2009, pp. 25–67.Google Scholar
[3] Ambrosio, L. and Tilli, P., Topics on analysis in metric spaces. Oxford Lecture Series in Mathematics and its Applications, 25, Oxford University Press, Oxford, 2004.Google Scholar
[4] Balogh, Z. M., Rogovin, K., and Zürcher, T., The Stepanov differentiability theorem in metric measure spaces. J. Geom. Anal. 14(2004), no. 3, 405–422. http://dx.doi.org/10.1007/BF02922098 CrossRefGoogle Scholar
[5] Basalaev, S. G.and Vodopyanov, S. K., Approximate differentiability of mappings of Carnot-Carathéodory spaces. 2012. http://arxiv:1206.5197 Google Scholar
[6] Bate, D. and Speight, G., Differentiability, porosity and doubling in metric measure spaces. Proc. Amer. Math. Soc. 141(2013), no. 3, 971–985. http://dx.doi.org/10.1090/S0002-9939-2012-11457-1 CrossRefGoogle Scholar
[7] Björn, A. and Björn, J., Nonlinear potential theory on metric spaces. EMS Tracts in Mathematics, 17, European Mathematical Society, Zürich, 2011.Google Scholar
[8] Björn, A., Björn, J., and Shanmugalingam, N., The Dirichlet problem for p-harmonic functions on metric spaces. J. Reine Angew. Math. 556(2003), 173–203.Google Scholar
[9] Björn, J., Lq-differentials for weighted Sobolev spaces. Michigan Math. J. 47(2000), no. 1, 151–161. http://dx.doi.org/10.1307/mmj/1030374674 CrossRefGoogle Scholar
[10] Bojarski, B., Differentiation of measurable functions and Whitney-Luzin type structure theorems. Helsinki University of Technology Institute of Mathematics Research Reports, 2009.Google Scholar
[11] Buckley, S. M., Is the maximal function of a Lipschitz function continuous? Ann. Acad. Sci. Fenn. Math. 24(1999), no. 2, 519–528.Google Scholar
[12] Cheeger, J., Differentiability of Lipschitz Functions on metric measure spaces. Geom. Funct. Anal. 9(1999), no. 3, 428–517. http://dx.doi.org/10.1007/s000390050094 CrossRefGoogle Scholar
[13] Denjoy, A., Sur les fonctions dérivées sommables. Bull. Soc. Math. France 43(1915), 161–248.CrossRefGoogle Scholar
[14] Durand-Cartagena, E., Jaramillo, J. A., andShanmugalingam, N., The∞-Poincaréinequality in metric measure spaces. Michigan Math. J. 61(2012), no. 1, 63–85. http://dx.doi.org/10.1307/mmj/1331222847 CrossRefGoogle Scholar
[15] Evans, L. C. and Gariepy, R. F., Measure theory and fine properties of functions. Studies in Advanced Mathematics, CRC Press, Boca Raton, FL, 1992.Google Scholar
[16] Federer, H., Geometric measure theory. Die Grundlehren der mathematischenWissenschaften, 153, Springer-Verlag New York Inc., New York, 1969.Google Scholar
[17] Hajłasz, P., Sobolev spaces on metric-measure spaces. In: Heat kernels and analysis on manifolds, graphs, and metric spaces (Paris, 2002), Contemp. Math., 338, Amer. Math. Soc., Providence, RI, 2003, pp. 173–218.Google Scholar
[18] Hajłasz, P. and Koskela, P., Sobolev met Poincaré. Mem. Amer. Math. Soc. 145(2000), no. 688.Google Scholar
[19] Hajłasz, P. and J. Malý, , On approximate differentiability of the maximal function. Proc. Amer. Math. Soc. 138(2010), no. 1, 165–174. http://dx.doi.org/10.1090/S0002-9939-09-09971-7 CrossRefGoogle Scholar
[20] Heinonen, J. and Koskela, P., Quasiconformal maps in metric spaces with controlled geometry. Acta Math. 181(1998), no. 1, 1–61. http://dx.doi.org/10.1007/BF02392747 CrossRefGoogle Scholar
[21] Heinonen, J., Lectures on analysis on metric spaces. Universitext, Springer-Verlag, New York, 2001.Google Scholar
[22] Heinonen, J., Nonsmooth calculus. Bull. Amer. Math. Soc. (N.S.) 44(2007), no. 2, 163–232. http://dx.doi.org/10.1090/S0273-0979-07-01140-8 CrossRefGoogle Scholar
[23] Keith, S., A differentiable structure for metric measure spaces. Adv. Math. 183(2004), no. 2, 271–315. http://dx.doi.org/10.1016/S0001-8708(03)00089-6 CrossRefGoogle Scholar
[24] Keith, S., Measurable differentiable structures and the Poincaré inequality. Indiana Univ. Math. J. 53(2004), no. 4, 1127–1150. http://dx.doi.org/10.1512/iumj.2004.53.2417 CrossRefGoogle Scholar
[25] Kinnunen, J., The Hardy-Littlewood operator of a Sobolev function. Israel J. Math. 100(1997), 117–124. http://dx.doi.org/10.1007/BF02773636 CrossRefGoogle Scholar
[26] Kinnunen, J. and Latvala, V., Lebesgue points for Sobolev functions on metric spaces. Rev. Mat. Iberoamericana 18(2002), no. 3, 685–700. http://dx.doi.org/10.4171/RMI/332 CrossRefGoogle Scholar
[27] Kleiner, B.and Mackay, J., Differentiable structures on metric measure spaces: A Primer. 2011. http://arxiv:1108.1324.Google Scholar
[28] Lahti, P. and Tuominen, H., A pointwise characterization of functions of bounded variation on metric spaces. 2012. http://arxiv:1301.6897 Google Scholar
[29] Liu, F. C., Luzin type property of Sobolev functions. Indiana Univ. Math. J. 26(1977), no. 4, 645–651. http://dx.doi.org/10.1512/iumj.1977.26.26051 CrossRefGoogle Scholar
[30] Liu, F. C. and Tai, W. S., Approximate Taylor polynomials and differentiation of functions. Topol. Methods Nonlinear Anal. 3(1994), no. 1, 189–196.CrossRefGoogle Scholar
[31] Liu, F. C., Lusin properties and interpolation of Sobolev spaces. Topol. Methods Nonlinear Anal. 9(1997), no. 1, 163–177.10.12775/TMNA.1997.007CrossRefGoogle Scholar
[32] H. Luiro, On the size of the set of non-differentiability points of maximal function.2012. arxiv:1208.3971Google Scholar
[33] Luzin, N., Sur les proprié té s des fonctions mesurables. Comptes Rendus Acad. Sci. Paris 154(1912), 1688–1690.Google Scholar
[34] Malý, J., A simple proof of the Stepanov theorem on differentiability almost everywhere. Exposition. Math. 17(1999), no. 1, 59–61.Google Scholar
[35] Malý, J. and L. Zajíček, , Approximate differentiation: Jarn´ık points. Fund. Math. 140(1991), no. 1, 87–97.CrossRefGoogle Scholar
[36] Miranda, M. Jr., Functions of bounded variation on “good” metric spaces. J. Math. Pures Appl. (9) 82(2003), no. 8, 975–1004.CrossRefGoogle Scholar
[37] Ranjbar-Motlagh, A., Generalized Stepanov type theorem with applications over metric-measure spaces. Houston J. Math. 34(2008), no. 2, 623–635.Google Scholar
[38] Semmes, S., Some novel types of fractal geometry. Oxford Mathematical Monographs, The Clarendon Press, Oxford University Press, New York, 2001.Google Scholar
[39] Shanmugalingam, N., Newtonian spaces: an extension of Sobolev spaces to metric spaces. Rev. Mat. Iberoamericana 16(2000), no. 2, 243–279. http://dx.doi.org/10.4171/RMI/275 CrossRefGoogle Scholar
[40] Stepanoff, W., Sur les conditions de l’existence de la différentielle totale. Rec. Math. Soc. Math. Moscou 32(1925), no. 3, 511–526.Google Scholar
[41] Whitney, H., On totally differentiable and smooth functions. Pacific J. Math. 1(1951), 143–159. http://dx.doi.org/10.2140/pjm.1951.1.143 CrossRefGoogle Scholar