1 Introduction
Let E be an elliptic curve defined over the rationals, and let
![]() $N_E$
denote the conductor of E. For a prime p not dividing
$N_E$
denote the conductor of E. For a prime p not dividing
![]() $N_E$
(called a good prime for E), we write
$N_E$
(called a good prime for E), we write
![]() $\widetilde {E}_p$
to denote the reduction of E modulo p. The curve
$\widetilde {E}_p$
to denote the reduction of E modulo p. The curve
![]() $\widetilde {E}_p$
is an elliptic curve over the finite field
$\widetilde {E}_p$
is an elliptic curve over the finite field
![]() $\mathbb {F}_p$
. Hence, the set of
$\mathbb {F}_p$
. Hence, the set of
![]() $\mathbb {F}_p$
-points, denoted
$\mathbb {F}_p$
-points, denoted
![]() $\widetilde {E}_p(\mathbb {F}_p)$
, forms a finite abelian group. It is well known that
$\widetilde {E}_p(\mathbb {F}_p)$
, forms a finite abelian group. It is well known that
for some positive integers
![]() $d_p(E)$
and
$d_p(E)$
and
![]() $e_p(E)$
such that
$e_p(E)$
such that
![]() $d_p(E) \mid e_p(E)$
.
$d_p(E) \mid e_p(E)$
.
There has been considerable interest, dating back to the 1970s, in studying the distribution of primes p for which
![]() $\widetilde {E}_p(\mathbb {F}_p)$
has certain properties. In particular, one defines a good prime p to be of cyclic reduction for E if
$\widetilde {E}_p(\mathbb {F}_p)$
has certain properties. In particular, one defines a good prime p to be of cyclic reduction for E if
![]() $\widetilde {E}_p(\mathbb {F}_p)$
is a cyclic group and of Koblitz reduction for E if
$\widetilde {E}_p(\mathbb {F}_p)$
is a cyclic group and of Koblitz reduction for E if
![]() $|\widetilde {E}_p(\mathbb {F}_p)|$
is a prime. It is worth noting that every prime p of Koblitz reduction is also of cyclic reduction, since every group of prime order is cyclic. Let
$|\widetilde {E}_p(\mathbb {F}_p)|$
is a prime. It is worth noting that every prime p of Koblitz reduction is also of cyclic reduction, since every group of prime order is cyclic. Let
![]() $\mathcal {X}$
be either “
$\mathcal {X}$
be either “
![]() $\operatorname {\mathrm {cyc}}$
” or “
$\operatorname {\mathrm {cyc}}$
” or “
![]() $\operatorname {\mathrm {prime}}$
” and
$\operatorname {\mathrm {prime}}$
” and
![]() $\mathcal {X}_E(p)$
be either “p is of cyclic reduction” or “p is of Koblitz reduction” for E, respectively. Define the counting function
$\mathcal {X}_E(p)$
be either “p is of cyclic reduction” or “p is of Koblitz reduction” for E, respectively. Define the counting function
The problem of determining asymptotics for
![]() $\pi _E^{\mathcal {X}}(x)$
is called the cyclicity problem or Koblitz problem, depending on the context. As noted in [Reference Balog, Cojocaru and David5, Reference Koblitz34], the Koblitz problem can be viewed as an elliptic curve analog of the twin prime conjecture.
$\pi _E^{\mathcal {X}}(x)$
is called the cyclicity problem or Koblitz problem, depending on the context. As noted in [Reference Balog, Cojocaru and David5, Reference Koblitz34], the Koblitz problem can be viewed as an elliptic curve analog of the twin prime conjecture.
It is natural to consider finer versions of the cyclicity and Koblitz problems which restrict to primes lying in arithmetic progressions. To discuss this, fix integers
![]() $n,k$
with
$n,k$
with
![]() $n \geq 1$
and define
$n \geq 1$
and define
Note that if n and k are not coprime, then there is at most one prime congruent to k modulo n, so
![]() $\pi _E^{\mathcal {X}}(x;n,k)$
is trivially bounded. As such, we will always take the integers n and k to be coprime. Broadly speaking, the goal of this article is to examine the constants that appear in the conjectural asymptotics of
$\pi _E^{\mathcal {X}}(x;n,k)$
is trivially bounded. As such, we will always take the integers n and k to be coprime. Broadly speaking, the goal of this article is to examine the constants that appear in the conjectural asymptotics of
![]() $\pi _E^{\mathcal {X}}(x;n,k)$
and explore how they are influenced by the choice of k modulo n. Before introducing our contributions, we outline aspects of the rich history of the cyclicity and Koblitz problems relevant to our work.
$\pi _E^{\mathcal {X}}(x;n,k)$
and explore how they are influenced by the choice of k modulo n. Before introducing our contributions, we outline aspects of the rich history of the cyclicity and Koblitz problems relevant to our work.
We begin with the cyclicity problem, which has its origin in 1975 when I. Borosh, C. J. Moreno, and H. Porta [Reference Borosh, Moreno and Porta9, pp. 962–963] speculated that the density of primes of cyclic reduction exists and can be expressed as an Euler product.Footnote 1 In 1976, J.-P. Serre [Reference Serre51] observed that the cyclicity problem bears a resemblance to Artin’s primitive root conjecture, which was proven under the Generalized Riemann hypothesis (GRH) by C. Hooley [Reference Hooley30] a decade prior. With this insight, Serre proposed the following conjecture, which he proved as a theorem under GRH.
Conjecture 1.1 (Cyclicity conjecture [Reference Serre51, pp. 465–468])
If
![]() $E/\mathbb {Q}$
is an elliptic curve, then
$E/\mathbb {Q}$
is an elliptic curve, then
as
![]() $x \to \infty $
, where
$x \to \infty $
, where
![]() $C^{\operatorname {\mathrm {cyc}}}_E \geq 0$
is the explicit constant defined in (18).
$C^{\operatorname {\mathrm {cyc}}}_E \geq 0$
is the explicit constant defined in (18).
Serre noted that
![]() $C^{\operatorname {\mathrm {cyc}}}_E = 0$
if and only if
$C^{\operatorname {\mathrm {cyc}}}_E = 0$
if and only if
![]() $\mathbb {Q}(E[2]) = \mathbb {Q}$
, in which case we interpret (1) as stating that
$\mathbb {Q}(E[2]) = \mathbb {Q}$
, in which case we interpret (1) as stating that
![]() $\pi _E^{\operatorname {\mathrm {cyc}}}(x)$
is bounded as
$\pi _E^{\operatorname {\mathrm {cyc}}}(x)$
is bounded as
![]() $x \to \infty $
.
$x \to \infty $
.
Conjecture 1.1 has been extensively studied by various mathematicians since then. M. Ram Murty [Reference Ram Murty46] proved that the conjecture holds unconditionally for CM curves. Later, using a lower bound sieve method, Gupta and Murty [Reference Gupta and Ram Murty28] showed unconditionally for non-CM curves that
as
![]() $x \to \infty $
unless
$x \to \infty $
unless
![]() $\mathbb {Q}(E[2]) = \mathbb {Q}$
. See, for example, [Reference Banks and Shparlinski6, Reference Campagna and Stevenhagen14–Reference Cojocaru16, Reference Fredericks24, Reference Jones31, Reference Wong59] for some recent work on the problem.
$\mathbb {Q}(E[2]) = \mathbb {Q}$
. See, for example, [Reference Banks and Shparlinski6, Reference Campagna and Stevenhagen14–Reference Cojocaru16, Reference Fredericks24, Reference Jones31, Reference Wong59] for some recent work on the problem.
In 2022, Y. Akbal and A. M. Güloğlu [Reference Akbal and Güloğlu1] studied the cyclicity problem for primes lying in an arithmetic progression. They proved that, under GRH,
as
![]() $x \to \infty $
, where
$x \to \infty $
, where
![]() $C^{\operatorname {\mathrm {cyc}}}_{E,n,k}$
is the explicit constant defined in (21). As before, if
$C^{\operatorname {\mathrm {cyc}}}_{E,n,k}$
is the explicit constant defined in (21). As before, if
![]() $C^{\operatorname {\mathrm {cyc}}}_{E,n,k} = 0$
, then we interpret (2) as stating that
$C^{\operatorname {\mathrm {cyc}}}_{E,n,k} = 0$
, then we interpret (2) as stating that
![]() $\pi _E^{\operatorname {\mathrm {cyc}}}(x;n,k)$
is bounded as
$\pi _E^{\operatorname {\mathrm {cyc}}}(x;n,k)$
is bounded as
![]() $x \to \infty $
. In 2015, J. Brau [Reference Brau12] obtained a formula for the constant
$x \to \infty $
. In 2015, J. Brau [Reference Brau12] obtained a formula for the constant
![]() $C^{\operatorname {\mathrm {cyc}}}_{E,n,k}$
for all Serre curves outside of a small class (see Remark 1.8). N. Jones and the first author [Reference Jones and Lee33] determined all the possible scenarios in which the constant
$C^{\operatorname {\mathrm {cyc}}}_{E,n,k}$
for all Serre curves outside of a small class (see Remark 1.8). N. Jones and the first author [Reference Jones and Lee33] determined all the possible scenarios in which the constant
![]() $C^{\operatorname {\mathrm {cyc}}}_{E,n,k}$
vanishes. Additionally, P. -J. Wong [Reference Wong60] established (2) unconditionally for CM elliptic curves.
$C^{\operatorname {\mathrm {cyc}}}_{E,n,k}$
vanishes. Additionally, P. -J. Wong [Reference Wong60] established (2) unconditionally for CM elliptic curves.
While Conjecture 1 remains open without assuming GRH, researchers have found success in proving the conjecture is true “on average” in various senses. As observed in [Reference Bell, Blakestad, Cojocaru, Cowan, Jones, Matei, Smith and Vogt8, Remark 7(v)], there are two broad approaches regarding the average results. One approach is to compute the density of elliptic curves E over
![]() $\mathbb {F}_p$
for which
$\mathbb {F}_p$
for which
![]() $E(\mathbb {F}_p)$
is cyclic, and average it over all primes p. Another approach is to count the number of primes for which an elliptic curve over
$E(\mathbb {F}_p)$
is cyclic, and average it over all primes p. Another approach is to count the number of primes for which an elliptic curve over
![]() $\mathbb {Q}$
has cyclic reduction and then average over the family of elliptic curves ordered by height. The former is called the “local” viewpoint while the latter is called the “global” viewpoint.
$\mathbb {Q}$
has cyclic reduction and then average over the family of elliptic curves ordered by height. The former is called the “local” viewpoint while the latter is called the “global” viewpoint.
In 1999, S. G. Vlăduţ [Reference Vlǎduţ57] obtained some statistics related to the cyclicity problem for elliptic curves over finite fields. In particular, he determined the ratio
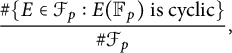 $$ \begin{align} \frac{\#\{E \in \mathcal{F}_p : E(\mathbb{F}_p)\text{ is cyclic}\}}{\#\mathcal{F}_p}, \end{align} $$
$$ \begin{align} \frac{\#\{E \in \mathcal{F}_p : E(\mathbb{F}_p)\text{ is cyclic}\}}{\#\mathcal{F}_p}, \end{align} $$
where
![]() $\mathcal {F}_p$
denotes the set of isomorphism classes of elliptic curves over
$\mathcal {F}_p$
denotes the set of isomorphism classes of elliptic curves over
![]() $\mathbb {F}_p$
. Later, E.-U. Gekeler [Reference Gekeler26] built upon this result to obtain the local result for the average cyclicity problem. He computed that the average of (3) over all primes p is
$\mathbb {F}_p$
. Later, E.-U. Gekeler [Reference Gekeler26] built upon this result to obtain the local result for the average cyclicity problem. He computed that the average of (3) over all primes p is
![]() $C^{\operatorname {\mathrm {cyc}}}$
, which is defined in (20).
$C^{\operatorname {\mathrm {cyc}}}$
, which is defined in (20).
In 2009, building upon Vlăduţ’s work, W. D. Banks and I. E. Shparlinski [Reference Banks and Shparlinski6] deduced a global result for the average cyclicity problem and demonstrated that it aligns with Gekeler’s local result. To set notation: For positive real numbers A and B, let ![]() denote the family of elliptic curves
denote the family of elliptic curves
![]() $E/\mathbb {Q}$
defined by a short Weierstrass model
$E/\mathbb {Q}$
defined by a short Weierstrass model
for some
![]() $a,b \in \mathbb {Z}$
satisfying
$a,b \in \mathbb {Z}$
satisfying
![]() $|a| \leq A$
and
$|a| \leq A$
and
![]() $|b|\leq B$
. Banks and Shparlinski proved the following.
$|b|\leq B$
. Banks and Shparlinski proved the following.
Theorem 1.2 [Reference Banks and Shparlinski6, Theorem 18]
Let
![]() $x> 0$
and
$x> 0$
and
![]() $\epsilon>0$
. Let
$\epsilon>0$
. Let ![]() and
and ![]() be parameters satisfying
be parameters satisfying
![]() $x^{\epsilon } \leq A, B \leq x^{1-\epsilon },$
and
$x^{\epsilon } \leq A, B \leq x^{1-\epsilon },$
and
![]() $AB \geq x^{1+\epsilon }$
. Then, we have
$AB \geq x^{1+\epsilon }$
. Then, we have
Later, the inequality conditions on A and B in the theorem above were significantly relaxed by A. Akbary and A. T. Felix [Reference Akbary and Felix2, Corollary 1.5].
Building upon Banks and Shparlinski’s methods, the first author refined the results to consider primes in arithmetic progressions [Reference Lee38, Theorem 1.3]. To summarize his results, under the same assumptions of Theorem 1.2, for
![]() $n \leq \log x$
and k coprime to n, there exists a positive constant
$n \leq \log x$
and k coprime to n, there exists a positive constant
![]() $ C^{\operatorname {\mathrm {cyc}}}_{n,k}$
for which
$ C^{\operatorname {\mathrm {cyc}}}_{n,k}$
for which
The average constant
![]() $C^{\operatorname {\mathrm {cyc}}}_{n,k}$
is given explicitly in (23).
$C^{\operatorname {\mathrm {cyc}}}_{n,k}$
is given explicitly in (23).
Related to the cyclicity problem is the Koblitz problem, which seeks to understand the asymptotics of
![]() $\pi _E^{\operatorname {\mathrm {prime}}}(x)$
and has significance for elliptic curve cryptography [Reference Savaş, Schmidt and Koç47, Reference Stevenhagen55]. In 1988, N. Koblitz [Reference Koblitz34] made a conjecture analogous to Conjecture 1.1. In particular, it follows from the conjecture that a non-CM elliptic curve
$\pi _E^{\operatorname {\mathrm {prime}}}(x)$
and has significance for elliptic curve cryptography [Reference Savaş, Schmidt and Koç47, Reference Stevenhagen55]. In 1988, N. Koblitz [Reference Koblitz34] made a conjecture analogous to Conjecture 1.1. In particular, it follows from the conjecture that a non-CM elliptic curve
![]() $E/\mathbb {Q}$
has infinitely many primes of Koblitz reduction unless E is rationally isogenous to an elliptic curve with nontrivial rational torsion. The Koblitz conjecture remained open for over 20 years until Jones gave a counterexample, which appears in [Reference Zywina62, Section 1.1]. The fundamental issue with the conjecture, which the counterexample exploits, is its failure to account for the possibility of entanglements of division fields. Properly accounting for this possibility, D. Zywina [Reference Zywina62] refined the Koblitz conjecture as follows.
$E/\mathbb {Q}$
has infinitely many primes of Koblitz reduction unless E is rationally isogenous to an elliptic curve with nontrivial rational torsion. The Koblitz conjecture remained open for over 20 years until Jones gave a counterexample, which appears in [Reference Zywina62, Section 1.1]. The fundamental issue with the conjecture, which the counterexample exploits, is its failure to account for the possibility of entanglements of division fields. Properly accounting for this possibility, D. Zywina [Reference Zywina62] refined the Koblitz conjecture as follows.
Conjecture 1.3 (Refined Koblitz conjecture, [Reference Zywina62, Conjecture 1.2])
If
![]() $E/\mathbb {Q}$
is an elliptic curve, then
$E/\mathbb {Q}$
is an elliptic curve, then
as
![]() $x \to \infty $
, where
$x \to \infty $
, where
![]() $C_{E}^{\operatorname {\mathrm {prime}}}\geq 0$
is the explicit constant defined in (27).
$C_{E}^{\operatorname {\mathrm {prime}}}\geq 0$
is the explicit constant defined in (27).
Similar to the cyclicity case, the constant
![]() $C^{\operatorname {\mathrm {prime}}}_E$
may vanish. In this case, we interpret (5) as indicating that
$C^{\operatorname {\mathrm {prime}}}_E$
may vanish. In this case, we interpret (5) as indicating that
![]() $\pi _E^{\operatorname {\mathrm {prime}}}(x)$
is bounded as
$\pi _E^{\operatorname {\mathrm {prime}}}(x)$
is bounded as
![]() $x\to \infty $
. Beyond the statement of the conjecture provided above, Zywina made the conjecture more generally for elliptic curves over number fields and allowed for a parameter t to consider primes p for which
$x\to \infty $
. Beyond the statement of the conjecture provided above, Zywina made the conjecture more generally for elliptic curves over number fields and allowed for a parameter t to consider primes p for which
![]() $|\widetilde {E}_p(\mathbb {F}_p)|/t$
is prime.
$|\widetilde {E}_p(\mathbb {F}_p)|/t$
is prime.
Conjecture 1.3 is often referred to as an elliptic curve analog of the twin prime conjecture. Assuming that the events “p is prime” and “
![]() $|\widetilde {E}_p(\mathbb {F}_p)|$
is prime” are independent, and applying the Hardy–Littlewood heuristic [Reference Hardy and Littlewood29], one would expect that
$|\widetilde {E}_p(\mathbb {F}_p)|$
is prime” are independent, and applying the Hardy–Littlewood heuristic [Reference Hardy and Littlewood29], one would expect that
![]() $\pi _E^{\operatorname {\mathrm {prime}}}(x)$
should grow like a constant times
$\pi _E^{\operatorname {\mathrm {prime}}}(x)$
should grow like a constant times
![]() $x/\log ^2 x$
, unless E has an intrinsic obstruction preventing the existence of primes of Koblitz reduction. Although Conjecture 1.3 remains open even under GRH, upper bounds for
$x/\log ^2 x$
, unless E has an intrinsic obstruction preventing the existence of primes of Koblitz reduction. Although Conjecture 1.3 remains open even under GRH, upper bounds for
![]() $\pi _E^{\operatorname {\mathrm {prime}}}(x)$
have been studied by several authors. A notable result is due to A. C. Cojocaru [Reference Cojocaru18], who proved that for a non-CM
$\pi _E^{\operatorname {\mathrm {prime}}}(x)$
have been studied by several authors. A notable result is due to A. C. Cojocaru [Reference Cojocaru18], who proved that for a non-CM
![]() $E/\mathbb {Q}$
of conductor
$E/\mathbb {Q}$
of conductor
![]() $N_E$
, we have
$N_E$
, we have
as
![]() $x \to \infty $
, under the quasi-GRH. (See [Reference Cojocaru18, p. 268].) For CM curves, she applied Selberg’s sieve to prove that the upper bound holds unconditionally, independently of the conductor. Later, C. David and J. Wu [Reference David and Wu22] improved (6) into an effective upper bound for non-CM curves under the quasi-GRH. However, a lower bound for
$x \to \infty $
, under the quasi-GRH. (See [Reference Cojocaru18, p. 268].) For CM curves, she applied Selberg’s sieve to prove that the upper bound holds unconditionally, independently of the conductor. Later, C. David and J. Wu [Reference David and Wu22] improved (6) into an effective upper bound for non-CM curves under the quasi-GRH. However, a lower bound for
![]() $\pi _E^{\operatorname {\mathrm {prime}}}(x)$
remains unknown.
$\pi _E^{\operatorname {\mathrm {prime}}}(x)$
remains unknown.
A related problem is to understand how many prime factors the group order
![]() $|\widetilde {E}_p(\mathbb {F}_p)|$
has as p varies. One of the first major advances in this direction was made by S. A. Miri and V. K. Murty [Reference Ali Miri and Kumar Murty3]. Given a positive integer N, let
$|\widetilde {E}_p(\mathbb {F}_p)|$
has as p varies. One of the first major advances in this direction was made by S. A. Miri and V. K. Murty [Reference Ali Miri and Kumar Murty3]. Given a positive integer N, let
![]() $\nu (N)$
denote the number of prime factors of N, counted with multiplicity. They demonstrated that, assuming GRH, for any non-CM elliptic curve
$\nu (N)$
denote the number of prime factors of N, counted with multiplicity. They demonstrated that, assuming GRH, for any non-CM elliptic curve
![]() $E/\mathbb {Q}$
,
$E/\mathbb {Q}$
,
as
![]() $x \to \infty $
. This line of research was continued by many mathematicians, leading to successive improvements: the bound of 16 was reduced to 8 for non-CM curves under GRH, and to 5 for CM curves unconditionally (see, for example, [Reference Cojocaru18, Reference David and Wu22, Reference Steuding and Weng54]).
$x \to \infty $
. This line of research was continued by many mathematicians, leading to successive improvements: the bound of 16 was reduced to 8 for non-CM curves under GRH, and to 5 for CM curves unconditionally (see, for example, [Reference Cojocaru18, Reference David and Wu22, Reference Steuding and Weng54]).
In 2011, A. Balog, A. C. Cojocaru, and C. David obtained a local result for the average version of the Koblitz problem and applied it to deduce the following global results.
Theorem 1.4 [Reference Balog, Cojocaru and David5, Theorem 1]
Set
![]() $x> 0$
and
$x> 0$
and
![]() $\epsilon> 0$
. Let
$\epsilon> 0$
. Let ![]() and
and ![]() be parameters satisfying
be parameters satisfying
![]() $x^{\epsilon } < A,B$
and
$x^{\epsilon } < A,B$
and
![]() $AB> x\log ^{10}x$
. There exists a constant
$AB> x\log ^{10}x$
. There exists a constant
![]() $C^{\operatorname {\mathrm {prime}}}> 0$
for which
$C^{\operatorname {\mathrm {prime}}}> 0$
for which
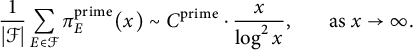 $$ \begin{align*}\frac{1}{|\mathcal{F}|} \sum_{E\in \mathcal{F}} \pi_E^{\operatorname{\mathrm{prime}}}(x) \sim C^{\operatorname{\mathrm{prime}}} \cdot \frac{x}{\log^2 x}, \hspace{0.5cm} \text{ as } x\to \infty.\end{align*} $$
$$ \begin{align*}\frac{1}{|\mathcal{F}|} \sum_{E\in \mathcal{F}} \pi_E^{\operatorname{\mathrm{prime}}}(x) \sim C^{\operatorname{\mathrm{prime}}} \cdot \frac{x}{\log^2 x}, \hspace{0.5cm} \text{ as } x\to \infty.\end{align*} $$
The average constant
![]() $C^{\operatorname {\mathrm {prime}}}$
is defined in (33). The inequality conditions on A and B can also be relaxed as in Akbary and Felix [Reference Akbary and Felix2, Equation (1.8)].
$C^{\operatorname {\mathrm {prime}}}$
is defined in (33). The inequality conditions on A and B can also be relaxed as in Akbary and Felix [Reference Akbary and Felix2, Equation (1.8)].
A natural inquiry is whether each of these average results is consistent with the corresponding conjectured outcomes on average. This question was answered by Jones [Reference Jones31], assuming an affirmative answer to Serre’s uniformity question (Question 2.3).
Theorem 1.5 [Reference Jones31, Theorem 6]
Assume an affirmative answer to Serre’s uniformity question. Let
![]() $\mathcal {X} \in \{\operatorname {\mathrm {cyc}}, \operatorname {\mathrm {prime}}\}$
. There exists an exponent
$\mathcal {X} \in \{\operatorname {\mathrm {cyc}}, \operatorname {\mathrm {prime}}\}$
. There exists an exponent
![]() $\gamma> 0$
such that for any positive integer t, we have
$\gamma> 0$
such that for any positive integer t, we have
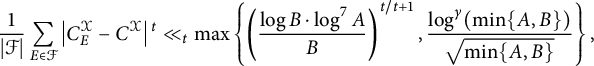 $$ \begin{align*}\frac{1}{|\mathcal{F}|} \sum_{E \in \mathcal{F}} \left|C_E^{\mathcal{X}}-C^{\mathcal{X}}\right|{}^t \ll_t \max \left\{\left(\frac{\log B \cdot \log^7 A}{B}\right)^{t/t+1}, \frac{\log^{\gamma}(\min\{A,B\})}{\sqrt{\min\{A,B\}}} \right\},\end{align*} $$
$$ \begin{align*}\frac{1}{|\mathcal{F}|} \sum_{E \in \mathcal{F}} \left|C_E^{\mathcal{X}}-C^{\mathcal{X}}\right|{}^t \ll_t \max \left\{\left(\frac{\log B \cdot \log^7 A}{B}\right)^{t/t+1}, \frac{\log^{\gamma}(\min\{A,B\})}{\sqrt{\min\{A,B\}}} \right\},\end{align*} $$
as
![]() $\min \{A,B\} \to \infty $
.
$\min \{A,B\} \to \infty $
.
In particular, by taking
![]() $t = 1$
, Theorem 1.5 gives a result on the average value of the constants
$t = 1$
, Theorem 1.5 gives a result on the average value of the constants
![]() $C_{E}^{\mathcal {X}}$
. Indeed, suppose that
$C_{E}^{\mathcal {X}}$
. Indeed, suppose that ![]() and
and ![]() tend to infinity as
tend to infinity as
![]() $x \to \infty $
and assume an affirmative answer to Serre’s uniformity question and that
$x \to \infty $
and assume an affirmative answer to Serre’s uniformity question and that
![]() $(\log B \log ^7 A)/B \to 0$
as
$(\log B \log ^7 A)/B \to 0$
as
![]() $x \to \infty $
. Then for
$x \to \infty $
. Then for
![]() $\mathcal {X} \in \{\operatorname {\mathrm {cyc}}, \operatorname {\mathrm {prime}}\}$
, we have
$\mathcal {X} \in \{\operatorname {\mathrm {cyc}}, \operatorname {\mathrm {prime}}\}$
, we have
This verifies that the average of the constants
![]() $C^{\mathcal {X}}_E$
aligns with the average constants
$C^{\mathcal {X}}_E$
aligns with the average constants
![]() $C^{\mathcal {X}}$
.
$C^{\mathcal {X}}$
.
In this article, we utilize Zywina’s approach to propose the Koblitz constant
![]() $C^{\operatorname {\mathrm {prime}}}_{E,n,k}$
for primes in arithmetic progressions. Unlike the cyclicity problem, the average version of the Koblitz constant
$C^{\operatorname {\mathrm {prime}}}_{E,n,k}$
for primes in arithmetic progressions. Unlike the cyclicity problem, the average version of the Koblitz constant
![]() $C^{\operatorname {\mathrm {prime}}}_{E,n,k}$
has not yet been considered. We address this gap in the literature by providing a candidate for
$C^{\operatorname {\mathrm {prime}}}_{E,n,k}$
has not yet been considered. We address this gap in the literature by providing a candidate for
![]() $C^{\operatorname {\mathrm {prime}}}_{n,k}$
, the average version of
$C^{\operatorname {\mathrm {prime}}}_{n,k}$
, the average version of
![]() $C^{\operatorname {\mathrm {prime}}}_{E,n,k}$
, in (42). We illustrate the suitability of these conjectural constants by proving an analogous version of Theorem 1.5 for them.
$C^{\operatorname {\mathrm {prime}}}_{E,n,k}$
, in (42). We illustrate the suitability of these conjectural constants by proving an analogous version of Theorem 1.5 for them.
We start by formulating the Koblitz conjecture for primes in arithmetic progressions.
Conjecture 1.6 If
![]() $E/\mathbb {Q}$
is an elliptic curve, then there exists
$E/\mathbb {Q}$
is an elliptic curve, then there exists
![]() $C^{\operatorname {\mathrm {prime}}}_{E,n,k} \geq 0$
for which
$C^{\operatorname {\mathrm {prime}}}_{E,n,k} \geq 0$
for which
as
![]() $x \to \infty $
, where
$x \to \infty $
, where
![]() $C^{\operatorname {\mathrm {prime}}}_{E,n,k}$
is the explicit constant defined in (35).
$C^{\operatorname {\mathrm {prime}}}_{E,n,k}$
is the explicit constant defined in (35).
As before, if
![]() $C^{\operatorname {\mathrm {prime}}}_{E,n,k} = 0$
, we interpret the above as saying that
$C^{\operatorname {\mathrm {prime}}}_{E,n,k} = 0$
, we interpret the above as saying that
![]() $\pi ^{\operatorname {\mathrm {prime}}}_{E}(x;n,k)$
is bounded as
$\pi ^{\operatorname {\mathrm {prime}}}_{E}(x;n,k)$
is bounded as
![]() $x \to \infty $
. As one piece of evidence to suggest
$x \to \infty $
. As one piece of evidence to suggest
![]() $C^{\operatorname {\mathrm {prime}}}_{n,k}$
is the correct average constant, we compare it with the constant
$C^{\operatorname {\mathrm {prime}}}_{n,k}$
is the correct average constant, we compare it with the constant
![]() $C^{\operatorname {\mathrm {prime}}}_{E, n,k}$
for Serre curves which, by Jones [Reference Jones32], make up a density 1 set of elliptic curves when ordered by naive height.
$C^{\operatorname {\mathrm {prime}}}_{E, n,k}$
for Serre curves which, by Jones [Reference Jones32], make up a density 1 set of elliptic curves when ordered by naive height.
To state our theorem, we first introduce some notation. Associated with E, we define the constant
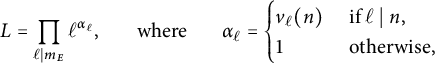 $$ \begin{align} L = \prod_{\ell \mid m_E} \ell^{\alpha_\ell}, \hspace{0.5cm} \text{ where } \hspace{0.5cm} \alpha_\ell = \begin{cases} v_\ell(n) & \text{ if } \ell \mid n, \\ 1 & \text{ otherwise}, \end{cases} \end{align} $$
$$ \begin{align} L = \prod_{\ell \mid m_E} \ell^{\alpha_\ell}, \hspace{0.5cm} \text{ where } \hspace{0.5cm} \alpha_\ell = \begin{cases} v_\ell(n) & \text{ if } \ell \mid n, \\ 1 & \text{ otherwise}, \end{cases} \end{align} $$
where
![]() $m_E$
denotes the adelic level of E (defined in Sections 2.1 and 2.3) and
$m_E$
denotes the adelic level of E (defined in Sections 2.1 and 2.3) and
![]() $v_\ell (n)$
denotes the
$v_\ell (n)$
denotes the
![]() $\ell $
-adic valuation of n. The constants
$\ell $
-adic valuation of n. The constants
![]() $m_E$
and L play a crucial role in computing
$m_E$
and L play a crucial role in computing
![]() $C^{\operatorname {\mathrm {cyc}}}_{E,n,k}$
and
$C^{\operatorname {\mathrm {cyc}}}_{E,n,k}$
and
![]() $C^{\operatorname {\mathrm {prime}}}_{E,n,k}$
. For a Serre curve E, Proposition 2.4 gives a straightforward formula for
$C^{\operatorname {\mathrm {prime}}}_{E,n,k}$
. For a Serre curve E, Proposition 2.4 gives a straightforward formula for
![]() $m_E$
,
$m_E$
,
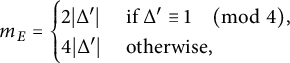 $$ \begin{align*}m_E = \begin{cases} 2|\Delta'| & \text{ if } \Delta^{\prime} \equiv 1 \quad\pmod 4, \\ 4|\Delta^{\prime}| & \text{ otherwise}, \end{cases} \end{align*} $$
$$ \begin{align*}m_E = \begin{cases} 2|\Delta'| & \text{ if } \Delta^{\prime} \equiv 1 \quad\pmod 4, \\ 4|\Delta^{\prime}| & \text{ otherwise}, \end{cases} \end{align*} $$
where
![]() $\Delta ^{\prime }$
denotes the squarefree part of the discriminant
$\Delta ^{\prime }$
denotes the squarefree part of the discriminant
![]() $\Delta _E$
of any Weierstrass model of E.
$\Delta _E$
of any Weierstrass model of E.
Theorem 1.7 Let
![]() $E/\mathbb {Q}$
be a Serre curve and let
$E/\mathbb {Q}$
be a Serre curve and let
![]() $m_E$
,
$m_E$
,
![]() $\Delta ^{\prime }$
, and L be as above. If
$\Delta ^{\prime }$
, and L be as above. If
![]() $m_E \nmid L,$
then
$m_E \nmid L,$
then
Otherwise, if
![]() $m_E \mid L$
, then
$m_E \mid L$
, then
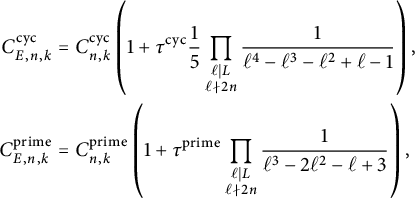 $$ \begin{align*} C^{\operatorname{\mathrm{cyc}}}_{E,n,k} &= C^{\operatorname{\mathrm{cyc}}}_{n,k} \left( 1 + \tau^{\operatorname{\mathrm{cyc}}} \frac{1}{5} \prod_{\substack{\ell \mid L \\ \ell \nmid 2n}} \frac{1}{\ell^4-\ell^3-\ell^2+\ell-1} \right), \\ C^{\operatorname{\mathrm{prime}}}_{E,n,k} &= C^{\operatorname{\mathrm{prime}}}_{n,k} \left( 1 + \tau^{\operatorname{\mathrm{prime}}}\prod_{\substack{\ell \mid L \\\ell \nmid 2n}} \frac{1}{\ell^3-2 \ell^2-\ell+3}\right), \end{align*} $$
$$ \begin{align*} C^{\operatorname{\mathrm{cyc}}}_{E,n,k} &= C^{\operatorname{\mathrm{cyc}}}_{n,k} \left( 1 + \tau^{\operatorname{\mathrm{cyc}}} \frac{1}{5} \prod_{\substack{\ell \mid L \\ \ell \nmid 2n}} \frac{1}{\ell^4-\ell^3-\ell^2+\ell-1} \right), \\ C^{\operatorname{\mathrm{prime}}}_{E,n,k} &= C^{\operatorname{\mathrm{prime}}}_{n,k} \left( 1 + \tau^{\operatorname{\mathrm{prime}}}\prod_{\substack{\ell \mid L \\\ell \nmid 2n}} \frac{1}{\ell^3-2 \ell^2-\ell+3}\right), \end{align*} $$
where
![]() $\tau ^{\operatorname {\mathrm {cyc}}},\tau ^{\operatorname {\mathrm {prime}}} \in \{\pm 1\}$
are defined in Definition 5.1.
$\tau ^{\operatorname {\mathrm {cyc}}},\tau ^{\operatorname {\mathrm {prime}}} \in \{\pm 1\}$
are defined in Definition 5.1.
Remark 1.8 For a Serre curve E, the constant
![]() $C^{\operatorname {\mathrm {cyc}}}_{E,n,k}$
was previously obtained by Brau [Reference Brau12, Proposition 2.5.8] under the assumption that
$C^{\operatorname {\mathrm {cyc}}}_{E,n,k}$
was previously obtained by Brau [Reference Brau12, Proposition 2.5.8] under the assumption that
![]() $\Delta ^{\prime } \not \in \{-2,-1,2\}$
. Our formula for
$\Delta ^{\prime } \not \in \{-2,-1,2\}$
. Our formula for
![]() $C^{\operatorname {\mathrm {cyc}}}_{E,n,k}$
does not require this assumption and it aligns with Brau’s.
$C^{\operatorname {\mathrm {cyc}}}_{E,n,k}$
does not require this assumption and it aligns with Brau’s.
As another piece of evidence, we also consider the moments of the constants
![]() $C^{\operatorname {\mathrm {cyc}}}_{E, n, k}$
and
$C^{\operatorname {\mathrm {cyc}}}_{E, n, k}$
and
![]() $C^{\operatorname {\mathrm {prime}}}_{E, n, k}$
for
$C^{\operatorname {\mathrm {prime}}}_{E, n, k}$
for
![]() $E\in \mathcal {F}$
. Building upon Jones’s methods, we improve Theorem 1.5 unconditionally as follows.
$E\in \mathcal {F}$
. Building upon Jones’s methods, we improve Theorem 1.5 unconditionally as follows.
Theorem 1.9 Let n be a positive integer and k be coprime to n. Then there exists an exponent
![]() $\gamma> 0$
such that for any positive integer t, we have
$\gamma> 0$
such that for any positive integer t, we have
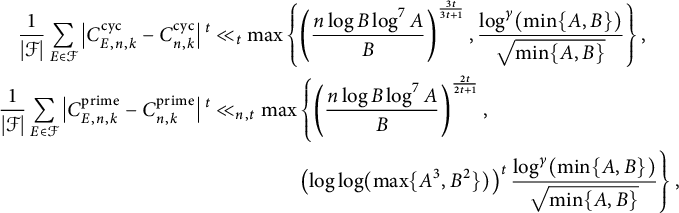 $$ \begin{align*} \frac{1}{|\mathcal{F}|} \sum_{E\in \mathcal{F}} \left|C^{\mathcal{\operatorname{\mathrm{cyc}}}}_{E,n,k} - C^{\operatorname{\mathrm{cyc}}}_{n,k} \right|{}^t &\ll_t \max \left\{ \left( \frac{n \log B \log^7 A}{B}\right)^{\frac{3t}{3t+1}}, \frac{\log^\gamma (\min\{A,B\})}{\sqrt{\min\{A,B\}}} \right\}, \\ \frac{1}{|\mathcal{F}|} \sum_{E\in \mathcal{F}} \left|C^{\operatorname{\mathrm{prime}}}_{E,n,k} - C^{\operatorname{\mathrm{prime}}}_{n,k}\right|{}^t &\ll_{n,t} \max \left\{ \left( \frac{n \log B \log^7 A}{B}\right)^{\frac{2t}{2t+1}},\right.\\ &\qquad\qquad\left.\left(\log \log (\max\{A^3,B^2\})\right)^t \frac{\log^\gamma (\min\{A,B\})}{\sqrt{\min\{A,B\}}} \right\}, \end{align*} $$
$$ \begin{align*} \frac{1}{|\mathcal{F}|} \sum_{E\in \mathcal{F}} \left|C^{\mathcal{\operatorname{\mathrm{cyc}}}}_{E,n,k} - C^{\operatorname{\mathrm{cyc}}}_{n,k} \right|{}^t &\ll_t \max \left\{ \left( \frac{n \log B \log^7 A}{B}\right)^{\frac{3t}{3t+1}}, \frac{\log^\gamma (\min\{A,B\})}{\sqrt{\min\{A,B\}}} \right\}, \\ \frac{1}{|\mathcal{F}|} \sum_{E\in \mathcal{F}} \left|C^{\operatorname{\mathrm{prime}}}_{E,n,k} - C^{\operatorname{\mathrm{prime}}}_{n,k}\right|{}^t &\ll_{n,t} \max \left\{ \left( \frac{n \log B \log^7 A}{B}\right)^{\frac{2t}{2t+1}},\right.\\ &\qquad\qquad\left.\left(\log \log (\max\{A^3,B^2\})\right)^t \frac{\log^\gamma (\min\{A,B\})}{\sqrt{\min\{A,B\}}} \right\}, \end{align*} $$
as
![]() $\min \{A,B\} \to \infty $
.
$\min \{A,B\} \to \infty $
.
Observe that as
![]() $\min \{A,B\} \to \infty $
, we have
$\min \{A,B\} \to \infty $
, we have
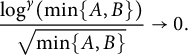 $$ \begin{align*}\frac{\log^\gamma (\min\{A,B\})}{\sqrt{\min\{A,B\}}} \to 0.\end{align*} $$
$$ \begin{align*}\frac{\log^\gamma (\min\{A,B\})}{\sqrt{\min\{A,B\}}} \to 0.\end{align*} $$
This gives us the following corollary.
Corollary 1.10 Fix
![]() $n\in \mathbb {N}$
. Let k be coprime to n. Let
$n\in \mathbb {N}$
. Let k be coprime to n. Let ![]() and
and ![]() both tend to infinity as
both tend to infinity as
![]() $x \to \infty $
. With the same notation as in Theorem 1.9 and for
$x \to \infty $
. With the same notation as in Theorem 1.9 and for
![]() $\mathcal {X} \in \{\operatorname {\mathrm {cyc}}, \operatorname {\mathrm {prime}}\}$
, we have that
$\mathcal {X} \in \{\operatorname {\mathrm {cyc}}, \operatorname {\mathrm {prime}}\}$
, we have that
provided that as
![]() $x\to \infty $
,
$x\to \infty $
,
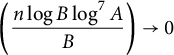 $$ \begin{align*}\left( \frac{n \log B \log^7 A}{B}\right) \to 0\end{align*} $$
$$ \begin{align*}\left( \frac{n \log B \log^7 A}{B}\right) \to 0\end{align*} $$
in the cyclicity case and
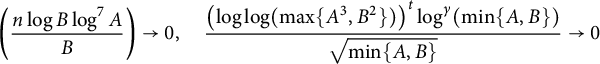 $$ \begin{align*}\left( \frac{n \log B \log^7 A}{B}\right) \to 0, \quad \frac{\left(\log \log (\max\{A^3,B^2\})\right)^t \log^\gamma (\min\{A,B\})}{\sqrt{\min\{A,B\}}} \to 0\end{align*} $$
$$ \begin{align*}\left( \frac{n \log B \log^7 A}{B}\right) \to 0, \quad \frac{\left(\log \log (\max\{A^3,B^2\})\right)^t \log^\gamma (\min\{A,B\})}{\sqrt{\min\{A,B\}}} \to 0\end{align*} $$
in the Koblitz case.
Based on the above considerations, the constant
![]() $C^{\operatorname {\mathrm {prime}}}_{n,k}$
that we propose in this article appears to be a plausible candidate for the average counterpart of
$C^{\operatorname {\mathrm {prime}}}_{n,k}$
that we propose in this article appears to be a plausible candidate for the average counterpart of
![]() $C^{\operatorname {\mathrm {prime}}}_{E,n,k}$
.
$C^{\operatorname {\mathrm {prime}}}_{E,n,k}$
.
The average constants
![]() $C^{\operatorname {\mathrm {cyc}}}_{n,k}$
and
$C^{\operatorname {\mathrm {cyc}}}_{n,k}$
and
![]() $C^{\operatorname {\mathrm {prime}}}_{n,k}$
are given explicitly and we can compute their values (to any given precision) using the Magma [Reference Bosma, Cannon and Playoust10] scripts available in this article’s GitHub repository [Reference Lee, Mayle and Wang39]. Below are tables with the values of
$C^{\operatorname {\mathrm {prime}}}_{n,k}$
are given explicitly and we can compute their values (to any given precision) using the Magma [Reference Bosma, Cannon and Playoust10] scripts available in this article’s GitHub repository [Reference Lee, Mayle and Wang39]. Below are tables with the values of
![]() $C^{\mathcal {X}}_{n,k}$
for
$C^{\mathcal {X}}_{n,k}$
for
![]() $\mathcal {X} \in \{\operatorname {\mathrm {cyc}}, \operatorname {\mathrm {prime}}\}$
and small moduli n.
$\mathcal {X} \in \{\operatorname {\mathrm {cyc}}, \operatorname {\mathrm {prime}}\}$
and small moduli n.
Table 1: The value of
![]() $C_{n,k}^{\operatorname {\mathrm {cyc}}}$
to six decimal places.
$C_{n,k}^{\operatorname {\mathrm {cyc}}}$
to six decimal places.

Table 2: The value of
![]() $C_{n,k}^{\operatorname {\mathrm {prime}}}$
to six decimal places.
$C_{n,k}^{\operatorname {\mathrm {prime}}}$
to six decimal places.

From the table, we observe that
![]() $C^{\mathcal {X}}_{2,1}=C^{\mathcal {X}}$
. Moreover, in each table, the sum of the values across any given row yields
$C^{\mathcal {X}}_{2,1}=C^{\mathcal {X}}$
. Moreover, in each table, the sum of the values across any given row yields
![]() $C^{\mathcal {X}}$
. In Propositions 4.1 and 4.6, we prove (reassuringly) that these simple checks hold for all moduli.
$C^{\mathcal {X}}$
. In Propositions 4.1 and 4.6, we prove (reassuringly) that these simple checks hold for all moduli.
Let p be a good prime for E. As noted previously,
Hence, for an arbitrary elliptic curve
![]() $E/\mathbb {Q}$
, one might suspect that if primes in a certain congruence class are more likely to be primes of Koblitz reduction, then they are also more likely to be primes of cyclic reduction. However, the tables above suggest that the contrary holds on average. Indeed, it follows from the formulas (23) and (42) for
$E/\mathbb {Q}$
, one might suspect that if primes in a certain congruence class are more likely to be primes of Koblitz reduction, then they are also more likely to be primes of cyclic reduction. However, the tables above suggest that the contrary holds on average. Indeed, it follows from the formulas (23) and (42) for
![]() $C^{\mathcal {X}}_{n,k}$
that these two average constants are oppositely biased for any given modulus n. More specifically, for any k coprime to n, we have
$C^{\mathcal {X}}_{n,k}$
that these two average constants are oppositely biased for any given modulus n. More specifically, for any k coprime to n, we have
Furthermore, we have
![]() $C^{\operatorname {\mathrm {cyc}}}_{n,1} < C^{\operatorname {\mathrm {cyc}}}_{n,-1}$
and
$C^{\operatorname {\mathrm {cyc}}}_{n,1} < C^{\operatorname {\mathrm {cyc}}}_{n,-1}$
and
![]() $C^{\operatorname {\mathrm {prime}}}_{n,1}> C^{\operatorname {\mathrm {prime}}}_{n,-1}$
if and only if n is not a power of two. The phenomenon of primes being statistically biased over congruence classes is referred to as the average congruence class bias and was first observed in the cyclicity problem by the first author in [Reference Lee38].
$C^{\operatorname {\mathrm {prime}}}_{n,1}> C^{\operatorname {\mathrm {prime}}}_{n,-1}$
if and only if n is not a power of two. The phenomenon of primes being statistically biased over congruence classes is referred to as the average congruence class bias and was first observed in the cyclicity problem by the first author in [Reference Lee38].
Lastly, it is notable that in both tables,
![]() $C^{\mathcal {X}}_{5,2} = C^{\mathcal {X}}_{5,3} = C^{\mathcal {X}}_{5,4}$
. This is because, for a fixed n, the value of
$C^{\mathcal {X}}_{5,2} = C^{\mathcal {X}}_{5,3} = C^{\mathcal {X}}_{5,4}$
. This is because, for a fixed n, the value of
![]() $C^{\mathcal {X}}_{n,k}$
depends solely on whether k is congruent to
$C^{\mathcal {X}}_{n,k}$
depends solely on whether k is congruent to
![]() $1$
or not modulo each prime factor of n. Therefore, for a fixed modulus n that is supported by s distinct odd primes, there are at most
$1$
or not modulo each prime factor of n. Therefore, for a fixed modulus n that is supported by s distinct odd primes, there are at most
![]() $2^s$
distinct values of
$2^s$
distinct values of
![]() $C^{\mathcal {X}}_{n,k}$
. Whether there are exactly
$C^{\mathcal {X}}_{n,k}$
. Whether there are exactly
![]() $2^s$
distinct values is a question proposed by the first author in [Reference Lee38].
$2^s$
distinct values is a question proposed by the first author in [Reference Lee38].
1.1 Outline of the article
Sections 2 and 3 provide the essential groundwork for proving the main results. In Section 2, we introduce the properties of Galois representations of elliptic curves. In particular, we introduce the definition of the adelic level and characterize the Galois images of Serre curves and CM curves. In Section 3, we determine the sizes of certain subsets of matrix groups that will be used in calculating the Euler factors of product expansions of
![]() $C_{E, n, k}^{\operatorname {\mathrm {cyc}}}$
and
$C_{E, n, k}^{\operatorname {\mathrm {cyc}}}$
and
![]() $C_{E, n, k}^{\operatorname {\mathrm {prime}}}$
.
$C_{E, n, k}^{\operatorname {\mathrm {prime}}}$
.
Sections 4 and 5 are dedicated to the computation of the constants
![]() $C_{E, n, k}^{\mathcal {X}}$
for
$C_{E, n, k}^{\mathcal {X}}$
for
![]() $\mathcal {X} \in \{\operatorname {\mathrm {cyc}}, \operatorname {\mathrm {prime}}\}$
. These computations extend Zywina’s approach (a method that originates from Lang and Trotter’s work [Reference Lang and Trotter37] on the Lang–Trotter conjecture) to obtain
$\mathcal {X} \in \{\operatorname {\mathrm {cyc}}, \operatorname {\mathrm {prime}}\}$
. These computations extend Zywina’s approach (a method that originates from Lang and Trotter’s work [Reference Lang and Trotter37] on the Lang–Trotter conjecture) to obtain
![]() $C_{E}^{\operatorname {\mathrm {prime}}}$
. The general idea is to interpret the conditions for primes of Koblitz reduction for E in terms of mod m Galois representations, establish the heuristic constant at each level m, and then take the limit as
$C_{E}^{\operatorname {\mathrm {prime}}}$
. The general idea is to interpret the conditions for primes of Koblitz reduction for E in terms of mod m Galois representations, establish the heuristic constant at each level m, and then take the limit as
![]() $m\to \infty $
. In Section 4, we apply this idea to reformulate the constants
$m\to \infty $
. In Section 4, we apply this idea to reformulate the constants
![]() $C_E^{\operatorname {\mathrm {cyc}}}$
and
$C_E^{\operatorname {\mathrm {cyc}}}$
and
![]() $C_{E, n, k}^{\operatorname {\mathrm {cyc}}}$
and express
$C_{E, n, k}^{\operatorname {\mathrm {cyc}}}$
and express
![]() $C_{E, n, k}^{\operatorname {\mathrm {prime}}}$
in the form of an almost Euler product. We also propose the average constant
$C_{E, n, k}^{\operatorname {\mathrm {prime}}}$
in the form of an almost Euler product. We also propose the average constant
![]() $C_{n, k}^{\operatorname {\mathrm {prime}}}$
as a complete Euler product. In Section 5, we examine the special case where E is a Serre curve, proving Theorem 1.7 which gives explicit formulas for
$C_{n, k}^{\operatorname {\mathrm {prime}}}$
as a complete Euler product. In Section 5, we examine the special case where E is a Serre curve, proving Theorem 1.7 which gives explicit formulas for
![]() $C_{E, n, k}^{\operatorname {\mathrm {cyc}}}$
and
$C_{E, n, k}^{\operatorname {\mathrm {cyc}}}$
and
![]() $C_{E, n, k}^{\operatorname {\mathrm {prime}}}$
in this case. A critical aspect of these computations involves extracting as many Euler factors as possible from the limits (35) and (45), leading to the crucial definition of L in (7).
$C_{E, n, k}^{\operatorname {\mathrm {prime}}}$
in this case. A critical aspect of these computations involves extracting as many Euler factors as possible from the limits (35) and (45), leading to the crucial definition of L in (7).
Sections 6 and 7 establish bounds for moments of
![]() $C_{E, n, k}^{\operatorname {\mathrm {cyc}}}$
and
$C_{E, n, k}^{\operatorname {\mathrm {cyc}}}$
and
![]() $C_{E, n, k}^{\operatorname {\mathrm {prime}}}$
for
$C_{E, n, k}^{\operatorname {\mathrm {prime}}}$
for
![]() $E\in \mathcal {F}$
. In Section 6, we build on the work carried out in Section 5 to bound
$E\in \mathcal {F}$
. In Section 6, we build on the work carried out in Section 5 to bound
![]() $C^{\operatorname {\mathrm {prime}}}_{E,n,k}$
for non-Serre, non-CM curves, and CM curves. Using a result due to D. W. Masser and G. Wüstholz [Reference Masser and Wüstholz41], we bound
$C^{\operatorname {\mathrm {prime}}}_{E,n,k}$
for non-Serre, non-CM curves, and CM curves. Using a result due to D. W. Masser and G. Wüstholz [Reference Masser and Wüstholz41], we bound
![]() $C^{\operatorname {\mathrm {prime}}}_{E,n,k}$
for non-Serre, non-CM curves in terms of the naive height of E. This approach allows us to avoid assuming an affirmative answer to Serre’s uniformity question, in contrast to Jones. For CM elliptic curves, we first derive the conjectural constant
$C^{\operatorname {\mathrm {prime}}}_{E,n,k}$
for non-Serre, non-CM curves in terms of the naive height of E. This approach allows us to avoid assuming an affirmative answer to Serre’s uniformity question, in contrast to Jones. For CM elliptic curves, we first derive the conjectural constant
![]() $C_{E, n, k}^{\operatorname {\mathrm {prime}}}$
using a similar method to that of Sections 4 and 5 and bound it directly from its formula. In Section 7, we adapt the method of Jones [Reference Jones31] to complete the moments computations and prove Theorem 1.9.
$C_{E, n, k}^{\operatorname {\mathrm {prime}}}$
using a similar method to that of Sections 4 and 5 and bound it directly from its formula. In Section 7, we adapt the method of Jones [Reference Jones31] to complete the moments computations and prove Theorem 1.9.
Finally, in Section 8, we provide numerical examples that support our results. The numerical examples are computed using the Magma code available in this article’s GitHub repository [Reference Lee, Mayle and Wang39]:
https://github.com/maylejacobj/CyclicityKoblitzAPs.
We now summarize the main functions of the repository. The functions AvgCyclicityAP and AvgKoblitzAP allow one to compute
![]() $C^{\operatorname {\mathrm {cyc}}}_{n,k}$
and
$C^{\operatorname {\mathrm {cyc}}}_{n,k}$
and
![]() $C^{\operatorname {\mathrm {prime}}}_{n,k}$
for given coprime integers n and k, and were used to produce the tables above. Next, the functions CyclicityAP and KoblitzAP allow one to compute the constants
$C^{\operatorname {\mathrm {prime}}}_{n,k}$
for given coprime integers n and k, and were used to produce the tables above. Next, the functions CyclicityAP and KoblitzAP allow one to compute the constants
![]() $C_{E, n, k}^{\operatorname {\mathrm {cyc}}}$
and
$C_{E, n, k}^{\operatorname {\mathrm {cyc}}}$
and
![]() $C_{E, n, k}^{\operatorname {\mathrm {prime}}}$
for any given non-CM elliptic curve E. These functions are based on Propositions 4.10 and 4.4 and rely crucially on Zywina’s FindOpenImage function [Reference Zywina61] to compute the adelic image of E. The functions SerreCurveCyclicityAP and SerreCurveKoblitzAP compute
$C_{E, n, k}^{\operatorname {\mathrm {prime}}}$
for any given non-CM elliptic curve E. These functions are based on Propositions 4.10 and 4.4 and rely crucially on Zywina’s FindOpenImage function [Reference Zywina61] to compute the adelic image of E. The functions SerreCurveCyclicityAP and SerreCurveKoblitzAP compute
![]() $C_{E, n, k}^{\operatorname {\mathrm {cyc}}}$
and
$C_{E, n, k}^{\operatorname {\mathrm {cyc}}}$
and
![]() $C_{E, n, k}^{\operatorname {\mathrm {prime}}}$
for a given Serre curve E using Theorem 1.7 and do not require Zywina’s FindOpenImage. Lastly, the repository contains code for the examples in Section 8.
$C_{E, n, k}^{\operatorname {\mathrm {prime}}}$
for a given Serre curve E using Theorem 1.7 and do not require Zywina’s FindOpenImage. Lastly, the repository contains code for the examples in Section 8.
1.2 Notation and conventions
We now give a brief overview of the notation used throughout the article.
-
• For functions
 $f,g \colon \mathbb {R} \to \mathbb {R}$
, we write
$f,g \colon \mathbb {R} \to \mathbb {R}$
, we write
 $f \ll g$
or
$f \ll g$
or
 $f = \mathbf {O}(g)$
if there exists
$f = \mathbf {O}(g)$
if there exists
 $C> 0$
and
$C> 0$
and
 $x_0 \geq 0$
such that
$x_0 \geq 0$
such that
 $|f(x)| \leq Cg(x)$
for all
$|f(x)| \leq Cg(x)$
for all
 $x> x_0$
. If C depends on a parameter m, we write
$x> x_0$
. If C depends on a parameter m, we write
 $f \ll _m g$
or
$f \ll _m g$
or
 $f = \mathbf {O}_m(g)$
.
$f = \mathbf {O}_m(g)$
. -
• In the same setting as above, we write
 $f \sim g$
to denote that
$f \sim g$
to denote that
 $\lim _{x\to \infty } f(x)/g(x) = 1$
.
$\lim _{x\to \infty } f(x)/g(x) = 1$
. -
• Let A and B be positive real numbers. Let
 denote the family of models
denote the family of models
 $Y^2 = X^3 + aX+b$
of elliptic curves for which
$Y^2 = X^3 + aX+b$
of elliptic curves for which
 $|a| \leq A$
and
$|a| \leq A$
and
 $|b| \leq B$
.
$|b| \leq B$
. -
• Given a subfamily
 $\mathcal {G} \subseteq \mathcal {F}$
of elliptic curves, let f and g be functions defined from
$\mathcal {G} \subseteq \mathcal {F}$
of elliptic curves, let f and g be functions defined from
 $\mathcal {G}$
to
$\mathcal {G}$
to
 $\mathbb {R}$
. We write
$\mathbb {R}$
. We write
 $f \ll g$
if there exists an absolute constant
$f \ll g$
if there exists an absolute constant
 $M> 0$
for which
$M> 0$
for which
 $|f(E)| \leq Mg(E)$
for all
$|f(E)| \leq Mg(E)$
for all
 $E \in \mathcal {G}$
. When M depends on a parameter m, we write
$E \in \mathcal {G}$
. When M depends on a parameter m, we write
 $f \ll _m g$
.
$f \ll _m g$
. -
• p and
 $\ell $
denote rational primes, n a positive integer, and k an integer coprime to n.
$\ell $
denote rational primes, n a positive integer, and k an integer coprime to n. -
• We write
 $p^a \parallel n$
if
$p^a \parallel n$
if
 $p^a \mid n$
and
$p^a \mid n$
and
 $p^{a+1} \nmid n$
. In this case, a is called the p-adic valuation of n, and is denoted by
$p^{a+1} \nmid n$
. In this case, a is called the p-adic valuation of n, and is denoted by
 $v_p(n)$
.
$v_p(n)$
. -
• Given a positive integer n,
 $n^{\operatorname {\mathrm {odd}}}$
denotes the odd part of n, i.e.,
$n^{\operatorname {\mathrm {odd}}}$
denotes the odd part of n, i.e.,
 $n^{\operatorname {\mathrm {odd}}} = n/2^{v_2(n)}$
.
$n^{\operatorname {\mathrm {odd}}} = n/2^{v_2(n)}$
. -
• We sometimes write
 $(m,n)$
as shorthand for
$(m,n)$
as shorthand for
 $\gcd (m,n)$
.
$\gcd (m,n)$
. -
•
 $m^\infty $
denotes an arbitrarily large power of m. Thus,
$m^\infty $
denotes an arbitrarily large power of m. Thus,
 $\gcd (n,m^\infty )$
denotes
$\gcd (n,m^\infty )$
denotes
 $\prod _{p \mid (n,m)} p^{v_p(n)}$
. If every prime factor of n divides m, then we write
$\prod _{p \mid (n,m)} p^{v_p(n)}$
. If every prime factor of n divides m, then we write
 $n \mid m^\infty $
.
$n \mid m^\infty $
. -
•
 $\left (\frac {\cdot }{d}\right )$
denotes the Jacobi symbol.
$\left (\frac {\cdot }{d}\right )$
denotes the Jacobi symbol. -
•
 $\phi $
denotes the Euler totient function.
$\phi $
denotes the Euler totient function. -
•
 $\mu $
denotes the Möbius function.
$\mu $
denotes the Möbius function. -
•
 $G(m)$
denotes the image of a subgroup G of
$G(m)$
denotes the image of a subgroup G of
 $\operatorname {\mathrm {GL}}_2(\widehat {\mathbb {Z}})$
under the reduction modulo m map.
$\operatorname {\mathrm {GL}}_2(\widehat {\mathbb {Z}})$
under the reduction modulo m map. -
• Given that
 $d \mid m$
and
$d \mid m$
and
 $M \in \operatorname {\mathrm {GL}}_2(\mathbb {Z}/m\mathbb {Z})$
,
$M \in \operatorname {\mathrm {GL}}_2(\mathbb {Z}/m\mathbb {Z})$
,
 $M_d$
denotes the reduction of M modulo d.
$M_d$
denotes the reduction of M modulo d. -
• If
 $\mathcal {A}$
is the empty set, then we take
$\mathcal {A}$
is the empty set, then we take
 $\prod _{a\in \mathcal {A}} a$
to be
$\prod _{a\in \mathcal {A}} a$
to be
 $1$
.
$1$
.
2 Preliminaries
2.1 Galois representations and the adelic level
Let
![]() $E/\mathbb {Q}$
be an elliptic curve. Associated with E, we consider the adelic Tate module, which is given by the inverse limit
$E/\mathbb {Q}$
be an elliptic curve. Associated with E, we consider the adelic Tate module, which is given by the inverse limit
where
![]() $E[n]$
denotes the n-torsion subgroup of
$E[n]$
denotes the n-torsion subgroup of
![]() $E(\overline {\mathbb {Q}})$
. Let
$E(\overline {\mathbb {Q}})$
. Let
![]() $\widehat {\mathbb {Z}}$
denote the ring of profinite integers. It is well known that
$\widehat {\mathbb {Z}}$
denote the ring of profinite integers. It is well known that
![]() $T(E)$
is a free
$T(E)$
is a free
![]() $\widehat {\mathbb {Z}}$
-module of rank
$\widehat {\mathbb {Z}}$
-module of rank
![]() $2$
. The absolute Galois group
$2$
. The absolute Galois group
![]() $\operatorname {\mathrm {Gal}}(\overline {\mathbb {Q}}/\mathbb {Q})$
acts naturally on
$\operatorname {\mathrm {Gal}}(\overline {\mathbb {Q}}/\mathbb {Q})$
acts naturally on
![]() $T(E)$
, giving rise to the adelic Galois representation of E,
$T(E)$
, giving rise to the adelic Galois representation of E,
Upon fixing a
![]() $\widehat {\mathbb {Z}}$
-basis for
$\widehat {\mathbb {Z}}$
-basis for
![]() $T(E)$
, we consider
$T(E)$
, we consider
![]() $\rho _E$
as a map
$\rho _E$
as a map
Let
![]() $G_E$
denote the image of
$G_E$
denote the image of
![]() $\rho _E$
, which, because of the above choice of basis, is defined only up to conjugacy in
$\rho _E$
, which, because of the above choice of basis, is defined only up to conjugacy in
![]() $\operatorname {\mathrm {GL}}_2(\widehat {\mathbb {Z}})$
. With respect to the profinite topology on
$\operatorname {\mathrm {GL}}_2(\widehat {\mathbb {Z}})$
. With respect to the profinite topology on
![]() $\operatorname {\mathrm {GL}}_2(\widehat {\mathbb {Z}})$
, the subgroup
$\operatorname {\mathrm {GL}}_2(\widehat {\mathbb {Z}})$
, the subgroup
![]() $G_E$
is necessarily closed since
$G_E$
is necessarily closed since
![]() $\rho _E$
is a continuous map.
$\rho _E$
is a continuous map.
We now state a foundational result of Serre, known as Serre’s open image theorem.
Theorem 2.1 (Serre, [Reference Serre48, Théorème 3])
If
![]() $E/\mathbb {Q}$
is without complex multiplication, then
$E/\mathbb {Q}$
is without complex multiplication, then
![]() $G_E$
is an open subgroup of
$G_E$
is an open subgroup of
![]() $\operatorname {\mathrm {GL}}_2(\widehat {\mathbb {Z}})$
. In particular, the index
$\operatorname {\mathrm {GL}}_2(\widehat {\mathbb {Z}})$
. In particular, the index
![]() $[\operatorname {\mathrm {GL}}_2(\widehat {\mathbb {Z}}) : G_E]$
is finite.
$[\operatorname {\mathrm {GL}}_2(\widehat {\mathbb {Z}}) : G_E]$
is finite.
Suppose that
![]() $E/\mathbb {Q}$
is a non-CM elliptic curve. For each positive integer m, let
$E/\mathbb {Q}$
is a non-CM elliptic curve. For each positive integer m, let
![]() $\pi _m$
be the natural reduction map
$\pi _m$
be the natural reduction map
Let
![]() $G_E(m)$
be the image of the mod m Galois representation
$G_E(m)$
be the image of the mod m Galois representation
defined by the composition
![]() $\pi _m\circ \rho _E$
. It follows from Theorem 2.1 that there exists a positive integer m for which
$\pi _m\circ \rho _E$
. It follows from Theorem 2.1 that there exists a positive integer m for which
One may observe that (8) is equivalent to the statement that for every
![]() $n \in \mathbb {N}$
,
$n \in \mathbb {N}$
,
where
![]() $\pi \colon \operatorname {\mathrm {GL}}_2(\mathbb {Z}/n\mathbb {Z}) \to \operatorname {\mathrm {GL}}_2(\mathbb {Z}/\gcd (n,m)\mathbb {Z})$
denotes the natural reduction map. The least positive integer m with this property is called the adelic level of E, and is denoted by
$\pi \colon \operatorname {\mathrm {GL}}_2(\mathbb {Z}/n\mathbb {Z}) \to \operatorname {\mathrm {GL}}_2(\mathbb {Z}/\gcd (n,m)\mathbb {Z})$
denotes the natural reduction map. The least positive integer m with this property is called the adelic level of E, and is denoted by
![]() $m_E$
. The constant
$m_E$
. The constant
![]() $m_E$
accounts for both the nonsurjectivity of the
$m_E$
accounts for both the nonsurjectivity of the
![]() $\ell $
-adic Galois representations of E as well as the entanglements between their images.
$\ell $
-adic Galois representations of E as well as the entanglements between their images.
We now give a fundamental property of
![]() $m_E$
that we will use several times.
$m_E$
that we will use several times.
Lemma 2.2 Let
![]() $E/\mathbb {Q}$
be a non-CM elliptic curve of adelic level
$E/\mathbb {Q}$
be a non-CM elliptic curve of adelic level
![]() $m_E$
. For any
$m_E$
. For any
![]() $d_1,d_2 \in \mathbb {N}$
with
$d_1,d_2 \in \mathbb {N}$
with
![]() $d_1 \mid m_E^\infty $
and
$d_1 \mid m_E^\infty $
and
![]() $(d_2, m_E) = 1$
, we have
$(d_2, m_E) = 1$
, we have
via the map
![]() $\operatorname {\mathrm {GL}}_2(\mathbb {Z}/d_1d_2\mathbb {Z}) \to \operatorname {\mathrm {GL}}_2(\mathbb {Z}/d_1\mathbb {Z}) \times \operatorname {\mathrm {GL}}_2(\mathbb {Z}/d_2\mathbb {Z})$
.
$\operatorname {\mathrm {GL}}_2(\mathbb {Z}/d_1d_2\mathbb {Z}) \to \operatorname {\mathrm {GL}}_2(\mathbb {Z}/d_1\mathbb {Z}) \times \operatorname {\mathrm {GL}}_2(\mathbb {Z}/d_2\mathbb {Z})$
.
Proof By the given conditions, we have
![]() $(d_1,d_2) = 1$
. Set
$(d_1,d_2) = 1$
. Set
![]() $d^{\prime } = \gcd (d_1,m_E)$
. Let
$d^{\prime } = \gcd (d_1,m_E)$
. Let
![]() $\pi \colon \operatorname {\mathrm {GL}}_2(\mathbb {Z}/d_1d_2\mathbb {Z}) \to \operatorname {\mathrm {GL}}_2(\mathbb {Z}/d^{\prime }\mathbb {Z})$
and
$\pi \colon \operatorname {\mathrm {GL}}_2(\mathbb {Z}/d_1d_2\mathbb {Z}) \to \operatorname {\mathrm {GL}}_2(\mathbb {Z}/d^{\prime }\mathbb {Z})$
and
![]() $\pi _1 \colon \operatorname {\mathrm {GL}}_2(\mathbb {Z}/d_1\mathbb {Z}) \to \operatorname {\mathrm {GL}}_2(\mathbb {Z}/d^{\prime }\mathbb {Z})$
be the natural reduction maps. By the Chinese remainder theorem,
$\pi _1 \colon \operatorname {\mathrm {GL}}_2(\mathbb {Z}/d_1\mathbb {Z}) \to \operatorname {\mathrm {GL}}_2(\mathbb {Z}/d^{\prime }\mathbb {Z})$
be the natural reduction maps. By the Chinese remainder theorem,
![]() $\pi $
can be identified with
$\pi $
can be identified with
By (9), we have that
We conclude this subsection by recalling Serre’s uniformity question.
Question 2.3 Does there exist an absolute constant c such that for each elliptic curve
![]() $E/\mathbb {Q}$
,
$E/\mathbb {Q}$
,
holds for all rational primes
![]() $\ell> c$
?
$\ell> c$
?
While Question 2.3 remains open, it is widely conjectured to be true with
![]() $c = 37$
[Reference Sutherland56, Reference Zywina63] and considerable partial progress has been made toward its resolution [Reference Balakrishnan, Netan Dogra, Müller, Tuitman and Vonk4, Reference Furio and Lombardo25, Reference Lemos40, Reference Mazur43, Reference Serre48, Reference Serre49].
$c = 37$
[Reference Sutherland56, Reference Zywina63] and considerable partial progress has been made toward its resolution [Reference Balakrishnan, Netan Dogra, Müller, Tuitman and Vonk4, Reference Furio and Lombardo25, Reference Lemos40, Reference Mazur43, Reference Serre48, Reference Serre49].
2.2 Serre curves
In this subsection, we introduce the generic class of elliptic curves
![]() $E/\mathbb {Q}$
with maximal adelic Galois image
$E/\mathbb {Q}$
with maximal adelic Galois image
![]() $G_E$
, and provide an explicit description of
$G_E$
, and provide an explicit description of
![]() $G_E$
for curves in this class.
$G_E$
for curves in this class.
Serre noted [Reference Serre48] that for an elliptic curve
![]() $E/\mathbb {Q}$
, the adelic Galois representation
$E/\mathbb {Q}$
, the adelic Galois representation
![]() $\rho _E$
cannot be surjectiveFootnote
2
, that is, the adelic level
$\rho _E$
cannot be surjectiveFootnote
2
, that is, the adelic level
![]() $m_E$
is never
$m_E$
is never
![]() $1$
. We briefly give the argument here. If E has complex multiplication, then
$1$
. We briefly give the argument here. If E has complex multiplication, then
![]() $[\operatorname {\mathrm {GL}}_2(\widehat {\mathbb {Z}}):G_E]$
is necessarily infinite [Reference Serre48], so we restrict our attention to the case that E is non-CM. Assume that E is defined by the factored Weierstrass equation
$[\operatorname {\mathrm {GL}}_2(\widehat {\mathbb {Z}}):G_E]$
is necessarily infinite [Reference Serre48], so we restrict our attention to the case that E is non-CM. Assume that E is defined by the factored Weierstrass equation
with
![]() $e_1,e_2,e_3 \in \overline {\mathbb {Q}}$
. Then, the
$e_1,e_2,e_3 \in \overline {\mathbb {Q}}$
. Then, the
![]() $2$
-torsion of E is given by
$2$
-torsion of E is given by
Consequently,
![]() $\operatorname {\mathrm {Aut}}(E[2])$
can be identified with
$\operatorname {\mathrm {Aut}}(E[2])$
can be identified with
![]() $S_3$
. The discriminant
$S_3$
. The discriminant
![]() $\Delta _E$
of E is given by
$\Delta _E$
of E is given by
Let
![]() $\Delta '$
denote the squarefree part of
$\Delta '$
denote the squarefree part of
![]() $\Delta _E$
, i.e., the unique squarefree integer such that
$\Delta _E$
, i.e., the unique squarefree integer such that
![]() $\Delta _E/\Delta ^{\prime } \in (\mathbb {Q}^\times )^2$
. Note that the discriminant
$\Delta _E/\Delta ^{\prime } \in (\mathbb {Q}^\times )^2$
. Note that the discriminant
![]() $\Delta _E$
depends on the Weierstrass model of E, but
$\Delta _E$
depends on the Weierstrass model of E, but
![]() $\Delta ^{\prime }$
does not.
$\Delta ^{\prime }$
does not.
Let us first assume that
![]() $\Delta _E \not \in (\mathbb {Q}^\times )^2$
. Let
$\Delta _E \not \in (\mathbb {Q}^\times )^2$
. Let
![]() $d_E$
be the conductor of
$d_E$
be the conductor of
![]() $\mathbb {Q}(\sqrt {\Delta _E})$
, that is, the smallest positive integer such that
$\mathbb {Q}(\sqrt {\Delta _E})$
, that is, the smallest positive integer such that
![]() $\mathbb {Q}(\sqrt {\Delta _E}) \subseteq \mathbb {Q}(\zeta _{d_E})$
. It is straightforward to check that
$\mathbb {Q}(\sqrt {\Delta _E}) \subseteq \mathbb {Q}(\zeta _{d_E})$
. It is straightforward to check that
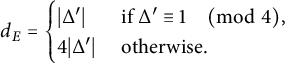 $$ \begin{align*}d_E = \begin{cases} |\Delta^{\prime}| & \text{ if } \Delta^{\prime} \equiv 1 \quad\pmod 4,\\ 4|\Delta^{\prime}| & \text{ otherwise}. \end{cases}\end{align*} $$
$$ \begin{align*}d_E = \begin{cases} |\Delta^{\prime}| & \text{ if } \Delta^{\prime} \equiv 1 \quad\pmod 4,\\ 4|\Delta^{\prime}| & \text{ otherwise}. \end{cases}\end{align*} $$
Let us define the quadratic character associated with
![]() $\mathbb {Q}(\sqrt {\Delta _E})$
as follows,
$\mathbb {Q}(\sqrt {\Delta _E})$
as follows,
Fix
![]() $\sigma \in \operatorname {\mathrm {Gal}}(\overline {\mathbb {Q}}/\mathbb {Q})$
. Viewing
$\sigma \in \operatorname {\mathrm {Gal}}(\overline {\mathbb {Q}}/\mathbb {Q})$
. Viewing
![]() $\rho _{E,2}(\sigma ) \in G_E(2) \subseteq \operatorname {\mathrm {Aut}}(E[2]) \simeq S_3$
, by (10), we notice that
$\rho _{E,2}(\sigma ) \in G_E(2) \subseteq \operatorname {\mathrm {Aut}}(E[2]) \simeq S_3$
, by (10), we notice that
where
![]() $\epsilon \colon S_3 \to \{\pm 1\}$
denotes the signature map.Footnote
3
Hence,
$\epsilon \colon S_3 \to \{\pm 1\}$
denotes the signature map.Footnote
3
Hence,
![]() $\chi _{\Delta _E}(\sigma ) = \epsilon (\rho _{E,2}(\sigma ))$
.
$\chi _{\Delta _E}(\sigma ) = \epsilon (\rho _{E,2}(\sigma ))$
.
On the other hand, we have that
![]() $\mathbb {Q}(\sqrt {\Delta _E}) \subseteq \mathbb {Q}(\zeta _{d_E})$
. Since
$\mathbb {Q}(\sqrt {\Delta _E}) \subseteq \mathbb {Q}(\zeta _{d_E})$
. Since
![]() $\operatorname {\mathrm {Gal}}(\mathbb {Q}(\zeta _{d_E})/\mathbb {Q}) \simeq (\mathbb {Z}/d_E\mathbb {Z})^\times $
, there exists a unique quadratic character
$\operatorname {\mathrm {Gal}}(\mathbb {Q}(\zeta _{d_E})/\mathbb {Q}) \simeq (\mathbb {Z}/d_E\mathbb {Z})^\times $
, there exists a unique quadratic character
![]() $\alpha \colon \operatorname {\mathrm {Gal}}(\mathbb {Q}(\zeta _{d_E})/\mathbb {Q}) \to \{\pm 1\}$
for which
$\alpha \colon \operatorname {\mathrm {Gal}}(\mathbb {Q}(\zeta _{d_E})/\mathbb {Q}) \to \{\pm 1\}$
for which
![]() $\chi _{\Delta _E}(\sigma ) = \alpha (\operatorname {det} \circ \rho _{E,{d_E}}(\sigma ))$
for any
$\chi _{\Delta _E}(\sigma ) = \alpha (\operatorname {det} \circ \rho _{E,{d_E}}(\sigma ))$
for any
![]() $\sigma \in \operatorname {\mathrm {Gal}}(\overline {\mathbb {Q}}/\mathbb {Q})$
. Therefore, we have
$\sigma \in \operatorname {\mathrm {Gal}}(\overline {\mathbb {Q}}/\mathbb {Q})$
. Therefore, we have
for any
![]() $\sigma \in \operatorname {\mathrm {Gal}}(\overline {\mathbb {Q}}/\mathbb {Q})$
.
$\sigma \in \operatorname {\mathrm {Gal}}(\overline {\mathbb {Q}}/\mathbb {Q})$
.
Let ![]() . Consider the subgroup
. Consider the subgroup
where
![]() $M_2$
and
$M_2$
and
![]() $M_{d_E}$
denote the reductions of M modulo
$M_{d_E}$
denote the reductions of M modulo
![]() $2$
and
$2$
and
![]() $d_E$
, respectively. Note that the index of
$d_E$
, respectively. Note that the index of
![]() $H_E(M_E)$
in
$H_E(M_E)$
in
![]() $\operatorname {\mathrm {GL}}_2(\mathbb {Z}/M_E\mathbb {Z})$
is
$\operatorname {\mathrm {GL}}_2(\mathbb {Z}/M_E\mathbb {Z})$
is
![]() $2$
and that
$2$
and that
![]() $G_E(M_E) \subseteq H_E(M_E)$
by (11). We define
$G_E(M_E) \subseteq H_E(M_E)$
by (11). We define
where
![]() $\pi \colon \operatorname {\mathrm {GL}}_2(\widehat {\mathbb {Z}}) \to \operatorname {\mathrm {GL}}_2(\mathbb {Z}/M_E\mathbb {Z})$
is the natural reduction map. Then
$\pi \colon \operatorname {\mathrm {GL}}_2(\widehat {\mathbb {Z}}) \to \operatorname {\mathrm {GL}}_2(\mathbb {Z}/M_E\mathbb {Z})$
is the natural reduction map. Then
![]() $H_E$
is an index
$H_E$
is an index
![]() $2$
subgroup of
$2$
subgroup of
![]() $\operatorname {\mathrm {GL}}_2(\widehat {\mathbb {Z}})$
that contains
$\operatorname {\mathrm {GL}}_2(\widehat {\mathbb {Z}})$
that contains
![]() $G_E$
. We say that E is a Serre curve if
$G_E$
. We say that E is a Serre curve if
![]() $H_E = G_E$
, that is,
$H_E = G_E$
, that is,
![]() $[\operatorname {\mathrm {GL}}_2(\widehat {\mathbb {Z}}):G_E] = 2$
.
$[\operatorname {\mathrm {GL}}_2(\widehat {\mathbb {Z}}):G_E] = 2$
.
In the above discussion, we supposed that
![]() $\Delta _E \not \in (\mathbb {Q}^\times )^2$
. We now consider the opposite case that
$\Delta _E \not \in (\mathbb {Q}^\times )^2$
. We now consider the opposite case that
![]() $\Delta _E \in (\mathbb {Q}^\times )^2$
. Let
$\Delta _E \in (\mathbb {Q}^\times )^2$
. Let
![]() $\mathbb {Q}(E[2]) = \mathbb {Q}(e_1,e_2,e_3)$
denote the
$\mathbb {Q}(E[2]) = \mathbb {Q}(e_1,e_2,e_3)$
denote the
![]() $2$
-division field of E. Observe that
$2$
-division field of E. Observe that
![]() $[\mathbb {Q}(E[2]):\mathbb {Q}]$
divides
$[\mathbb {Q}(E[2]):\mathbb {Q}]$
divides
![]() $3$
, and hence
$3$
, and hence
![]() $[\operatorname {\mathrm {GL}}_2(\mathbb {Z}/2\mathbb {Z}) : G_E(2)]$
is divisible by
$[\operatorname {\mathrm {GL}}_2(\mathbb {Z}/2\mathbb {Z}) : G_E(2)]$
is divisible by
![]() $2$
. Thus, by [Reference Mayle and Rakvi42, Proposition 2.14],
$2$
. Thus, by [Reference Mayle and Rakvi42, Proposition 2.14],
![]() $[\operatorname {\mathrm {GL}}_2(\widehat {\mathbb {Z}}) : G_E] \geq 12$
, which follows by considering the index of the commutator of
$[\operatorname {\mathrm {GL}}_2(\widehat {\mathbb {Z}}) : G_E] \geq 12$
, which follows by considering the index of the commutator of
![]() $G_E$
in
$G_E$
in
![]() $\operatorname {\mathrm {SL}}_2(\widehat {\mathbb {Z}})$
. In particular, E cannot be a Serre curve in this case.
$\operatorname {\mathrm {SL}}_2(\widehat {\mathbb {Z}})$
. In particular, E cannot be a Serre curve in this case.
Serre curves are useful for us for two key reasons. First, as mentioned in the introduction, Jones [Reference Jones32] showed that they are “generic” in the sense that the density of the subfamily of Serre curves among the family of all elliptic curves ordered by naive height is
![]() $1$
. Second, the adelic image
$1$
. Second, the adelic image
![]() $G_E$
of a Serre curve E can be explicitly described, as we will now discuss.
$G_E$
of a Serre curve E can be explicitly described, as we will now discuss.
Proposition 2.4 Let
![]() $E/\mathbb {Q}$
be a Serre curve and write
$E/\mathbb {Q}$
be a Serre curve and write
![]() $\Delta ^{\prime }$
to denote the squarefree part of the discriminant of E. Then
$\Delta ^{\prime }$
to denote the squarefree part of the discriminant of E. Then
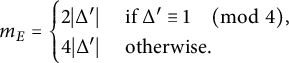 $$ \begin{align} m_E = \begin{cases} 2|\Delta^{\prime}| & \text{ if } \Delta^{\prime} \equiv 1 \quad\pmod 4,\\ 4|\Delta^{\prime}| & \text{ otherwise}. \end{cases} \end{align} $$
$$ \begin{align} m_E = \begin{cases} 2|\Delta^{\prime}| & \text{ if } \Delta^{\prime} \equiv 1 \quad\pmod 4,\\ 4|\Delta^{\prime}| & \text{ otherwise}. \end{cases} \end{align} $$
Furthermore, for any positive integer m,
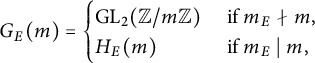 $$ \begin{align*}G_E(m) = \begin{cases} \operatorname{\mathrm{GL}}_2(\mathbb{Z}/m\mathbb{Z}) & \text{ if } m_E \nmid m, \\ H_E(m) & \text{ if } m_E \mid m, \end{cases}\end{align*} $$
$$ \begin{align*}G_E(m) = \begin{cases} \operatorname{\mathrm{GL}}_2(\mathbb{Z}/m\mathbb{Z}) & \text{ if } m_E \nmid m, \\ H_E(m) & \text{ if } m_E \mid m, \end{cases}\end{align*} $$
where
![]() $H_E(m)$
denotes the image of
$H_E(m)$
denotes the image of
![]() $H_E$
, defined in (12), under the reduction modulo m map.
$H_E$
, defined in (12), under the reduction modulo m map.
Proof The proof of (13) can be found in [Reference Jones31, pp. 696–697]. Hence,
![]() $m_E = M_E$
where
$m_E = M_E$
where
![]() $M_E$
is defined as above. Now, let m be a positive integer. By [Reference Jones31, Equation (13)] and (9), one may deduce that
$M_E$
is defined as above. Now, let m be a positive integer. By [Reference Jones31, Equation (13)] and (9), one may deduce that
![]() $G_E(m) = \operatorname {\mathrm {GL}}_2(\mathbb {Z}/m\mathbb {Z})$
if
$G_E(m) = \operatorname {\mathrm {GL}}_2(\mathbb {Z}/m\mathbb {Z})$
if
![]() $m_E \nmid m$
. Suppose
$m_E \nmid m$
. Suppose
![]() $m_E \mid m$
. Then,
$m_E \mid m$
. Then,
![]() $G_E(m) \subseteq H_E(m)$
. The containment must be equal; otherwise, the index of
$G_E(m) \subseteq H_E(m)$
. The containment must be equal; otherwise, the index of
![]() $G_E$
in
$G_E$
in
![]() $\operatorname {\mathrm {GL}}_2(\widehat {\mathbb {Z}})$
is greater than
$\operatorname {\mathrm {GL}}_2(\widehat {\mathbb {Z}})$
is greater than
![]() $[\operatorname {\mathrm {GL}}_2(\mathbb {Z}/m\mathbb {Z}) : H_E(m)] = [\operatorname {\mathrm {GL}}_2(\mathbb {Z}/m_E\mathbb {Z}) : H_E(m_E)] = 2$
, contradicting the assumption that
$[\operatorname {\mathrm {GL}}_2(\mathbb {Z}/m\mathbb {Z}) : H_E(m)] = [\operatorname {\mathrm {GL}}_2(\mathbb {Z}/m_E\mathbb {Z}) : H_E(m_E)] = 2$
, contradicting the assumption that
![]() $E/\mathbb {Q}$
is a Serre curve.
$E/\mathbb {Q}$
is a Serre curve.
In order to compute
![]() $C^{\mathcal {X}}_{E,n,k}$
, we need to know
$C^{\mathcal {X}}_{E,n,k}$
, we need to know
![]() $G_E$
(meaning we must know the adelic level
$G_E$
(meaning we must know the adelic level
![]() $m_E$
and the image of
$m_E$
and the image of
![]() $G_E$
modulo
$G_E$
modulo
![]() $m_E$
). For Serre curves, this is particularly tractable, and was exploited in the work of Jones [Reference Jones31]. We now give the description of
$m_E$
). For Serre curves, this is particularly tractable, and was exploited in the work of Jones [Reference Jones31]. We now give the description of
![]() $G_E$
for Serre curves.
$G_E$
for Serre curves.
First, we define
![]() $\chi _4 \colon (\mathbb {Z}/4\mathbb {Z})^\times \to \{\pm 1\}$
and
$\chi _4 \colon (\mathbb {Z}/4\mathbb {Z})^\times \to \{\pm 1\}$
and
![]() $\chi _8 \colon (\mathbb {Z}/8\mathbb {Z})^\times \to \{\pm 1\}$
as follows:
$\chi _8 \colon (\mathbb {Z}/8\mathbb {Z})^\times \to \{\pm 1\}$
as follows:
 $$\begin{align*}\chi_4(k) = \begin{cases} 1 & \text{ if }k\equiv 1\quad\pmod 4\\ -1 & \text{ if }k\equiv 3\quad\pmod 4 \end{cases}, \quad \chi_8(k)=\begin{cases} 1 & \text{ if }k\equiv 1, 7\quad\pmod 8\\ -1 & \text{ if }k\equiv 3, 5\quad\pmod 8 \end{cases}. \end{align*}$$
$$\begin{align*}\chi_4(k) = \begin{cases} 1 & \text{ if }k\equiv 1\quad\pmod 4\\ -1 & \text{ if }k\equiv 3\quad\pmod 4 \end{cases}, \quad \chi_8(k)=\begin{cases} 1 & \text{ if }k\equiv 1, 7\quad\pmod 8\\ -1 & \text{ if }k\equiv 3, 5\quad\pmod 8 \end{cases}. \end{align*}$$
We define the character
![]() $\psi _m \colon \operatorname {\mathrm {GL}}_2(\mathbb {Z}/m\mathbb {Z}) \to \{\pm 1\}$
associated with E by
$\psi _m \colon \operatorname {\mathrm {GL}}_2(\mathbb {Z}/m\mathbb {Z}) \to \{\pm 1\}$
associated with E by
where
![]() $\psi _{\ell ^\alpha } \colon \operatorname {\mathrm {GL}}_2(\mathbb {Z}/\ell ^\alpha \mathbb {Z}) \to \{\pm 1\}$
is defined for
$\psi _{\ell ^\alpha } \colon \operatorname {\mathrm {GL}}_2(\mathbb {Z}/\ell ^\alpha \mathbb {Z}) \to \{\pm 1\}$
is defined for
![]() $M \in \operatorname {\mathrm {GL}}_2(\mathbb {Z}/\ell ^\alpha \mathbb {Z})$
by
$M \in \operatorname {\mathrm {GL}}_2(\mathbb {Z}/\ell ^\alpha \mathbb {Z})$
by
 $$ \begin{align*} \psi_{\ell^\alpha}(M) = \begin{cases} \left( \frac{\operatorname{det} M_\ell}{\ell}\right) & \text{ if } \ell \text{ is odd},\\ \epsilon(M_2) & \text{ if } \ell= 2, \alpha \geq 1, \text{ and } \Delta^{\prime} \equiv 1 \quad\pmod 4, \\ \chi_4(\operatorname{det} M_4) \epsilon(M_2) & \text{ if } \ell = 2 , \alpha \geq 2,\text{ and } \Delta^{\prime} \equiv 3 \quad\pmod 4, \\ \chi_8(\operatorname{det} M_8) \epsilon(M_2) & \text{ if } \ell =2 , \alpha \geq 3,\text{ and } \Delta^{\prime} \equiv 2 \quad\pmod 8,\\ \chi_8(\operatorname{det} M_8) \chi_4(\operatorname{det} M_4) \epsilon(M_2) & \text{ if } \ell = 2 , \alpha \geq 3, \text{ and } \Delta^{\prime} \equiv 6 \quad\pmod 8, \\ 1 & \text{ otherwise}. \end{cases} \end{align*} $$
$$ \begin{align*} \psi_{\ell^\alpha}(M) = \begin{cases} \left( \frac{\operatorname{det} M_\ell}{\ell}\right) & \text{ if } \ell \text{ is odd},\\ \epsilon(M_2) & \text{ if } \ell= 2, \alpha \geq 1, \text{ and } \Delta^{\prime} \equiv 1 \quad\pmod 4, \\ \chi_4(\operatorname{det} M_4) \epsilon(M_2) & \text{ if } \ell = 2 , \alpha \geq 2,\text{ and } \Delta^{\prime} \equiv 3 \quad\pmod 4, \\ \chi_8(\operatorname{det} M_8) \epsilon(M_2) & \text{ if } \ell =2 , \alpha \geq 3,\text{ and } \Delta^{\prime} \equiv 2 \quad\pmod 8,\\ \chi_8(\operatorname{det} M_8) \chi_4(\operatorname{det} M_4) \epsilon(M_2) & \text{ if } \ell = 2 , \alpha \geq 3, \text{ and } \Delta^{\prime} \equiv 6 \quad\pmod 8, \\ 1 & \text{ otherwise}. \end{cases} \end{align*} $$
As noted in [Reference Jones31, p. 701], given
![]() $m_E\mid m$
, one may see that for
$m_E\mid m$
, one may see that for
![]() $M \in \operatorname {\mathrm {GL}}_2(\mathbb {Z}/m\mathbb {Z})$
, we have
$M \in \operatorname {\mathrm {GL}}_2(\mathbb {Z}/m\mathbb {Z})$
, we have
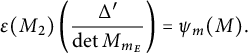 $$ \begin{align*}\epsilon(M_2) \left(\frac{\Delta^{\prime}}{\operatorname{det} M_{m_E}}\right) = \psi_m(M).\end{align*} $$
$$ \begin{align*}\epsilon(M_2) \left(\frac{\Delta^{\prime}}{\operatorname{det} M_{m_E}}\right) = \psi_m(M).\end{align*} $$
In particular, we have
![]() $H_E(m) = \ker \psi _m$
. Thus
$H_E(m) = \ker \psi _m$
. Thus
![]() $G_E$
is the preimage of
$G_E$
is the preimage of
![]() $\ker \psi _m$
in
$\ker \psi _m$
in
![]() $\operatorname {\mathrm {GL}}_2(\widehat {\mathbb {Z}})$
.
$\operatorname {\mathrm {GL}}_2(\widehat {\mathbb {Z}})$
.
2.3 Galois representations in the CM case
Having discussed Galois representations for non-CM elliptic curves, we now turn to the CM case. Suppose that E has CM by an order
![]() $\mathcal {O}$
in an imaginary quadratic field K. In this case, the absolute Galois group
$\mathcal {O}$
in an imaginary quadratic field K. In this case, the absolute Galois group
![]() $\operatorname {\mathrm {Gal}}(\overline {K}/K)$
acts naturally on
$\operatorname {\mathrm {Gal}}(\overline {K}/K)$
acts naturally on
![]() $T(E)$
, which is a one-dimensional
$T(E)$
, which is a one-dimensional
![]() $\widehat {\mathcal {O}}$
-module, where
$\widehat {\mathcal {O}}$
-module, where
![]() $\widehat {\mathcal {O}}$
denotes the profinite completion of
$\widehat {\mathcal {O}}$
denotes the profinite completion of
![]() $\mathcal {O}$
. Hence, we can construct the adelic Galois representation associated with E,
$\mathcal {O}$
. Hence, we can construct the adelic Galois representation associated with E,
Let
![]() $G_E$
denote the image of
$G_E$
denote the image of
![]() $\rho _E$
. We now state Serre’s open image theorem for CM elliptic curves.
$\rho _E$
. We now state Serre’s open image theorem for CM elliptic curves.
Theorem 2.5 (Serre, [Reference Serre48, p. 302, Corollaire])
If
![]() $E/\mathbb {Q}$
has CM by
$E/\mathbb {Q}$
has CM by
![]() $\mathcal {O}$
, then
$\mathcal {O}$
, then
![]() $G_E$
is an open subgroup of
$G_E$
is an open subgroup of
![]() $\widehat {\mathcal {O}}^\times $
. In particular, the index
$\widehat {\mathcal {O}}^\times $
. In particular, the index
![]() $[\widehat {\mathcal {O}}^\times : G_E]$
is finite.
$[\widehat {\mathcal {O}}^\times : G_E]$
is finite.
For each positive integer m, consider the natural reduction map
Let
![]() $G_E(m)$
denote the image of the modulo m Galois representation
$G_E(m)$
denote the image of the modulo m Galois representation
defined by the composition
![]() $\pi _m\circ \rho _E$
. It follows from Theorem 2.5 that
$\pi _m\circ \rho _E$
. It follows from Theorem 2.5 that
for some positive integer m. As in the non-CM case, (14) is equivalent to the statement that for every
![]() $n \in \mathbb {N}$
,
$n \in \mathbb {N}$
,
where
![]() $\pi \colon (\mathcal {O}/n\mathcal {O})^{\times }\to (\mathcal {O}/\gcd (n, m)\mathcal {O})^{\times }$
is the natural reduction map.
$\pi \colon (\mathcal {O}/n\mathcal {O})^{\times }\to (\mathcal {O}/\gcd (n, m)\mathcal {O})^{\times }$
is the natural reduction map.
In the CM case, we follow [Reference Jones31, p. 693] to define
![]() $m_E$
to be the smallest positive integer m such that (15) holds and for which
$m_E$
to be the smallest positive integer m such that (15) holds and for which
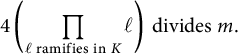 $$ \begin{align} 4 \left( \prod_{\ell \text{ ramifies in }K} \ell \right) \text{ divides } m. \end{align} $$
$$ \begin{align} 4 \left( \prod_{\ell \text{ ramifies in }K} \ell \right) \text{ divides } m. \end{align} $$
One can prove the following using the same argument sketched in the proof of Lemma 2.2.
Lemma 2.6 Let
![]() $E/\mathbb {Q}$
be a CM elliptic curve of level
$E/\mathbb {Q}$
be a CM elliptic curve of level
![]() $m_E$
. For any
$m_E$
. For any
![]() $d_1,d_2 \in \mathbb {N}$
with
$d_1,d_2 \in \mathbb {N}$
with
![]() $d_1 \mid m_E^\infty $
and
$d_1 \mid m_E^\infty $
and
![]() $(d_2, m_E) = 1$
, we have
$(d_2, m_E) = 1$
, we have
Lemmas 2.2 and 2.6 are used to express the constants
![]() $C^{\operatorname {\mathrm {cyc}}}_{E,n,k}$
and
$C^{\operatorname {\mathrm {cyc}}}_{E,n,k}$
and
![]() $C^{\operatorname {\mathrm {prime}}}_{E,n,k}$
as almost Euler products. It is worth noting that both lemmas hold even if
$C^{\operatorname {\mathrm {prime}}}_{E,n,k}$
as almost Euler products. It is worth noting that both lemmas hold even if
![]() $m_E$
is replaced by any positive multiple of it. Thus, the minimality condition in the definition of
$m_E$
is replaced by any positive multiple of it. Thus, the minimality condition in the definition of
![]() $m_E$
for both non-CM and CM curves is not required from a theoretical perspective for us. Nonetheless, the minimality of
$m_E$
for both non-CM and CM curves is not required from a theoretical perspective for us. Nonetheless, the minimality of
![]() $m_E$
is useful for our computations as it allows us to extract more Euler factors.
$m_E$
is useful for our computations as it allows us to extract more Euler factors.
Let
![]() $K/\mathbb {Q}$
be an imaginary quadratic field. We denote its ring of integers by
$K/\mathbb {Q}$
be an imaginary quadratic field. We denote its ring of integers by
![]() $\mathcal {O}_K$
. Let
$\mathcal {O}_K$
. Let
![]() $\mathcal {O}$
be an order of K. The index
$\mathcal {O}$
be an order of K. The index
![]() $f = [\mathcal {O}_K : \mathcal {O}]$
is necessarily finite and is called the conductor of
$f = [\mathcal {O}_K : \mathcal {O}]$
is necessarily finite and is called the conductor of
![]() $\mathcal {O}$
. Let
$\mathcal {O}$
. Let
![]() $\chi _K$
be the Dirichlet character defined by
$\chi _K$
be the Dirichlet character defined by
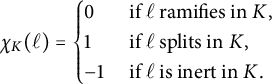 $$ \begin{align} \chi_K(\ell) =\begin{cases} 0 & \text{ if } \ell \text{ ramifies in } K, \\ 1 & \text{ if } \ell \text{ splits in } K, \\ -1 & \text{ if } \ell \text{ is inert in } K. \end{cases} \end{align} $$
$$ \begin{align} \chi_K(\ell) =\begin{cases} 0 & \text{ if } \ell \text{ ramifies in } K, \\ 1 & \text{ if } \ell \text{ splits in } K, \\ -1 & \text{ if } \ell \text{ is inert in } K. \end{cases} \end{align} $$
Let
![]() $d_K$
be the discriminant of K. One can check that
$d_K$
be the discriminant of K. One can check that
for each odd prime
![]() $\ell $
. By [Reference Montgomery and Vaughan45, Theorem 9.13], we see that
$\ell $
. By [Reference Montgomery and Vaughan45, Theorem 9.13], we see that
![]() $\chi _K$
is a primitive quadratic character.
$\chi _K$
is a primitive quadratic character.
We now state a lemma on the size of the image of mod
![]() $\ell ^\alpha $
Galois representation of E for
$\ell ^\alpha $
Galois representation of E for
![]() $\ell \nmid fm_E$
.
$\ell \nmid fm_E$
.
Lemma 2.7 Let
![]() $E/\mathbb {Q}$
be a CM elliptic curve. For
$E/\mathbb {Q}$
be a CM elliptic curve. For
![]() $\ell \nmid fm_E$
, we have
$\ell \nmid fm_E$
, we have
Proof Since
![]() $\mathcal {O}$
is an order of class number
$\mathcal {O}$
is an order of class number
![]() $1$
, we have
$1$
, we have
for any
![]() $\ell \nmid f$
. (See [Reference Cox21, Proposition 7.20].) By Lemma 2.6, we have
$\ell \nmid f$
. (See [Reference Cox21, Proposition 7.20].) By Lemma 2.6, we have
![]() $G_E(\ell ^\alpha ) \simeq \left (\mathcal {O}_K/\ell ^\alpha \mathcal {O}_K\right )^\times $
. Applying [Reference Bröker, Lauter and Sutherland13, Equation (4)], we obtain the desired results.
$G_E(\ell ^\alpha ) \simeq \left (\mathcal {O}_K/\ell ^\alpha \mathcal {O}_K\right )^\times $
. Applying [Reference Bröker, Lauter and Sutherland13, Equation (4)], we obtain the desired results.
Moreover, we have the following uniformity result for CM elliptic curves over
![]() $\mathbb {Q}$
.
$\mathbb {Q}$
.
Proposition 2.8 There is an absolute constant C such that
holds for all CM elliptic curves
![]() $E / \mathbb {Q}$
.
$E / \mathbb {Q}$
.
Proof It suffices to show that the index
![]() $[\widehat {\mathcal {O}}^\times : G_E]$
, the product of ramified primes in (16), and the conductor
$[\widehat {\mathcal {O}}^\times : G_E]$
, the product of ramified primes in (16), and the conductor
![]() $f = [\mathcal {O}_K : \mathcal {O}]$
of the CM-order
$f = [\mathcal {O}_K : \mathcal {O}]$
of the CM-order
![]() $\mathcal {O}$
are uniformly bounded for
$\mathcal {O}$
are uniformly bounded for
![]() $E/\mathbb {Q}$
. This follows from the fact that there are only finitely many endomorphism rings for CM elliptic curves over
$E/\mathbb {Q}$
. This follows from the fact that there are only finitely many endomorphism rings for CM elliptic curves over
![]() $\mathbb {Q}$
and [Reference Bourdon and Clark11, Theorem 1.1]. In fact, for CM elliptic curves
$\mathbb {Q}$
and [Reference Bourdon and Clark11, Theorem 1.1]. In fact, for CM elliptic curves
![]() $E/\mathbb {Q}$
, it is known that the conductor of
$E/\mathbb {Q}$
, it is known that the conductor of
![]() $\mathcal {O}$
is at most
$\mathcal {O}$
is at most
![]() $3$
. (See [Reference Silverman52, Appendix C, Example 11.3.2].)
$3$
. (See [Reference Silverman52, Appendix C, Example 11.3.2].)
3 Counting matrices
In this section, we will establish counting results that will play pivotal roles in determining the cyclicity and Koblitz constants for arithmetic progressions. We first outline the general strategy.
Let
![]() $\ell $
be a prime and
$\ell $
be a prime and
![]() $\mathcal {P}_\ell $
be a property that certain matrices in
$\mathcal {P}_\ell $
be a property that certain matrices in
![]() $\operatorname {\mathrm {GL}}_2(\mathbb {Z}/\ell \mathbb {Z})$
satisfy. Let m and n be positive integers and k be coprime to n. Suppose that we are interested in counting the size of the set
$\operatorname {\mathrm {GL}}_2(\mathbb {Z}/\ell \mathbb {Z})$
satisfy. Let m and n be positive integers and k be coprime to n. Suppose that we are interested in counting the size of the set
where
![]() $M_\ell $
denotes the reduction of M modulo
$M_\ell $
denotes the reduction of M modulo
![]() $\ell $
. By the Chinese remainder theorem, it suffices to count the size of
$\ell $
. By the Chinese remainder theorem, it suffices to count the size of
![]() $X(\ell ^a)$
for each
$X(\ell ^a)$
for each
![]() $\ell ^a \parallel m$
. Also, note that the reduction map
$\ell ^a \parallel m$
. Also, note that the reduction map
![]() $\pi : \operatorname {\mathrm {GL}}_2(\mathbb {Z}/\ell ^a\mathbb {Z}) \to \operatorname {\mathrm {GL}}_2(\mathbb {Z}/\ell \mathbb {Z})$
induces a surjective map
$\pi : \operatorname {\mathrm {GL}}_2(\mathbb {Z}/\ell ^a\mathbb {Z}) \to \operatorname {\mathrm {GL}}_2(\mathbb {Z}/\ell \mathbb {Z})$
induces a surjective map
![]() $X(\ell ^a) \to X(\ell )$
and further
$X(\ell ^a) \to X(\ell )$
and further
![]() $X(\ell ^a) = \pi ^{-1}( X(\ell ))$
. Consequently, the problem of counting the size of
$X(\ell ^a) = \pi ^{-1}( X(\ell ))$
. Consequently, the problem of counting the size of
![]() $X(m)$
reduces to counting the size of
$X(m)$
reduces to counting the size of
![]() $X(\ell )$
for each
$X(\ell )$
for each
![]() $\ell \mid m$
.
$\ell \mid m$
.
The condition that
![]() $\ell $
is a prime of cyclic or Koblitz reduction for E can be interpreted as a condition on matrices modulo primes. Thus, with the above strategy in mind, we give a lemma and corollary that will be used to compute the cyclicity constant
$\ell $
is a prime of cyclic or Koblitz reduction for E can be interpreted as a condition on matrices modulo primes. Thus, with the above strategy in mind, we give a lemma and corollary that will be used to compute the cyclicity constant
![]() $C^{\operatorname {\mathrm {cyc}}}_{E,n,k}$
for non-CM curves.
$C^{\operatorname {\mathrm {cyc}}}_{E,n,k}$
for non-CM curves.
Lemma 3.1 Let
![]() $\ell $
be a prime, a be a positive integer, and k be an integer coprime to
$\ell $
be a prime, a be a positive integer, and k be an integer coprime to
![]() $\ell $
. Fix
$\ell $
. Fix
![]() $M \in \operatorname {\mathrm {GL}}_2(\mathbb {Z}/\ell \mathbb {Z})$
with
$M \in \operatorname {\mathrm {GL}}_2(\mathbb {Z}/\ell \mathbb {Z})$
with
![]() $\operatorname {det} M \equiv k \ \pmod \ell $
. For any integer
$\operatorname {det} M \equiv k \ \pmod \ell $
. For any integer
![]() $\widetilde {k}$
with
$\widetilde {k}$
with
![]() $\widetilde {k} \equiv k \ \pmod \ell $
, we have
$\widetilde {k} \equiv k \ \pmod \ell $
, we have
Proof Let
![]() $\pi \colon \operatorname {\mathrm {GL}}_2(\mathbb {Z}/\ell ^a\mathbb {Z}) \to \operatorname {\mathrm {GL}}_2(\mathbb {Z}/\ell \mathbb {Z})$
denote the reduction modulo
$\pi \colon \operatorname {\mathrm {GL}}_2(\mathbb {Z}/\ell ^a\mathbb {Z}) \to \operatorname {\mathrm {GL}}_2(\mathbb {Z}/\ell \mathbb {Z})$
denote the reduction modulo
![]() $\ell $
map, which is a surjective group homomorphism. For any
$\ell $
map, which is a surjective group homomorphism. For any
![]() $M\in \operatorname {\mathrm {GL}}_2(\mathbb {Z}/\ell \mathbb {Z})$
, we have that
$M\in \operatorname {\mathrm {GL}}_2(\mathbb {Z}/\ell \mathbb {Z})$
, we have that
The image of
![]() $\pi ^{-1}(M)$
under
$\pi ^{-1}(M)$
under
![]() $\operatorname {det} \colon \operatorname {\mathrm {GL}}_2(\mathbb {Z}/\ell ^a\mathbb {Z}) \to (\mathbb {Z}/\ell ^a\mathbb {Z})^\times $
is
$\operatorname {det} \colon \operatorname {\mathrm {GL}}_2(\mathbb {Z}/\ell ^a\mathbb {Z}) \to (\mathbb {Z}/\ell ^a\mathbb {Z})^\times $
is
Hence, for any integer
![]() $\widetilde {k}$
with
$\widetilde {k}$
with
![]() $\widetilde {k} \equiv k \ \pmod \ell $
, we have
$\widetilde {k} \equiv k \ \pmod \ell $
, we have
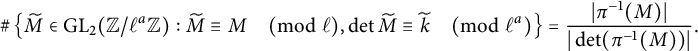 $$ \begin{align*} \#\left\{\widetilde{M} \in \operatorname{\mathrm{GL}}_2(\mathbb{Z}/\ell^a\mathbb{Z}) : \widetilde{M} \equiv M \quad\pmod \ell, \operatorname{det} \widetilde{M} \equiv \widetilde{k} \quad\pmod {\ell^a} \right\} &= \frac{| \pi^{-1}(M) |}{| \operatorname{det}(\pi^{-1}(M)) |}. \end{align*} $$
$$ \begin{align*} \#\left\{\widetilde{M} \in \operatorname{\mathrm{GL}}_2(\mathbb{Z}/\ell^a\mathbb{Z}) : \widetilde{M} \equiv M \quad\pmod \ell, \operatorname{det} \widetilde{M} \equiv \widetilde{k} \quad\pmod {\ell^a} \right\} &= \frac{| \pi^{-1}(M) |}{| \operatorname{det}(\pi^{-1}(M)) |}. \end{align*} $$
Finally, we note that
![]() $| \pi ^{-1}(M) | = | \ker (\pi ) | = \ell ^{4(a-1)}$
and
$| \pi ^{-1}(M) | = | \ker (\pi ) | = \ell ^{4(a-1)}$
and
![]() $| \operatorname {det}(\pi ^{-1}(M)) | = \ell ^{a-1}$
.
$| \operatorname {det}(\pi ^{-1}(M)) | = \ell ^{a-1}$
.
Corollary 3.2 Fix a prime
![]() $\ell $
and positive integer a. Let k be an integer coprime to
$\ell $
and positive integer a. Let k be an integer coprime to
![]() $\ell $
. Then
$\ell $
. Then
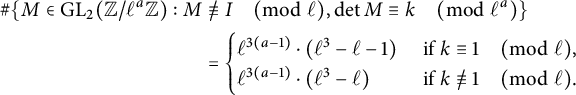 $$ \begin{align*} \#\{M \in \operatorname{\mathrm{GL}}_2(\mathbb{Z}/\ell^a\mathbb{Z}) : M &\not \equiv I \quad\pmod \ell, \operatorname{det} M \equiv k \quad\pmod {\ell^a} \} \\ &= \begin{cases} \ell^{3(a-1)} \cdot (\ell^3-\ell-1) & \text{ if } k \equiv 1 \quad\pmod \ell, \\ \ell^{3(a-1)} \cdot (\ell^3-\ell) & \text{ if } k \not \equiv 1 \quad\pmod \ell. \end{cases} \end{align*} $$
$$ \begin{align*} \#\{M \in \operatorname{\mathrm{GL}}_2(\mathbb{Z}/\ell^a\mathbb{Z}) : M &\not \equiv I \quad\pmod \ell, \operatorname{det} M \equiv k \quad\pmod {\ell^a} \} \\ &= \begin{cases} \ell^{3(a-1)} \cdot (\ell^3-\ell-1) & \text{ if } k \equiv 1 \quad\pmod \ell, \\ \ell^{3(a-1)} \cdot (\ell^3-\ell) & \text{ if } k \not \equiv 1 \quad\pmod \ell. \end{cases} \end{align*} $$
Proof Let
![]() $M \in \operatorname {\mathrm {GL}}_2(\mathbb {Z}/\ell \mathbb {Z})$
. If
$M \in \operatorname {\mathrm {GL}}_2(\mathbb {Z}/\ell \mathbb {Z})$
. If
![]() $M \not \equiv I \ \pmod {\ell }$
, then any lifting
$M \not \equiv I \ \pmod {\ell }$
, then any lifting
![]() $\widetilde {M}$
of M in
$\widetilde {M}$
of M in
![]() $\operatorname {\mathrm {GL}}_2(\mathbb {Z}/\ell ^a\mathbb {Z})$
satisfies
$\operatorname {\mathrm {GL}}_2(\mathbb {Z}/\ell ^a\mathbb {Z})$
satisfies
![]() $\widetilde {M} \not \equiv I \ \pmod \ell $
. If
$\widetilde {M} \not \equiv I \ \pmod \ell $
. If
![]() $k \not \equiv 1 \ \pmod \ell $
, then
$k \not \equiv 1 \ \pmod \ell $
, then
![]() $\operatorname {det} M \equiv k \ \pmod \ell $
guarantees that
$\operatorname {det} M \equiv k \ \pmod \ell $
guarantees that
![]() $M \not \equiv I \ \pmod {\ell }$
. Since the determinant map
$M \not \equiv I \ \pmod {\ell }$
. Since the determinant map
![]() $\operatorname {det} \colon \operatorname {\mathrm {GL}}_2(\mathbb {Z}/\ell \mathbb {Z}) \to (\mathbb {Z}/\ell \mathbb {Z})^\times $
is a surjective group homomorphism, one can check that there are
$\operatorname {det} \colon \operatorname {\mathrm {GL}}_2(\mathbb {Z}/\ell \mathbb {Z}) \to (\mathbb {Z}/\ell \mathbb {Z})^\times $
is a surjective group homomorphism, one can check that there are
![]() $\ell ^3-\ell $
matrices M in
$\ell ^3-\ell $
matrices M in
![]() $\operatorname {\mathrm {GL}}_2(\mathbb {Z}/\ell \mathbb {Z})$
with
$\operatorname {\mathrm {GL}}_2(\mathbb {Z}/\ell \mathbb {Z})$
with
![]() $\operatorname {det} M \equiv k \ \pmod \ell $
. On the other hand, if
$\operatorname {det} M \equiv k \ \pmod \ell $
. On the other hand, if
![]() $k \equiv 1 \ \pmod \ell $
, we have one less choice for M. Along with Lemma 3.1, we obtain the desired results.
$k \equiv 1 \ \pmod \ell $
, we have one less choice for M. Along with Lemma 3.1, we obtain the desired results.
The next lemma gives a corollary that will be useful when computing the Koblitz constant
![]() $C^{\operatorname {\mathrm {prime}}}_{E,n,k}$
for non-CM curves.
$C^{\operatorname {\mathrm {prime}}}_{E,n,k}$
for non-CM curves.
Lemma 3.3 Let
![]() $\ell $
be an odd prime, t be an integer, and d be an integer coprime to
$\ell $
be an odd prime, t be an integer, and d be an integer coprime to
![]() $\ell $
. Then we have
$\ell $
. Then we have
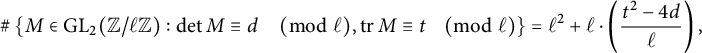 $$ \begin{align*}\#\left\{M \in \operatorname{\mathrm{GL}}_2(\mathbb{Z}/\ell\mathbb{Z}) : \operatorname{det} M \equiv d \quad\pmod \ell, \operatorname{tr} M \equiv t \!\quad\pmod \ell \right\} = \ell^2 + \ell \cdot \left(\frac{t^2-4d}{\ell}\right),\end{align*} $$
$$ \begin{align*}\#\left\{M \in \operatorname{\mathrm{GL}}_2(\mathbb{Z}/\ell\mathbb{Z}) : \operatorname{det} M \equiv d \quad\pmod \ell, \operatorname{tr} M \equiv t \!\quad\pmod \ell \right\} = \ell^2 + \ell \cdot \left(\frac{t^2-4d}{\ell}\right),\end{align*} $$
where
![]() $\left (\frac {\cdot }{\ell }\right )$
denotes the Legendre symbol. If
$\left (\frac {\cdot }{\ell }\right )$
denotes the Legendre symbol. If
![]() $\ell = 2$
, then we have
$\ell = 2$
, then we have
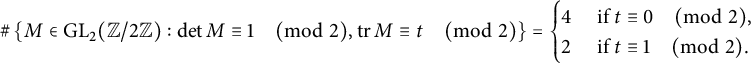 $$ \begin{align*}\#\left\{M \in \operatorname{\mathrm{GL}}_2(\mathbb{Z}/2\mathbb{Z}) : \operatorname{det} M \equiv 1 \quad\pmod 2, \operatorname{tr} M \equiv t \quad\pmod 2 \right\} =\begin{cases} 4 & \text{ if }t \equiv 0 \quad\pmod 2,\\ 2 & \text{ if } t \equiv 1 \quad\pmod 2. \end{cases}\end{align*} $$
$$ \begin{align*}\#\left\{M \in \operatorname{\mathrm{GL}}_2(\mathbb{Z}/2\mathbb{Z}) : \operatorname{det} M \equiv 1 \quad\pmod 2, \operatorname{tr} M \equiv t \quad\pmod 2 \right\} =\begin{cases} 4 & \text{ if }t \equiv 0 \quad\pmod 2,\\ 2 & \text{ if } t \equiv 1 \quad\pmod 2. \end{cases}\end{align*} $$
Proof The case when
![]() $\ell = 2$
follows from a direct calculation. See [Reference Cojocaru, Fouvry and Ram Murty19, Lemma 2.7] for the case when
$\ell = 2$
follows from a direct calculation. See [Reference Cojocaru, Fouvry and Ram Murty19, Lemma 2.7] for the case when
![]() $\ell $
is odd.
$\ell $
is odd.
Corollary 3.4 Fix a prime
![]() $\ell $
and positive integer a. Let k be an integer coprime to
$\ell $
and positive integer a. Let k be an integer coprime to
![]() $\ell $
. Then
$\ell $
. Then
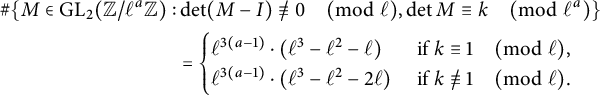 $$ \begin{align*} \#\{M \in \operatorname{\mathrm{GL}}_2(\mathbb{Z}/\ell^a\mathbb{Z}) : &\operatorname{det} (M-I) \not \equiv 0 \quad\pmod \ell, \operatorname{det} M \equiv k \quad\pmod {\ell^a} \} \\ &= \begin{cases} \ell^{3(a-1)} \cdot (\ell^3-\ell^2-\ell) & \text{ if } k \equiv 1 \quad\pmod \ell,\\ \ell^{3(a-1)} \cdot (\ell^3-\ell^2-2\ell) & \text{ if } k \not \equiv 1 \quad\pmod \ell. \end{cases} \end{align*} $$
$$ \begin{align*} \#\{M \in \operatorname{\mathrm{GL}}_2(\mathbb{Z}/\ell^a\mathbb{Z}) : &\operatorname{det} (M-I) \not \equiv 0 \quad\pmod \ell, \operatorname{det} M \equiv k \quad\pmod {\ell^a} \} \\ &= \begin{cases} \ell^{3(a-1)} \cdot (\ell^3-\ell^2-\ell) & \text{ if } k \equiv 1 \quad\pmod \ell,\\ \ell^{3(a-1)} \cdot (\ell^3-\ell^2-2\ell) & \text{ if } k \not \equiv 1 \quad\pmod \ell. \end{cases} \end{align*} $$
Proof Let
![]() $M \in \operatorname {\mathrm {GL}}_2(\mathbb {Z}/\ell ^a\mathbb {Z})$
be such that
$M \in \operatorname {\mathrm {GL}}_2(\mathbb {Z}/\ell ^a\mathbb {Z})$
be such that
![]() $\operatorname {det} M \equiv k \ \pmod {\ell ^a}$
and note that
$\operatorname {det} M \equiv k \ \pmod {\ell ^a}$
and note that
Thus, if
![]() $\ell \neq 2$
, we have that
$\ell \neq 2$
, we have that
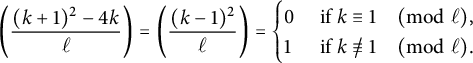 $$ \begin{align*}\left(\frac{(k+1)^2-4k}{\ell}\right) = \left(\frac{(k-1)^2}{\ell}\right) = \begin{cases} 0 & \text{ if } k \equiv 1 \quad\pmod \ell, \\ 1 & \text{ if } k \not \equiv 1 \quad\pmod \ell. \end{cases}\end{align*} $$
$$ \begin{align*}\left(\frac{(k+1)^2-4k}{\ell}\right) = \left(\frac{(k-1)^2}{\ell}\right) = \begin{cases} 0 & \text{ if } k \equiv 1 \quad\pmod \ell, \\ 1 & \text{ if } k \not \equiv 1 \quad\pmod \ell. \end{cases}\end{align*} $$
By Lemma 3.3, this completes the proof when
![]() $\ell \neq 2$
. When
$\ell \neq 2$
. When
![]() $\ell =2$
and
$\ell =2$
and
![]() $a = 1$
, it is straightforward to check that the lemma holds.
$a = 1$
, it is straightforward to check that the lemma holds.
Now, we turn our attention to the CM case. Let K be an imaginary quadratic field and write
![]() $\mathcal {O}_K$
to denote the ring of integers of K. Then
$\mathcal {O}_K$
to denote the ring of integers of K. Then
![]() $\mathcal {O}_K$
is a free
$\mathcal {O}_K$
is a free
![]() $\mathbb {Z}$
-module of rank
$\mathbb {Z}$
-module of rank
![]() $2$
. Fixing a
$2$
. Fixing a
![]() $\mathbb {Z}$
-basis, we can identify
$\mathbb {Z}$
-basis, we can identify
![]() $\operatorname {\mathrm {GL}}_1(\mathcal {O}_K)=\mathcal {O}_K^{\times }$
as a subgroup of
$\operatorname {\mathrm {GL}}_1(\mathcal {O}_K)=\mathcal {O}_K^{\times }$
as a subgroup of
![]() $\operatorname {\mathrm {GL}}_2(\mathbb {Z})$
. In the following discussion (and henceforth) the determinant of g for
$\operatorname {\mathrm {GL}}_2(\mathbb {Z})$
. In the following discussion (and henceforth) the determinant of g for
![]() $g \in \mathcal {O}_K^\times $
means the determinant of g considered as a matrix in
$g \in \mathcal {O}_K^\times $
means the determinant of g considered as a matrix in
![]() $\operatorname {\mathrm {GL}}_2(\mathbb {Z})$
. Moreover, we note that for any odd rational prime
$\operatorname {\mathrm {GL}}_2(\mathbb {Z})$
. Moreover, we note that for any odd rational prime
![]() $\ell $
and integer
$\ell $
and integer
![]() $a\geq 1$
, the determinant of any element in
$a\geq 1$
, the determinant of any element in
![]() $\ell ^a \mathcal {O}_K$
lies in
$\ell ^a \mathcal {O}_K$
lies in
![]() $\ell ^a\mathbb {Z}$
, so we obtain the induced determinant map
$\ell ^a\mathbb {Z}$
, so we obtain the induced determinant map
![]() $\operatorname {det}\colon (\mathcal {O}_K/\ell ^a \mathcal {O}_K)^{\times } \to (\mathbb {Z}/\ell ^a\mathbb {Z})^{\times }$
, which does not depend on the choice of the basis.
$\operatorname {det}\colon (\mathcal {O}_K/\ell ^a \mathcal {O}_K)^{\times } \to (\mathbb {Z}/\ell ^a\mathbb {Z})^{\times }$
, which does not depend on the choice of the basis.
Lemma 3.5 Let K be an imaginary quadratic field and
![]() $\mathcal {O}_K$
be the ring of integers of K. Let
$\mathcal {O}_K$
be the ring of integers of K. Let
![]() $\ell $
be an odd rational prime unramified in K and a be a positive integer. Let k be an integer that is coprime to
$\ell $
be an odd rational prime unramified in K and a be a positive integer. Let k be an integer that is coprime to
![]() $\ell $
and fix
$\ell $
and fix
![]() $g \in (\mathcal {O}_K/\ell \mathcal {O}_K)^\times $
with
$g \in (\mathcal {O}_K/\ell \mathcal {O}_K)^\times $
with
![]() $\operatorname {det} g \equiv k \ \pmod \ell $
. Then
$\operatorname {det} g \equiv k \ \pmod \ell $
. Then
Proof The reduction map
![]() $\pi \colon (\mathcal {O}_K/\ell ^a \mathcal {O}_K)^\times \to (\mathcal {O}_K/\ell \mathcal {O}_K)^\times $
is a surjective group homomorphism. Regardless of whether
$\pi \colon (\mathcal {O}_K/\ell ^a \mathcal {O}_K)^\times \to (\mathcal {O}_K/\ell \mathcal {O}_K)^\times $
is a surjective group homomorphism. Regardless of whether
![]() $\ell $
splits or is inert in K, we have
$\ell $
splits or is inert in K, we have
![]() $|\ker \pi | = \ell ^{2(a-1)}$
by Lemma 2.7. Therefore,
$|\ker \pi | = \ell ^{2(a-1)}$
by Lemma 2.7. Therefore,
The image of
![]() $\pi ^{-1}(g)$
under
$\pi ^{-1}(g)$
under
![]() $\operatorname {det} \colon (\mathcal {O}_K/\ell ^a\mathcal {O}_K)^\times \to (\mathbb {Z}/\ell ^a\mathbb {Z})^\times $
is
$\operatorname {det} \colon (\mathcal {O}_K/\ell ^a\mathcal {O}_K)^\times \to (\mathbb {Z}/\ell ^a\mathbb {Z})^\times $
is
Thus, we have
![]() $\left |\operatorname {det} (\pi ^{-1}(g))\right | = \ell ^{a-1}$
. Finally, note that
$\left |\operatorname {det} (\pi ^{-1}(g))\right | = \ell ^{a-1}$
. Finally, note that
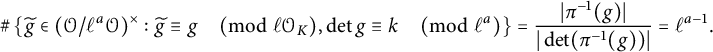 $$ \begin{align*}\#\left\{\widetilde{g} \in (\mathcal{O}/\ell^a\mathcal{O})^\times : \widetilde{g} \equiv g \quad\pmod {\ell\mathcal{O}_K}, \operatorname{det} g \equiv k \quad\pmod {\ell^a} \right\} = \frac{|\pi^{-1}(g)|}{|\operatorname{det}(\pi^{-1}(g))|} = \ell^{a-1}.\end{align*} $$
$$ \begin{align*}\#\left\{\widetilde{g} \in (\mathcal{O}/\ell^a\mathcal{O})^\times : \widetilde{g} \equiv g \quad\pmod {\ell\mathcal{O}_K}, \operatorname{det} g \equiv k \quad\pmod {\ell^a} \right\} = \frac{|\pi^{-1}(g)|}{|\operatorname{det}(\pi^{-1}(g))|} = \ell^{a-1}.\end{align*} $$
We now prove a corollary that will be used for the computation of the Koblitz constant
![]() $C^{\operatorname {\mathrm {prime}}}_{E,n,k}$
for CM curves.
$C^{\operatorname {\mathrm {prime}}}_{E,n,k}$
for CM curves.
Corollary 3.6 Let K be an imaginary quadratic field. Fix an odd rational prime
![]() $\ell $
that is unramified in K. Let k be an integer that is coprime to
$\ell $
that is unramified in K. Let k be an integer that is coprime to
![]() $\ell $
. If
$\ell $
. If
![]() $\ell $
splits in K, then
$\ell $
splits in K, then
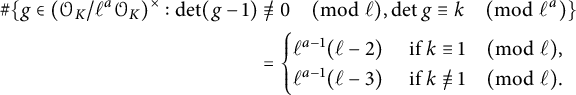 $$ \begin{align*}\#\{ g \in (\mathcal{O}_K/\ell^a\mathcal{O}_K)^\times : \operatorname{det}(g-1) &\not\equiv 0 \quad\pmod \ell, \operatorname{det} g \equiv k \quad\pmod {\ell^a} \} \\ &= \begin{cases} \ell^{a-1}(\ell-2) & \text{ if } k \equiv 1 \quad\pmod \ell, \\ \ell^{a-1}(\ell-3) & \text{ if } k \not \equiv 1 \quad\pmod \ell. \end{cases} \end{align*} $$
$$ \begin{align*}\#\{ g \in (\mathcal{O}_K/\ell^a\mathcal{O}_K)^\times : \operatorname{det}(g-1) &\not\equiv 0 \quad\pmod \ell, \operatorname{det} g \equiv k \quad\pmod {\ell^a} \} \\ &= \begin{cases} \ell^{a-1}(\ell-2) & \text{ if } k \equiv 1 \quad\pmod \ell, \\ \ell^{a-1}(\ell-3) & \text{ if } k \not \equiv 1 \quad\pmod \ell. \end{cases} \end{align*} $$
If
![]() $\ell $
is inert in K, then
$\ell $
is inert in K, then
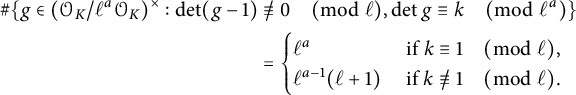 $$ \begin{align*} \#\{ g \in (\mathcal{O}_K/\ell^a\mathcal{O}_K)^\times : \operatorname{det}(g-1) &\not\equiv 0 \quad\pmod {\ell}, \operatorname{det} g \equiv k \quad\pmod {\ell^a} \} \\ &= \begin{cases} \ell^a & \text{ if } k \equiv 1 \quad\pmod \ell, \\ \ell^{a-1}(\ell+1) & \text{ if } k \not \equiv 1 \quad\pmod \ell. \end{cases} \end{align*} $$
$$ \begin{align*} \#\{ g \in (\mathcal{O}_K/\ell^a\mathcal{O}_K)^\times : \operatorname{det}(g-1) &\not\equiv 0 \quad\pmod {\ell}, \operatorname{det} g \equiv k \quad\pmod {\ell^a} \} \\ &= \begin{cases} \ell^a & \text{ if } k \equiv 1 \quad\pmod \ell, \\ \ell^{a-1}(\ell+1) & \text{ if } k \not \equiv 1 \quad\pmod \ell. \end{cases} \end{align*} $$
Proof By Lemma 3.5, it suffices to consider the case where
![]() $a = 1$
. Suppose
$a = 1$
. Suppose
![]() $\ell $
splits in K. Then we have that
$\ell $
splits in K. Then we have that
![]() $\mathcal {O}_K/\ell \mathcal {O}_K \simeq \mathbb {F}_\ell \times \mathbb {F}_\ell $
and the determinant map
$\mathcal {O}_K/\ell \mathcal {O}_K \simeq \mathbb {F}_\ell \times \mathbb {F}_\ell $
and the determinant map
![]() $\operatorname {det} \colon \mathbb {F}_\ell ^{\times } \times \mathbb {F}_\ell ^{\times } \to \mathbb {F}_\ell ^{\times }$
is identified with the multiplication map
$\operatorname {det} \colon \mathbb {F}_\ell ^{\times } \times \mathbb {F}_\ell ^{\times } \to \mathbb {F}_\ell ^{\times }$
is identified with the multiplication map
![]() $(a,b) \mapsto ab$
. Thus, the set in question can be expressed as
$(a,b) \mapsto ab$
. Thus, the set in question can be expressed as
Hence, any element in the set is of the form
![]() $(g,kg^{-1})$
where both g and
$(g,kg^{-1})$
where both g and
![]() $kg^{-1}$
are not congruent to
$kg^{-1}$
are not congruent to
![]() $1$
modulo
$1$
modulo
![]() $\ell $
. Thus, the size of the set is
$\ell $
. Thus, the size of the set is
![]() $\ell -2$
if
$\ell -2$
if
![]() $k \equiv 1 \ \pmod \ell $
and
$k \equiv 1 \ \pmod \ell $
and
![]() $\ell -3$
otherwise.
$\ell -3$
otherwise.
Now, suppose
![]() $\ell $
is inert in K. Then we have
$\ell $
is inert in K. Then we have
![]() $\mathcal {O}_K/\ell \mathcal {O}_K \simeq \mathbb {F}_{\ell ^2}$
and the determinant map
$\mathcal {O}_K/\ell \mathcal {O}_K \simeq \mathbb {F}_{\ell ^2}$
and the determinant map
![]() $\operatorname {det} \colon \mathbb {F}_{\ell ^2} \to \mathbb {F}_\ell $
is identified with the norm map
$\operatorname {det} \colon \mathbb {F}_{\ell ^2} \to \mathbb {F}_\ell $
is identified with the norm map
![]() $N_{\mathbb {F}_{\ell ^2}/\mathbb {F}_\ell }\colon x \mapsto x^{\ell +1}$
. Thus, the set in question can be expressed as
$N_{\mathbb {F}_{\ell ^2}/\mathbb {F}_\ell }\colon x \mapsto x^{\ell +1}$
. Thus, the set in question can be expressed as
For each k coprime to
![]() $\ell $
, there are exactly
$\ell $
, there are exactly
![]() $\ell +1$
choices of
$\ell +1$
choices of
![]() $g \in \mathbb {F}_{\ell ^2}^\times $
with
$g \in \mathbb {F}_{\ell ^2}^\times $
with
![]() $g^{\ell +1} \equiv k \ \pmod \ell $
. In case
$g^{\ell +1} \equiv k \ \pmod \ell $
. In case
![]() $k \equiv 1 \ \pmod \ell $
, we have one less choice due to the constraint
$k \equiv 1 \ \pmod \ell $
, we have one less choice due to the constraint
![]() $(g-1)^{\ell +1} \in \mathbb {F}_\ell ^\times $
.
$(g-1)^{\ell +1} \in \mathbb {F}_\ell ^\times $
.
4 Definitions of the constants
4.1 On the cyclicity constant
We keep the notation from Section 2.1. In this subsection, we introduce the definition of the cyclicity constant
![]() $C_E^{\operatorname {\mathrm {cyc}}}$
, given by Serre, and its average counterpart
$C_E^{\operatorname {\mathrm {cyc}}}$
, given by Serre, and its average counterpart
![]() $C^{\operatorname {\mathrm {cyc}}}$
. For coprime integers n and k, we introduce the cyclicity constant for primes in arithmetic progression
$C^{\operatorname {\mathrm {cyc}}}$
. For coprime integers n and k, we introduce the cyclicity constant for primes in arithmetic progression
![]() $C_{E, n, k}^{\operatorname {\mathrm {cyc}}}$
, given by Akbal and Güloğlu, and its average counterpart
$C_{E, n, k}^{\operatorname {\mathrm {cyc}}}$
, given by Akbal and Güloğlu, and its average counterpart
![]() $C^{\operatorname {\mathrm {cyc}}}_{n, k}$
.
$C^{\operatorname {\mathrm {cyc}}}_{n, k}$
.
First of all, Serre [Reference Serre51, pp. 465–468] defined the cyclicity constant
![]() $C^{\operatorname {\mathrm {cyc}}}_E$
to be
$C^{\operatorname {\mathrm {cyc}}}_E$
to be

where
![]() $\mu (\cdot )$
denotes the Möbius function and
$\mu (\cdot )$
denotes the Möbius function and
![]() $\mathbb {Q}(E[n])$
is the nth division field of E. He proved that, under GRH,
$\mathbb {Q}(E[n])$
is the nth division field of E. He proved that, under GRH,
![]() $C^{\operatorname {\mathrm {cyc}}}_E$
is the density of primes of cyclic reduction for E; see Conjecture 1.1.
$C^{\operatorname {\mathrm {cyc}}}_E$
is the density of primes of cyclic reduction for E; see Conjecture 1.1.
For a non-CM elliptic curve
![]() $E/\mathbb {Q}$
, Jones [Reference Jones31, p. 692] observed that (18) can be expressed as an almost Euler product involving the adelic level of E. Specifically, he showed that
$E/\mathbb {Q}$
, Jones [Reference Jones31, p. 692] observed that (18) can be expressed as an almost Euler product involving the adelic level of E. Specifically, he showed that
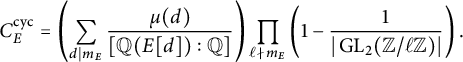 $$ \begin{align} C_E^{\operatorname{\mathrm{cyc}}} = \left(\sum_{d\mid m_E} \frac{\mu(d)}{[\mathbb{Q}(E[d]):\mathbb{Q}]}\right) \prod_{\ell \nmid m_E} \left( 1 - \frac{1}{|\operatorname{\mathrm{GL}}_2(\mathbb{Z}/\ell\mathbb{Z})|}\right). \end{align} $$
$$ \begin{align} C_E^{\operatorname{\mathrm{cyc}}} = \left(\sum_{d\mid m_E} \frac{\mu(d)}{[\mathbb{Q}(E[d]):\mathbb{Q}]}\right) \prod_{\ell \nmid m_E} \left( 1 - \frac{1}{|\operatorname{\mathrm{GL}}_2(\mathbb{Z}/\ell\mathbb{Z})|}\right). \end{align} $$
The average counterpart of
![]() $C^{\operatorname {\mathrm {cyc}}}_E$
is
$C^{\operatorname {\mathrm {cyc}}}_E$
is
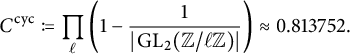
As mentioned in the introduction, Gekeler [Reference Gekeler26] demonstrated that
![]() $C^{\operatorname {\mathrm {cyc}}}$
represents the average cyclicity constant from the local viewpoint. Later, Banks and Shparlinski [Reference Banks and Shparlinski6] verified that the constant also describes the density of primes of cyclic reduction on average in the global sense. Furthermore, Jones [Reference Jones31] verified that the average of
$C^{\operatorname {\mathrm {cyc}}}$
represents the average cyclicity constant from the local viewpoint. Later, Banks and Shparlinski [Reference Banks and Shparlinski6] verified that the constant also describes the density of primes of cyclic reduction on average in the global sense. Furthermore, Jones [Reference Jones31] verified that the average of
![]() $C^{\operatorname {\mathrm {cyc}}}_E$
coincides with
$C^{\operatorname {\mathrm {cyc}}}_E$
coincides with
![]() $C^{\operatorname {\mathrm {cyc}}}$
.
$C^{\operatorname {\mathrm {cyc}}}$
.
Let
![]() $\zeta _n$
denote a primitive nth root of unity, and let
$\zeta _n$
denote a primitive nth root of unity, and let
![]() $\sigma _k \in \operatorname {\mathrm {Gal}}(\mathbb {Q}(\zeta _n)/\mathbb {Q})$
map
$\sigma _k \in \operatorname {\mathrm {Gal}}(\mathbb {Q}(\zeta _n)/\mathbb {Q})$
map
![]() $\zeta _n \mapsto \zeta _n^k$
. Define
$\zeta _n \mapsto \zeta _n^k$
. Define

Akbal and Güloğlu [Reference Akbal and Güloğlu1] defined the constant
![]() $C^{\operatorname {\mathrm {cyc}}}_{E,n,k}$
as follows,
$C^{\operatorname {\mathrm {cyc}}}_{E,n,k}$
as follows,
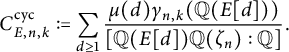
They proved that this constant represents the density of primes
![]() $p \equiv k \ \pmod n$
of cyclic reduction for E, under GRH. Recently, Jones and the first author [Reference Jones and Lee33] demonstrated that for a non-CM elliptic curve
$p \equiv k \ \pmod n$
of cyclic reduction for E, under GRH. Recently, Jones and the first author [Reference Jones and Lee33] demonstrated that for a non-CM elliptic curve
![]() $E/\mathbb {Q}$
, this density can be expressed as an almost Euler product as follows,
$E/\mathbb {Q}$
, this density can be expressed as an almost Euler product as follows,
 $$ \begin{align} C^{\operatorname{\mathrm{cyc}}}_{E,n,k} = \left( \sum_{d\mid m_E} \frac{\mu(d)\gamma_{n,k}(\mathbb{Q}(E[d]))}{[\mathbb{Q}(E[d])\mathbb{Q}(\zeta_n) : \mathbb{Q}]} \right) \prod_{\substack{\ell \nmid m_E \\ \ell \mid (n,k-1)}} \left( 1 - \frac{\phi(\ell)}{|\operatorname{\mathrm{GL}}_2(\mathbb{Z}/\ell\mathbb{Z})|}\right) \prod_{\substack{\ell \nmid nm_E}}\!\left( 1 - \frac{1}{|\operatorname{\mathrm{GL}}_2(\mathbb{Z}/\ell\mathbb{Z})|}\right). \end{align} $$
$$ \begin{align} C^{\operatorname{\mathrm{cyc}}}_{E,n,k} = \left( \sum_{d\mid m_E} \frac{\mu(d)\gamma_{n,k}(\mathbb{Q}(E[d]))}{[\mathbb{Q}(E[d])\mathbb{Q}(\zeta_n) : \mathbb{Q}]} \right) \prod_{\substack{\ell \nmid m_E \\ \ell \mid (n,k-1)}} \left( 1 - \frac{\phi(\ell)}{|\operatorname{\mathrm{GL}}_2(\mathbb{Z}/\ell\mathbb{Z})|}\right) \prod_{\substack{\ell \nmid nm_E}}\!\left( 1 - \frac{1}{|\operatorname{\mathrm{GL}}_2(\mathbb{Z}/\ell\mathbb{Z})|}\right). \end{align} $$
Finally, the average counterpart of
![]() $C^{\operatorname {\mathrm {cyc}}}_{E,n,k}$
is given by
$C^{\operatorname {\mathrm {cyc}}}_{E,n,k}$
is given by
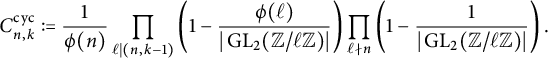
Observe that (23) coincides with (22) if
![]() $m_E$
is taken to be
$m_E$
is taken to be
![]() $1$
. While
$1$
. While
![]() $m_E = 1$
is impossible for any given elliptic curve over
$m_E = 1$
is impossible for any given elliptic curve over
![]() $\mathbb {Q}$
, it is plausible to think that the role of
$\mathbb {Q}$
, it is plausible to think that the role of
![]() $m_E$
is inconsequential when considered over the family of all elliptic curves ordered by height. Indeed, as mentioned in the introduction, the first author [Reference Lee38] demonstrated that
$m_E$
is inconsequential when considered over the family of all elliptic curves ordered by height. Indeed, as mentioned in the introduction, the first author [Reference Lee38] demonstrated that
![]() $C^{\operatorname {\mathrm {cyc}}}_{n,k}$
represents the average density of primes
$C^{\operatorname {\mathrm {cyc}}}_{n,k}$
represents the average density of primes
![]() $p \equiv k \ \pmod n$
of cyclic reduction for the family of elliptic curves ordered by height.
$p \equiv k \ \pmod n$
of cyclic reduction for the family of elliptic curves ordered by height.
We now prove a proposition that serves as a reasonableness check for
![]() $C^{\operatorname {\mathrm {cyc}}}_{n,k}$
. While it can be derived from the main theorem of [Reference Lee38], we opt to include a self-contained proof to draw a parallel with the upcoming Proposition 4.6.
$C^{\operatorname {\mathrm {cyc}}}_{n,k}$
. While it can be derived from the main theorem of [Reference Lee38], we opt to include a self-contained proof to draw a parallel with the upcoming Proposition 4.6.
Proposition 4.1 For any positive integer n, we have
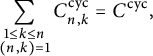 $$ \begin{align*}\sum_{\substack{1 \leq k \leq n \\ (n,k) = 1}}C^{\operatorname{\mathrm{cyc}}}_{n,k} = C^{\operatorname{\mathrm{cyc}}},\end{align*} $$
$$ \begin{align*}\sum_{\substack{1 \leq k \leq n \\ (n,k) = 1}}C^{\operatorname{\mathrm{cyc}}}_{n,k} = C^{\operatorname{\mathrm{cyc}}},\end{align*} $$
where
![]() $C^{\operatorname {\mathrm {cyc}}}$
and
$C^{\operatorname {\mathrm {cyc}}}$
and
![]() $C^{\operatorname {\mathrm {cyc}}}_{n,k}$
are defined in (20) and (23), respectively.
$C^{\operatorname {\mathrm {cyc}}}_{n,k}$
are defined in (20) and (23), respectively.
Proof For notational convenience, we define
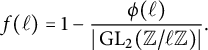 $$ \begin{align*}f(\ell) = 1 - \frac{\phi(\ell)}{|\operatorname{\mathrm{GL}}_2(\mathbb{Z}/\ell\mathbb{Z})|}.\end{align*} $$
$$ \begin{align*}f(\ell) = 1 - \frac{\phi(\ell)}{|\operatorname{\mathrm{GL}}_2(\mathbb{Z}/\ell\mathbb{Z})|}.\end{align*} $$
It suffices to verify that
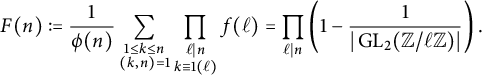
First, we prove that (24) holds for
![]() $n = p^a$
, a prime power. Observe that
$n = p^a$
, a prime power. Observe that
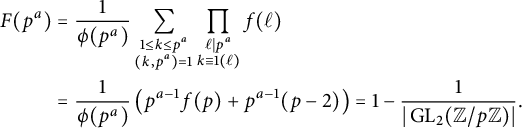 $$ \begin{align*} F(p^a) &= \frac{1}{\phi(p^a)} \sum_{\substack{1\leq k\leq p^a\\ (k,p^a) = 1}} \prod_{\substack{\ell \mid p^a \\ k \equiv 1(\ell)}} f(\ell)\\ &= \frac{1}{\phi(p^a)} \left( p^{a-1} f(p) + p^{a-1}(p-2) \right) = 1 - \frac{1}{|\operatorname{\mathrm{GL}}_2(\mathbb{Z}/p\mathbb{Z})|}. \end{align*} $$
$$ \begin{align*} F(p^a) &= \frac{1}{\phi(p^a)} \sum_{\substack{1\leq k\leq p^a\\ (k,p^a) = 1}} \prod_{\substack{\ell \mid p^a \\ k \equiv 1(\ell)}} f(\ell)\\ &= \frac{1}{\phi(p^a)} \left( p^{a-1} f(p) + p^{a-1}(p-2) \right) = 1 - \frac{1}{|\operatorname{\mathrm{GL}}_2(\mathbb{Z}/p\mathbb{Z})|}. \end{align*} $$
Now, we prove that F is multiplicative. Let
![]() $p^a$
be a prime power and n be a positive integer coprime to p. Then
$p^a$
be a prime power and n be a positive integer coprime to p. Then
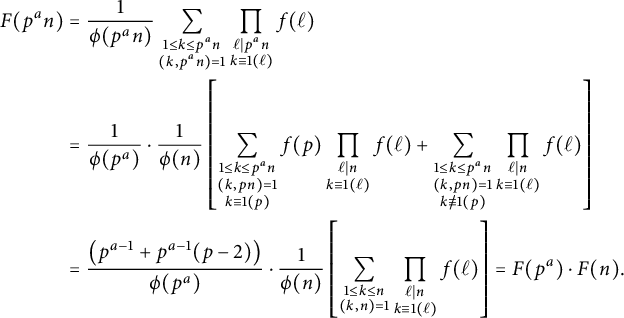 $$ \begin{align*} F(p^an) &= \frac{1}{\phi(p^an)}\sum_{\substack{1 \leq k \leq p^an \\ (k,p^an) = 1}} \prod_{\substack{\ell \mid p^an \\ k \equiv 1 (\ell)}} f(\ell) \\ &= \frac{1}{\phi(p^a)} \cdot \frac{1}{\phi(n)} \left[ \sum_{\substack{1 \leq k \leq p^a n \\ (k,pn) = 1 \\ k \equiv 1 (p)}} f(p) \prod_{\substack{\ell \mid n \\ k \equiv 1 (\ell)}} f(\ell) + \sum_{\substack{1 \leq k \leq p^a n \\ (k,pn) = 1 \\ k \not \equiv 1 (p)}} \prod_{\substack{\ell \mid n \\ k \equiv 1 (\ell)}}f(\ell) \right]\\ &= \frac{\left( p^{a-1} + p^{a-1}(p-2)\right)}{\phi(p^a)} \cdot \frac{1}{\phi(n)} \left[ \sum_{\substack{1 \leq k \leq n \\ (k,n) = 1 }}\prod_{\substack{\ell\mid n \\ k \equiv 1 (\ell)}} f(\ell)\right] = F(p^a) \cdot F(n). \end{align*} $$
$$ \begin{align*} F(p^an) &= \frac{1}{\phi(p^an)}\sum_{\substack{1 \leq k \leq p^an \\ (k,p^an) = 1}} \prod_{\substack{\ell \mid p^an \\ k \equiv 1 (\ell)}} f(\ell) \\ &= \frac{1}{\phi(p^a)} \cdot \frac{1}{\phi(n)} \left[ \sum_{\substack{1 \leq k \leq p^a n \\ (k,pn) = 1 \\ k \equiv 1 (p)}} f(p) \prod_{\substack{\ell \mid n \\ k \equiv 1 (\ell)}} f(\ell) + \sum_{\substack{1 \leq k \leq p^a n \\ (k,pn) = 1 \\ k \not \equiv 1 (p)}} \prod_{\substack{\ell \mid n \\ k \equiv 1 (\ell)}}f(\ell) \right]\\ &= \frac{\left( p^{a-1} + p^{a-1}(p-2)\right)}{\phi(p^a)} \cdot \frac{1}{\phi(n)} \left[ \sum_{\substack{1 \leq k \leq n \\ (k,n) = 1 }}\prod_{\substack{\ell\mid n \\ k \equiv 1 (\ell)}} f(\ell)\right] = F(p^a) \cdot F(n). \end{align*} $$
This completes the proof.
4.2 On the Koblitz constant
We keep the notation from Section 2.1. Now we give the definition of the Koblitz constant
![]() $C_E^{\operatorname {\mathrm {prime}}}$
defined by Zywina and its average counterpart
$C_E^{\operatorname {\mathrm {prime}}}$
defined by Zywina and its average counterpart
![]() $C^{\operatorname {\mathrm {prime}}}$
given by Balog, Cojocaru, and David. Based on Zywina’s method, for coprime integers n and k, we propose the Koblitz constant
$C^{\operatorname {\mathrm {prime}}}$
given by Balog, Cojocaru, and David. Based on Zywina’s method, for coprime integers n and k, we propose the Koblitz constant
![]() $C_{E, n, k}^{\operatorname {\mathrm {prime}}}$
for primes in arithmetic progression and its average counterpart
$C_{E, n, k}^{\operatorname {\mathrm {prime}}}$
for primes in arithmetic progression and its average counterpart
![]() $C_{n, k}^{\operatorname {\mathrm {prime}}}$
.
$C_{n, k}^{\operatorname {\mathrm {prime}}}$
.
Let
![]() $E/\mathbb {Q}$
be a non-CM elliptic curve of conductor
$E/\mathbb {Q}$
be a non-CM elliptic curve of conductor
![]() $N_E$
and m be a positive integer. For
$N_E$
and m be a positive integer. For
![]() $p \nmid mN_E$
, let
$p \nmid mN_E$
, let
![]() $\operatorname {\mathrm {Frob}}_p$
be a Frobenius element at p in
$\operatorname {\mathrm {Frob}}_p$
be a Frobenius element at p in
![]() $\operatorname {\mathrm {Gal}}(\overline {\mathbb {Q}}/\mathbb {Q})$
(see [Reference Serre50, Chapter 2.1, I-6] for the definition of
$\operatorname {\mathrm {Gal}}(\overline {\mathbb {Q}}/\mathbb {Q})$
(see [Reference Serre50, Chapter 2.1, I-6] for the definition of
![]() $\operatorname {\mathrm {Frob}}_p$
). We have that
$\operatorname {\mathrm {Frob}}_p$
). We have that
by [Reference Silverman52, Chapter V. Theorem 2.3.1]. Thus, we see that an odd prime p is of Koblitz reduction if and only if the right-hand side of (25) is invertible modulo m, for every
![]() $m < |\widetilde {E}_p(\mathbb {F}_p)|$
such that
$m < |\widetilde {E}_p(\mathbb {F}_p)|$
such that
![]() $\gcd (p,m) = 1$
.Footnote
4
For such an integer m, we set
$\gcd (p,m) = 1$
.Footnote
4
For such an integer m, we set
Define the ratio
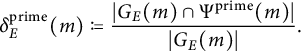
The Koblitz constant, proposed by Zywina [Reference Zywina62], is defined by
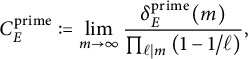
where the limit is taken over all positive integers ordered by divisibility.
We start by proving some properties of
![]() $\delta _E^{\operatorname {\mathrm {prime}}}(\cdot )$
, which were originally remarked in [Reference Zywina62].
$\delta _E^{\operatorname {\mathrm {prime}}}(\cdot )$
, which were originally remarked in [Reference Zywina62].
Proposition 4.2 Let
![]() $E/\mathbb {Q}$
be a non-CM elliptic curve of adelic level
$E/\mathbb {Q}$
be a non-CM elliptic curve of adelic level
![]() $m_E$
. Then
$m_E$
. Then
![]() $\delta _E^{\operatorname {\mathrm {prime}}}(\cdot )$
, as an arithmetic function, satisfies the following properties:
$\delta _E^{\operatorname {\mathrm {prime}}}(\cdot )$
, as an arithmetic function, satisfies the following properties:
-
(1) for any positive integer m,
 $\delta _E^{\operatorname {\mathrm {prime}}}(m) = \delta _E^{\operatorname {\mathrm {prime}}}(\operatorname {\mathrm {rad}}(m))$
;
$\delta _E^{\operatorname {\mathrm {prime}}}(m) = \delta _E^{\operatorname {\mathrm {prime}}}(\operatorname {\mathrm {rad}}(m))$
; -
(2) for any prime
 $\ell \nmid m_E$
and integer d coprime to
$\ell \nmid m_E$
and integer d coprime to
 $\ell $
,
$\ell $
,
 $\delta _E^{\operatorname {\mathrm {prime}}}(d \ell ) = \delta _E^{\operatorname {\mathrm {prime}}}(d) \cdot \delta _E^{\operatorname {\mathrm {prime}}}(\ell )$
.
$\delta _E^{\operatorname {\mathrm {prime}}}(d \ell ) = \delta _E^{\operatorname {\mathrm {prime}}}(d) \cdot \delta _E^{\operatorname {\mathrm {prime}}}(\ell )$
.
Therefore, (27) can be expressed as follows,
 $$ \begin{align} C^{\operatorname{\mathrm{prime}}}_E = \frac{\delta_E^{\operatorname{\mathrm{prime}}}(\operatorname{\mathrm{rad}} (m_E))}{\prod_{\ell \mid m_E} (1-1/\ell)} \cdot \prod_{\ell \nmid m_E} \frac{\delta_{E}^{\operatorname{\mathrm{prime}}}(\ell)}{1-1/\ell}. \end{align} $$
$$ \begin{align} C^{\operatorname{\mathrm{prime}}}_E = \frac{\delta_E^{\operatorname{\mathrm{prime}}}(\operatorname{\mathrm{rad}} (m_E))}{\prod_{\ell \mid m_E} (1-1/\ell)} \cdot \prod_{\ell \nmid m_E} \frac{\delta_{E}^{\operatorname{\mathrm{prime}}}(\ell)}{1-1/\ell}. \end{align} $$
Proof We first prove item (1). Let
![]() $r = \operatorname {\mathrm {rad}}(m)$
and
$r = \operatorname {\mathrm {rad}}(m)$
and
![]() $\varpi \colon G_E(m) \to G_E(r)$
be the usual reduction map. In particular,
$\varpi \colon G_E(m) \to G_E(r)$
be the usual reduction map. In particular,
![]() $\varpi $
is a surjective group homomorphism. We will show that
$\varpi $
is a surjective group homomorphism. We will show that
Let
![]() $M \in G_E(r) \cap \Psi ^{\operatorname {\mathrm {prime}}}(r)$
and
$M \in G_E(r) \cap \Psi ^{\operatorname {\mathrm {prime}}}(r)$
and
![]() $\widetilde {M} \in \varpi ^{-1}(M)$
. Recall that
$\widetilde {M} \in \varpi ^{-1}(M)$
. Recall that
![]() $\operatorname {det}(M-I)$
is invertible modulo r and that m is only supported by the prime factors of r. Thus,
$\operatorname {det}(M-I)$
is invertible modulo r and that m is only supported by the prime factors of r. Thus,
![]() $\operatorname {det}(\widetilde {M}-I)$
is invertible modulo m and
$\operatorname {det}(\widetilde {M}-I)$
is invertible modulo m and
![]() $\widetilde {M} \in G_E(m) \cap \Psi ^{\operatorname {\mathrm {prime}}}(m)$
. The other inclusion is obvious, and hence (29) is obtained. Therefore,
$\widetilde {M} \in G_E(m) \cap \Psi ^{\operatorname {\mathrm {prime}}}(m)$
. The other inclusion is obvious, and hence (29) is obtained. Therefore,
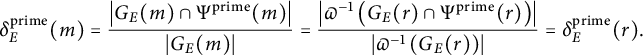 $$ \begin{align*}\delta_E^{\operatorname{\mathrm{prime}}}(m) = \frac{\left| G_E(m) \cap \Psi^{\operatorname{\mathrm{prime}}}(m)\right|}{\left|G_E(m)\right|} = \frac{\left|\varpi^{-1}\left(G_E(r) \cap \Psi^{\operatorname{\mathrm{prime}}}(r)\right)\right|}{\left|\varpi^{-1}\left(G_E(r)\right)\right|} = \delta_E^{\operatorname{\mathrm{prime}}}(r).\end{align*} $$
$$ \begin{align*}\delta_E^{\operatorname{\mathrm{prime}}}(m) = \frac{\left| G_E(m) \cap \Psi^{\operatorname{\mathrm{prime}}}(m)\right|}{\left|G_E(m)\right|} = \frac{\left|\varpi^{-1}\left(G_E(r) \cap \Psi^{\operatorname{\mathrm{prime}}}(r)\right)\right|}{\left|\varpi^{-1}\left(G_E(r)\right)\right|} = \delta_E^{\operatorname{\mathrm{prime}}}(r).\end{align*} $$
We now prove item (2). By Lemma 2.2, we have an isomorphism,
It suffices to show that the isomorphism induces a bijection between the two sets
Take
![]() $M \in G_E(d\ell ) \cap \Psi ^{\operatorname {\mathrm {prime}}}(d\ell )$
. By a similar argument to the proof of (1), we have that
$M \in G_E(d\ell ) \cap \Psi ^{\operatorname {\mathrm {prime}}}(d\ell )$
. By a similar argument to the proof of (1), we have that
![]() $M_d \in G_E(d) \cap \Psi ^{\operatorname {\mathrm {prime}}}(d)$
and
$M_d \in G_E(d) \cap \Psi ^{\operatorname {\mathrm {prime}}}(d)$
and
![]() $M_\ell \in \operatorname {\mathrm {GL}}_2(\mathbb {Z}/\ell \mathbb {Z}) \cap \Psi ^{\operatorname {\mathrm {prime}}}(\ell )$
. Now, let
$M_\ell \in \operatorname {\mathrm {GL}}_2(\mathbb {Z}/\ell \mathbb {Z}) \cap \Psi ^{\operatorname {\mathrm {prime}}}(\ell )$
. Now, let
![]() $M^{\prime } \in G_E(d) \cap \Psi ^{\operatorname {\mathrm {prime}}}(d)$
and
$M^{\prime } \in G_E(d) \cap \Psi ^{\operatorname {\mathrm {prime}}}(d)$
and
![]() $M^{\prime \prime } \in \operatorname {\mathrm {GL}}_2(\mathbb {Z}/\ell \mathbb {Z}) \cap \Psi ^{\operatorname {\mathrm {prime}}}(\ell )$
. Viewing
$M^{\prime \prime } \in \operatorname {\mathrm {GL}}_2(\mathbb {Z}/\ell \mathbb {Z}) \cap \Psi ^{\operatorname {\mathrm {prime}}}(\ell )$
. Viewing
![]() $(M^{\prime },M^{\prime \prime }) \in G_E(d) \times \operatorname {\mathrm {GL}}_2(\mathbb {Z}/\ell \mathbb {Z})$
, there exists a unique element
$(M^{\prime },M^{\prime \prime }) \in G_E(d) \times \operatorname {\mathrm {GL}}_2(\mathbb {Z}/\ell \mathbb {Z})$
, there exists a unique element
![]() $M \in G_E(d\ell )$
with
$M \in G_E(d\ell )$
with
![]() $M_d = M^{\prime }$
and
$M_d = M^{\prime }$
and
![]() $M_\ell = M^{\prime \prime }$
by (30). Since
$M_\ell = M^{\prime \prime }$
by (30). Since
![]() $\operatorname {det}(M^{\prime }-I)\in (\mathbb {Z}/d\mathbb {Z})^{\times }$
and
$\operatorname {det}(M^{\prime }-I)\in (\mathbb {Z}/d\mathbb {Z})^{\times }$
and
![]() $\operatorname {det}(M^{\prime \prime }-I)\in (\mathbb {Z}/\ell \mathbb {Z})^{\times }$
, we have
$\operatorname {det}(M^{\prime \prime }-I)\in (\mathbb {Z}/\ell \mathbb {Z})^{\times }$
, we have
![]() $\operatorname {det}(M-I)\in (\mathbb {Z}/d\ell \mathbb {Z})^{\times }$
; in particular,
$\operatorname {det}(M-I)\in (\mathbb {Z}/d\ell \mathbb {Z})^{\times }$
; in particular,
![]() $M \in \Psi ^{\operatorname {\mathrm {prime}}}(d\ell )$
. Therefore, (31) is established.
$M \in \Psi ^{\operatorname {\mathrm {prime}}}(d\ell )$
. Therefore, (31) is established.
Along with (30), we obtain
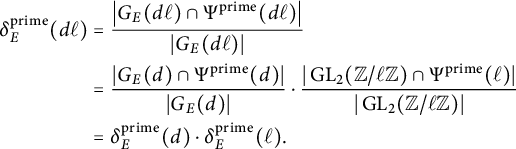 $$ \begin{align*} \delta_{E}^{\operatorname{\mathrm{prime}}}(d\ell) &= \frac{\left|G_E(d\ell)\cap \Psi^{\operatorname{\mathrm{prime}}}(d\ell)\right|}{\left|G_E(d\ell)\right|} \\ &= \frac{|G_E(d) \cap \Psi^{\operatorname{\mathrm{prime}}}(d)|}{|G_E(d)|} \cdot \frac{|\operatorname{\mathrm{GL}}_2(\mathbb{Z}/\ell\mathbb{Z}) \cap \Psi^{\operatorname{\mathrm{prime}}}(\ell)|}{|\operatorname{\mathrm{GL}}_2(\mathbb{Z}/\ell\mathbb{Z})|} \\ &= \delta^{\operatorname{\mathrm{prime}}}_E(d) \cdot \delta^{\operatorname{\mathrm{prime}}}_E(\ell). \end{align*} $$
$$ \begin{align*} \delta_{E}^{\operatorname{\mathrm{prime}}}(d\ell) &= \frac{\left|G_E(d\ell)\cap \Psi^{\operatorname{\mathrm{prime}}}(d\ell)\right|}{\left|G_E(d\ell)\right|} \\ &= \frac{|G_E(d) \cap \Psi^{\operatorname{\mathrm{prime}}}(d)|}{|G_E(d)|} \cdot \frac{|\operatorname{\mathrm{GL}}_2(\mathbb{Z}/\ell\mathbb{Z}) \cap \Psi^{\operatorname{\mathrm{prime}}}(\ell)|}{|\operatorname{\mathrm{GL}}_2(\mathbb{Z}/\ell\mathbb{Z})|} \\ &= \delta^{\operatorname{\mathrm{prime}}}_E(d) \cdot \delta^{\operatorname{\mathrm{prime}}}_E(\ell). \end{align*} $$
This completes the proof.
Remark 4.3 Suppose that
![]() $\ell \nmid m_E$
and
$\ell \nmid m_E$
and
![]() $M \in \operatorname {\mathrm {GL}}_2(\mathbb {Z}/\ell \mathbb {Z})$
. Note that
$M \in \operatorname {\mathrm {GL}}_2(\mathbb {Z}/\ell \mathbb {Z})$
. Note that
![]() $\operatorname {det}(M-I) \in (\mathbb {Z}/\ell \mathbb {Z})^\times $
if and only if
$\operatorname {det}(M-I) \in (\mathbb {Z}/\ell \mathbb {Z})^\times $
if and only if
![]() $1$
is not an eigenvalue of M. One can check from Table 12.4 in [Reference Lang36, Chapter XVIII] that
$1$
is not an eigenvalue of M. One can check from Table 12.4 in [Reference Lang36, Chapter XVIII] that
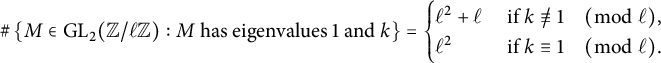 $$ \begin{align*} \#\left\{ M \in \operatorname{\mathrm{GL}}_2(\mathbb{Z}/\ell \mathbb{Z}) : M \text{ has eigenvalues } 1 \text{ and } k \right\} = \begin{cases} \ell^2 + \ell & \text{ if } k \not \equiv 1 \quad\pmod \ell,\\ \ell^2 & \text{ if } k \equiv 1 \quad\pmod \ell. \end{cases} \end{align*} $$
$$ \begin{align*} \#\left\{ M \in \operatorname{\mathrm{GL}}_2(\mathbb{Z}/\ell \mathbb{Z}) : M \text{ has eigenvalues } 1 \text{ and } k \right\} = \begin{cases} \ell^2 + \ell & \text{ if } k \not \equiv 1 \quad\pmod \ell,\\ \ell^2 & \text{ if } k \equiv 1 \quad\pmod \ell. \end{cases} \end{align*} $$
Thus, we see that
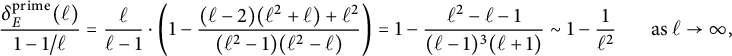 $$ \begin{align} \frac{\delta_E^{\operatorname{\mathrm{prime}}}(\ell)}{1-1/\ell} = \frac{\ell}{\ell-1} \cdot \left(1-\frac{(\ell-2)(\ell^2+\ell) + \ell^2}{(\ell^2-1)(\ell^2-\ell)}\right) = 1 - \frac{\ell^2-\ell-1}{(\ell-1)^3(\ell+1)} \sim 1 - \frac{1}{\ell^2} \hspace{0.5cm} \text{ as } \ell \to \infty, \end{align} $$
$$ \begin{align} \frac{\delta_E^{\operatorname{\mathrm{prime}}}(\ell)}{1-1/\ell} = \frac{\ell}{\ell-1} \cdot \left(1-\frac{(\ell-2)(\ell^2+\ell) + \ell^2}{(\ell^2-1)(\ell^2-\ell)}\right) = 1 - \frac{\ell^2-\ell-1}{(\ell-1)^3(\ell+1)} \sim 1 - \frac{1}{\ell^2} \hspace{0.5cm} \text{ as } \ell \to \infty, \end{align} $$
and hence the infinite product in (28) converges absolutely.
The average counterpart of
![]() $C^{\operatorname {\mathrm {prime}}}_E$
is given by
$C^{\operatorname {\mathrm {prime}}}_E$
is given by
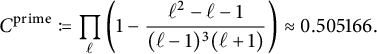
As mentioned earlier, Balog, Cojocaru, and David [Reference Balog, Cojocaru and David5] demonstrated that
![]() $C^{\operatorname {\mathrm {prime}}}$
represents the average Koblitz constant, while Jones [Reference Jones31] verified that the average of
$C^{\operatorname {\mathrm {prime}}}$
represents the average Koblitz constant, while Jones [Reference Jones31] verified that the average of
![]() $C^{\operatorname {\mathrm {prime}}}_E$
coincides with
$C^{\operatorname {\mathrm {prime}}}_E$
coincides with
![]() $C^{\operatorname {\mathrm {prime}}}$
. Unlike for the cyclicity problem, the Koblitz problem has not yet been studied for primes in arithmetic progressions. We construct
$C^{\operatorname {\mathrm {prime}}}$
. Unlike for the cyclicity problem, the Koblitz problem has not yet been studied for primes in arithmetic progressions. We construct
![]() $C^{\operatorname {\mathrm {prime}}}_{E,n,k}$
in a parallel way to Zywina’s method and propose a candidate for the average constant
$C^{\operatorname {\mathrm {prime}}}_{E,n,k}$
in a parallel way to Zywina’s method and propose a candidate for the average constant
![]() $C^{\operatorname {\mathrm {prime}}}_{n,k}$
.
$C^{\operatorname {\mathrm {prime}}}_{n,k}$
.
Let
![]() $E/\mathbb {Q}$
be a non-CM elliptic curve of conductor
$E/\mathbb {Q}$
be a non-CM elliptic curve of conductor
![]() $N_E$
and m be a positive integer. For a prime
$N_E$
and m be a positive integer. For a prime
![]() $p \nmid nN_E$
, let
$p \nmid nN_E$
, let
![]() $\operatorname {\mathrm {Frob}}_p$
be a Frobenius element lying above p in
$\operatorname {\mathrm {Frob}}_p$
be a Frobenius element lying above p in
![]() $\operatorname {\mathrm {Gal}}(\overline {\mathbb {Q}}/\mathbb {Q})$
. We have that
$\operatorname {\mathrm {Gal}}(\overline {\mathbb {Q}}/\mathbb {Q})$
. We have that
Along with (25), let us consider the set
One may note that
![]() $\rho _{E,m}(\operatorname {\mathrm {Frob}}_p) \in G_E(m) \cap \Psi ^{\operatorname {\mathrm {prime}}}_{n,k}(m)$
if and only if
$\rho _{E,m}(\operatorname {\mathrm {Frob}}_p) \in G_E(m) \cap \Psi ^{\operatorname {\mathrm {prime}}}_{n,k}(m)$
if and only if
![]() $p \equiv k \pmod {\gcd (n, m)}$
and
$p \equiv k \pmod {\gcd (n, m)}$
and
![]() $|\widetilde {E}_p(\mathbb {F}_p)|$
is invertible
$|\widetilde {E}_p(\mathbb {F}_p)|$
is invertible
![]() $\mathbb {Z}/m\mathbb {Z}$
. For this reason, we consider the ratio
$\mathbb {Z}/m\mathbb {Z}$
. For this reason, we consider the ratio

Building upon Zywina’s approach, we are led to define
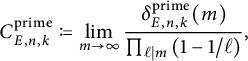
where the limit is taken over all positive integers, ordered by divisibility.
Proposition 4.4 Let
![]() $E/\mathbb {Q}$
be a non-CM elliptic curve of adelic level
$E/\mathbb {Q}$
be a non-CM elliptic curve of adelic level
![]() $m_E$
and n be a positive integer. Let L be defined as in (7). Then,
$m_E$
and n be a positive integer. Let L be defined as in (7). Then,
![]() $\delta _{E,n,k}^{\operatorname {\mathrm {prime}}}(\cdot )$
, as an arithmetic function, satisfies the following properties:
$\delta _{E,n,k}^{\operatorname {\mathrm {prime}}}(\cdot )$
, as an arithmetic function, satisfies the following properties:
-
(1) Let
 $L \mid L^{\prime } \mid L^\infty $
. Then,
$L \mid L^{\prime } \mid L^\infty $
. Then,
 $\delta _{E,n,k}^{\operatorname {\mathrm {prime}}}(L) = \delta _{E,n,k}^{\operatorname {\mathrm {prime}}}(L^{\prime })$
;
$\delta _{E,n,k}^{\operatorname {\mathrm {prime}}}(L) = \delta _{E,n,k}^{\operatorname {\mathrm {prime}}}(L^{\prime })$
; -
(2) Let
 $\ell ^\alpha $
be a prime power and d be a positive integer with
$\ell ^\alpha $
be a prime power and d be a positive integer with
 $(\ell , Ld) = 1$
. Then,
$(\ell , Ld) = 1$
. Then,
 $\delta _{E,n,k}^{\operatorname {\mathrm {prime}}}(d\ell ^a) = \delta _{E,n,k}^{\operatorname {\mathrm {prime}}}(d) \cdot \delta _{E,n,k}^{\operatorname {\mathrm {prime}}}(\ell ^\alpha )$
.
$\delta _{E,n,k}^{\operatorname {\mathrm {prime}}}(d\ell ^a) = \delta _{E,n,k}^{\operatorname {\mathrm {prime}}}(d) \cdot \delta _{E,n,k}^{\operatorname {\mathrm {prime}}}(\ell ^\alpha )$
. -
(3) Let
 $\ell ^\alpha \parallel n$
and
$\ell ^\alpha \parallel n$
and
 $(\ell , L) = 1$
. Then, for any
$(\ell , L) = 1$
. Then, for any
 $\beta> \alpha $
,
$\beta> \alpha $
,
 $\delta ^{\operatorname {\mathrm {prime}}}_{E,n,k}(\ell ^\beta ) = \delta ^{\operatorname {\mathrm {prime}}}_{E,n,k}(\ell ^\alpha )$
. Further, if
$\delta ^{\operatorname {\mathrm {prime}}}_{E,n,k}(\ell ^\beta ) = \delta ^{\operatorname {\mathrm {prime}}}_{E,n,k}(\ell ^\alpha )$
. Further, if
 $\ell \nmid nL$
, we have
$\ell \nmid nL$
, we have
 $\delta _{E,n,k}^{\operatorname {\mathrm {prime}}}(\ell ^\beta ) = \delta ^{\operatorname {\mathrm {prime}}}_E(\ell )$
.
$\delta _{E,n,k}^{\operatorname {\mathrm {prime}}}(\ell ^\beta ) = \delta ^{\operatorname {\mathrm {prime}}}_E(\ell )$
.
Therefore, (35) can be expressed as follows,
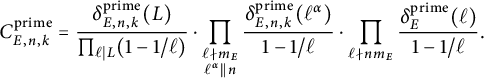 $$ \begin{align} C^{\operatorname{\mathrm{prime}}}_{E,n,k} = \frac{\delta_{E,n,k}^{\operatorname{\mathrm{prime}}}(L)}{\prod_{\ell \mid L}(1-1/\ell)} \cdot \prod_{\substack{\ell \nmid m_E \\ \ell^{\alpha} \parallel n}} \frac{\delta_{E,n,k}^{\operatorname{\mathrm{prime}}}(\ell^{\alpha})}{1-1/\ell} \cdot \prod_{\ell \nmid nm_E} \frac{\delta_E^{\operatorname{\mathrm{prime}}}(\ell)}{1-1/\ell}. \end{align} $$
$$ \begin{align} C^{\operatorname{\mathrm{prime}}}_{E,n,k} = \frac{\delta_{E,n,k}^{\operatorname{\mathrm{prime}}}(L)}{\prod_{\ell \mid L}(1-1/\ell)} \cdot \prod_{\substack{\ell \nmid m_E \\ \ell^{\alpha} \parallel n}} \frac{\delta_{E,n,k}^{\operatorname{\mathrm{prime}}}(\ell^{\alpha})}{1-1/\ell} \cdot \prod_{\ell \nmid nm_E} \frac{\delta_E^{\operatorname{\mathrm{prime}}}(\ell)}{1-1/\ell}. \end{align} $$
and the infinite product converges absolutely.
Proof Let us prove item (1). Consider the natural reduction map
![]() $\varpi \colon G_E(L^{\prime }) \to G_E(L)$
, which is a surjective group homomorphism. We will show that
$\varpi \colon G_E(L^{\prime }) \to G_E(L)$
, which is a surjective group homomorphism. We will show that
Let
![]() $M \in G_E(L) \cap \Psi ^{\operatorname {\mathrm {prime}}}_{n,k}(L)$
and
$M \in G_E(L) \cap \Psi ^{\operatorname {\mathrm {prime}}}_{n,k}(L)$
and
![]() $\widetilde {M} \in \varpi ^{-1}(M)$
. Recall that
$\widetilde {M} \in \varpi ^{-1}(M)$
. Recall that
![]() $\operatorname {det}(M-I)$
is invertible modulo L and that
$\operatorname {det}(M-I)$
is invertible modulo L and that
![]() $L^{\prime }$
is only supported by the prime factors of L. Thus,
$L^{\prime }$
is only supported by the prime factors of L. Thus,
![]() ${\operatorname {det}(\widetilde {M}-I)}$
is invertible modulo
${\operatorname {det}(\widetilde {M}-I)}$
is invertible modulo
![]() $L^{\prime }$
. Since
$L^{\prime }$
. Since
![]() $\gcd (n,L) = \gcd (n,L^{\prime })$
, we also have
$\gcd (n,L) = \gcd (n,L^{\prime })$
, we also have
![]() $\operatorname {det} \widetilde {M} \equiv k \ \pmod {\gcd (n,L^{\prime })}$
. Thus,
$\operatorname {det} \widetilde {M} \equiv k \ \pmod {\gcd (n,L^{\prime })}$
. Thus,
![]() $\widetilde {M} \in G_E(L^{\prime }) \cap \Psi ^{\operatorname {\mathrm {prime}}}_{n,k}(L^{\prime })$
. The other inclusion is obvious, and hence (37) is obtained. Therefore, we have
$\widetilde {M} \in G_E(L^{\prime }) \cap \Psi ^{\operatorname {\mathrm {prime}}}_{n,k}(L^{\prime })$
. The other inclusion is obvious, and hence (37) is obtained. Therefore, we have
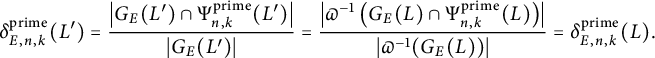 $$ \begin{align*}\delta_{E,n,k}^{\operatorname{\mathrm{prime}}}(L^{\prime}) = \frac{\left|G_E(L^{\prime}) \cap \Psi^{\operatorname{\mathrm{prime}}}_{n,k}(L^{\prime})\right|}{|G_E(L^{\prime})|} = \frac{\left|\varpi^{-1}\left(G_E(L) \cap \Psi^{\operatorname{\mathrm{prime}}}_{n,k}(L)\right)\right|}{|\varpi^{-1}(G_E(L))|} = \delta^{\operatorname{\mathrm{prime}}}_{E,n,k}(L).\end{align*} $$
$$ \begin{align*}\delta_{E,n,k}^{\operatorname{\mathrm{prime}}}(L^{\prime}) = \frac{\left|G_E(L^{\prime}) \cap \Psi^{\operatorname{\mathrm{prime}}}_{n,k}(L^{\prime})\right|}{|G_E(L^{\prime})|} = \frac{\left|\varpi^{-1}\left(G_E(L) \cap \Psi^{\operatorname{\mathrm{prime}}}_{n,k}(L)\right)\right|}{|\varpi^{-1}(G_E(L))|} = \delta^{\operatorname{\mathrm{prime}}}_{E,n,k}(L).\end{align*} $$
Let us prove item (2). By Lemma 2.2, we have an isomorphism,
It suffices to show that the isomorphism induces a map between the sets
Say
![]() $M \in G_E(d\ell ^\alpha ) \cap \Psi ^{\operatorname {\mathrm {prime}}}_{n,k}(d\ell ^\alpha )$
. By a similar argument to the proof of (1), one may see that
$M \in G_E(d\ell ^\alpha ) \cap \Psi ^{\operatorname {\mathrm {prime}}}_{n,k}(d\ell ^\alpha )$
. By a similar argument to the proof of (1), one may see that
![]() $M_d \in G_E(d) \cap \Psi _{n,k}^{\operatorname {\mathrm {prime}}}(d)$
and
$M_d \in G_E(d) \cap \Psi _{n,k}^{\operatorname {\mathrm {prime}}}(d)$
and
![]() $M_{\ell ^\alpha } \in \operatorname {\mathrm {GL}}_2(\mathbb {Z}/\ell ^\alpha \mathbb {Z}) \cap \Psi _{n,k}^{\operatorname {\mathrm {prime}}}(\ell ^\alpha )$
. Now, let
$M_{\ell ^\alpha } \in \operatorname {\mathrm {GL}}_2(\mathbb {Z}/\ell ^\alpha \mathbb {Z}) \cap \Psi _{n,k}^{\operatorname {\mathrm {prime}}}(\ell ^\alpha )$
. Now, let
![]() $M^{\prime } \in G_E(d) \cap \Psi ^{\operatorname {\mathrm {prime}}}(d)$
and
$M^{\prime } \in G_E(d) \cap \Psi ^{\operatorname {\mathrm {prime}}}(d)$
and
![]() $M^{\prime \prime } \in \operatorname {\mathrm {GL}}_2(\mathbb {Z}/\ell ^\alpha \mathbb {Z}) \cap \Psi ^{\operatorname {\mathrm {prime}}}(\ell ^\alpha )$
. Viewing
$M^{\prime \prime } \in \operatorname {\mathrm {GL}}_2(\mathbb {Z}/\ell ^\alpha \mathbb {Z}) \cap \Psi ^{\operatorname {\mathrm {prime}}}(\ell ^\alpha )$
. Viewing
![]() $(M^{\prime },M^{\prime \prime }) \in G_E(d) \times \operatorname {\mathrm {GL}}_2(\mathbb {Z}/\ell ^\alpha \mathbb {Z})$
, there exists a unique element
$(M^{\prime },M^{\prime \prime }) \in G_E(d) \times \operatorname {\mathrm {GL}}_2(\mathbb {Z}/\ell ^\alpha \mathbb {Z})$
, there exists a unique element
![]() $M \in G_E(d\ell ^\alpha )$
with
$M \in G_E(d\ell ^\alpha )$
with
![]() $M_d = M^{\prime }$
and
$M_d = M^{\prime }$
and
![]() $M_{\ell ^\alpha } = M^{\prime \prime }$
by (38). Note that since
$M_{\ell ^\alpha } = M^{\prime \prime }$
by (38). Note that since
![]() $\operatorname {det}(M^{\prime }-I)\in (\mathbb {Z}/d\mathbb {Z})^{\times }$
and
$\operatorname {det}(M^{\prime }-I)\in (\mathbb {Z}/d\mathbb {Z})^{\times }$
and
![]() $\operatorname {det}(M^{\prime \prime }-I)\in (\mathbb {Z}/\ell ^{\alpha }\mathbb {Z})^{\times }$
, we have
$\operatorname {det}(M^{\prime \prime }-I)\in (\mathbb {Z}/\ell ^{\alpha }\mathbb {Z})^{\times }$
, we have
![]() $\operatorname {det}(M-I)\in (\mathbb {Z}/d\ell ^{\alpha }\mathbb {Z})^{\times }$
; in particular,
$\operatorname {det}(M-I)\in (\mathbb {Z}/d\ell ^{\alpha }\mathbb {Z})^{\times }$
; in particular,
![]() $M \in \Psi ^{\operatorname {\mathrm {prime}}}_{n,k}(d\ell ^\alpha )$
. Therefore, (39) is established.
$M \in \Psi ^{\operatorname {\mathrm {prime}}}_{n,k}(d\ell ^\alpha )$
. Therefore, (39) is established.
Along with (38), we obtain
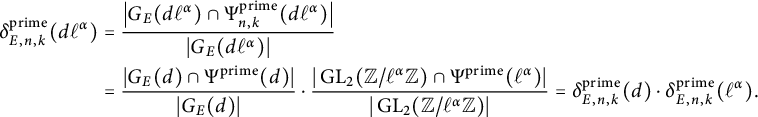 $$ \begin{align*} \delta_{E,n,k}^{\operatorname{\mathrm{prime}}}(d\ell^\alpha) &= \frac{\left|G_E(d\ell^\alpha)\cap \Psi^{\operatorname{\mathrm{prime}}}_{n,k}(d\ell^\alpha)\right|}{\left|G_E(d\ell^\alpha)\right|} \\ &= \frac{|G_E(d) \cap \Psi^{\operatorname{\mathrm{prime}}}(d)|}{|G_E(d)|} \cdot \frac{|\operatorname{\mathrm{GL}}_2(\mathbb{Z}/\ell^\alpha\mathbb{Z}) \cap \Psi^{\operatorname{\mathrm{prime}}}(\ell^\alpha)|}{|\operatorname{\mathrm{GL}}_2(\mathbb{Z}/\ell^\alpha\mathbb{Z})|} = \delta^{\operatorname{\mathrm{prime}}}_{E,n,k}(d) \cdot \delta^{\operatorname{\mathrm{prime}}}_{E,n,k}(\ell^\alpha). \end{align*} $$
$$ \begin{align*} \delta_{E,n,k}^{\operatorname{\mathrm{prime}}}(d\ell^\alpha) &= \frac{\left|G_E(d\ell^\alpha)\cap \Psi^{\operatorname{\mathrm{prime}}}_{n,k}(d\ell^\alpha)\right|}{\left|G_E(d\ell^\alpha)\right|} \\ &= \frac{|G_E(d) \cap \Psi^{\operatorname{\mathrm{prime}}}(d)|}{|G_E(d)|} \cdot \frac{|\operatorname{\mathrm{GL}}_2(\mathbb{Z}/\ell^\alpha\mathbb{Z}) \cap \Psi^{\operatorname{\mathrm{prime}}}(\ell^\alpha)|}{|\operatorname{\mathrm{GL}}_2(\mathbb{Z}/\ell^\alpha\mathbb{Z})|} = \delta^{\operatorname{\mathrm{prime}}}_{E,n,k}(d) \cdot \delta^{\operatorname{\mathrm{prime}}}_{E,n,k}(\ell^\alpha). \end{align*} $$
Finally, let us prove item (3). Since
![]() $\ell \nmid m_E$
, by Lemma 2.2,
$\ell \nmid m_E$
, by Lemma 2.2,
![]() $G_E(\ell ^\alpha )$
and
$G_E(\ell ^\alpha )$
and
![]() $G_E(\ell ^\beta )$
are the full groups,
$G_E(\ell ^\beta )$
are the full groups,
![]() $\operatorname {\mathrm {GL}}_2(\mathbb {Z}/\ell ^\alpha \mathbb {Z})$
and
$\operatorname {\mathrm {GL}}_2(\mathbb {Z}/\ell ^\alpha \mathbb {Z})$
and
![]() $\operatorname {\mathrm {GL}}_2(\mathbb {Z}/\ell ^\beta \mathbb {Z})$
. Let
$\operatorname {\mathrm {GL}}_2(\mathbb {Z}/\ell ^\beta \mathbb {Z})$
. Let
![]() $\varpi \colon \operatorname {\mathrm {GL}}_2(\mathbb {Z}/\ell ^\beta \mathbb {Z}) \to \operatorname {\mathrm {GL}}_2(\mathbb {Z}/\ell ^\alpha \mathbb {Z})$
be the natural reduction map which is a surjective group homomorphism. By a similar argument as in the proof of item (1), it suffices to check that
$\varpi \colon \operatorname {\mathrm {GL}}_2(\mathbb {Z}/\ell ^\beta \mathbb {Z}) \to \operatorname {\mathrm {GL}}_2(\mathbb {Z}/\ell ^\alpha \mathbb {Z})$
be the natural reduction map which is a surjective group homomorphism. By a similar argument as in the proof of item (1), it suffices to check that
Take
![]() $M \in \Psi ^{\operatorname {\mathrm {prime}}}_{n,k}(\ell ^\alpha )$
and let
$M \in \Psi ^{\operatorname {\mathrm {prime}}}_{n,k}(\ell ^\alpha )$
and let
![]() $\widetilde {M} \in \varpi ^{-1}(M)$
. By the same reasoning in the proof of item (1),
$\widetilde {M} \in \varpi ^{-1}(M)$
. By the same reasoning in the proof of item (1),
![]() $\operatorname {det}(\widetilde {M}-I)$
is invertible modulo
$\operatorname {det}(\widetilde {M}-I)$
is invertible modulo
![]() $\ell ^\beta $
. Since
$\ell ^\beta $
. Since
![]() $\gcd (n,\ell ^\alpha ) = \gcd (n,\ell ^\beta ) = \ell ^\alpha $
, we also have
$\gcd (n,\ell ^\alpha ) = \gcd (n,\ell ^\beta ) = \ell ^\alpha $
, we also have
![]() $\operatorname {det} \widetilde {M} \equiv k \ \pmod {\ell ^\alpha }$
. The other inclusion is obvious, and hence (40) is obtained. Thus, we have
$\operatorname {det} \widetilde {M} \equiv k \ \pmod {\ell ^\alpha }$
. The other inclusion is obvious, and hence (40) is obtained. Thus, we have
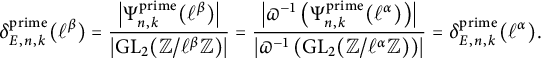 $$ \begin{align*}\delta_{E,n,k}^{\operatorname{\mathrm{prime}}}(\ell^\beta) = \frac{\left|\Psi^{\operatorname{\mathrm{prime}}}_{n,k}(\ell^\beta)\right|}{\left|\operatorname{\mathrm{GL}}_2(\mathbb{Z}/\ell^\beta\mathbb{Z})\right|} = \frac{\left|\varpi^{-1}\left(\Psi^{\operatorname{\mathrm{prime}}}_{n,k}(\ell^\alpha)\right) \right|}{\left| \varpi^{-1}\left(\operatorname{\mathrm{GL}}_2(\mathbb{Z}/\ell^\alpha\mathbb{Z})\right)\right|} = \delta_{E,n,k}^{\operatorname{\mathrm{prime}}}(\ell^\alpha).\end{align*} $$
$$ \begin{align*}\delta_{E,n,k}^{\operatorname{\mathrm{prime}}}(\ell^\beta) = \frac{\left|\Psi^{\operatorname{\mathrm{prime}}}_{n,k}(\ell^\beta)\right|}{\left|\operatorname{\mathrm{GL}}_2(\mathbb{Z}/\ell^\beta\mathbb{Z})\right|} = \frac{\left|\varpi^{-1}\left(\Psi^{\operatorname{\mathrm{prime}}}_{n,k}(\ell^\alpha)\right) \right|}{\left| \varpi^{-1}\left(\operatorname{\mathrm{GL}}_2(\mathbb{Z}/\ell^\alpha\mathbb{Z})\right)\right|} = \delta_{E,n,k}^{\operatorname{\mathrm{prime}}}(\ell^\alpha).\end{align*} $$
In case
![]() $\ell \nmid nL$
, let
$\ell \nmid nL$
, let
![]() $\varpi \colon \operatorname {\mathrm {GL}}_2(\mathbb {Z}/\ell ^\beta \mathbb {Z}) \to \operatorname {\mathrm {GL}}_2(\mathbb {Z}/\ell \mathbb {Z})$
. It suffices to check
$\varpi \colon \operatorname {\mathrm {GL}}_2(\mathbb {Z}/\ell ^\beta \mathbb {Z}) \to \operatorname {\mathrm {GL}}_2(\mathbb {Z}/\ell \mathbb {Z})$
. It suffices to check
Note that the condition
![]() $\operatorname {det} M \equiv k \ \pmod {\gcd (n,\ell )}$
is trivial, and hence
$\operatorname {det} M \equiv k \ \pmod {\gcd (n,\ell )}$
is trivial, and hence
![]() $\Psi ^{\operatorname {\mathrm {prime}}}_{E,n,k}(\ell ) = \Psi ^{\operatorname {\mathrm {prime}}}_E(\ell )$
. Let
$\Psi ^{\operatorname {\mathrm {prime}}}_{E,n,k}(\ell ) = \Psi ^{\operatorname {\mathrm {prime}}}_E(\ell )$
. Let
![]() $M \in \Psi ^{\operatorname {\mathrm {prime}}}_E(\ell )$
. Note that every lifting
$M \in \Psi ^{\operatorname {\mathrm {prime}}}_E(\ell )$
. Note that every lifting
![]() $\widetilde {M} \in \varpi ^{-1}(M)$
belongs to
$\widetilde {M} \in \varpi ^{-1}(M)$
belongs to
![]() $\Psi ^{\operatorname {\mathrm {prime}}}_{E,n,k}(\ell ^\beta )$
. The other inclusion is obvious, and hence (41) is obtained. Thus, we have
$\Psi ^{\operatorname {\mathrm {prime}}}_{E,n,k}(\ell ^\beta )$
. The other inclusion is obvious, and hence (41) is obtained. Thus, we have
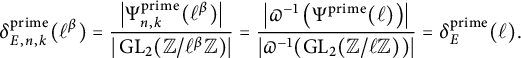 $$ \begin{align*}\delta_{E,n,k}^{\operatorname{\mathrm{prime}}}(\ell^\beta) = \frac{\left|\Psi^{\operatorname{\mathrm{prime}}}_{n,k}(\ell^\beta)\right|}{|\operatorname{\mathrm{GL}}_2(\mathbb{Z}/\ell^\beta\mathbb{Z})|} = \frac{\left|\varpi^{-1}\left(\Psi^{\operatorname{\mathrm{prime}}}(\ell)\right)\right|}{\left|\varpi^{-1}(\operatorname{\mathrm{GL}}_2(\mathbb{Z}/\ell\mathbb{Z}))\right|} = \delta_E^{\operatorname{\mathrm{prime}}}(\ell).\end{align*} $$
$$ \begin{align*}\delta_{E,n,k}^{\operatorname{\mathrm{prime}}}(\ell^\beta) = \frac{\left|\Psi^{\operatorname{\mathrm{prime}}}_{n,k}(\ell^\beta)\right|}{|\operatorname{\mathrm{GL}}_2(\mathbb{Z}/\ell^\beta\mathbb{Z})|} = \frac{\left|\varpi^{-1}\left(\Psi^{\operatorname{\mathrm{prime}}}(\ell)\right)\right|}{\left|\varpi^{-1}(\operatorname{\mathrm{GL}}_2(\mathbb{Z}/\ell\mathbb{Z}))\right|} = \delta_E^{\operatorname{\mathrm{prime}}}(\ell).\end{align*} $$
By grouping the prime factors of M in (35) according to whether they divide L or not, we obtain (36). The absolute convergence of (36) follows from Remark 4.3.
The following lemma allows us to express
![]() $C_{E,n,k}^{\operatorname {\mathrm {prime}}}$
more explicitly.
$C_{E,n,k}^{\operatorname {\mathrm {prime}}}$
more explicitly.
Lemma 4.5 Suppose
![]() $\ell ^{\alpha } \parallel n$
and
$\ell ^{\alpha } \parallel n$
and
![]() $\ell \nmid m_E$
. Then
$\ell \nmid m_E$
. Then
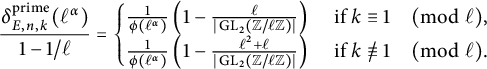 $$ \begin{align*} \frac{\delta_{E,n,k}^{\operatorname{\mathrm{prime}}}(\ell^{\alpha})}{1-1/\ell} = \begin{cases} \frac{1}{\phi(\ell^{\alpha})} \left( 1 - \frac{\ell}{|\operatorname{\mathrm{GL}}_2(\mathbb{Z}/\ell\mathbb{Z})|}\right) & \text{ if } k \equiv 1 \quad\pmod \ell, \\ \frac{1}{\phi(\ell^{\alpha})}\left( 1 - \frac{\ell^2+\ell}{|\operatorname{\mathrm{GL}}_2(\mathbb{Z}/\ell\mathbb{Z})|}\right) & \text{ if } k \not \equiv 1 \quad\pmod \ell. \end{cases} \end{align*} $$
$$ \begin{align*} \frac{\delta_{E,n,k}^{\operatorname{\mathrm{prime}}}(\ell^{\alpha})}{1-1/\ell} = \begin{cases} \frac{1}{\phi(\ell^{\alpha})} \left( 1 - \frac{\ell}{|\operatorname{\mathrm{GL}}_2(\mathbb{Z}/\ell\mathbb{Z})|}\right) & \text{ if } k \equiv 1 \quad\pmod \ell, \\ \frac{1}{\phi(\ell^{\alpha})}\left( 1 - \frac{\ell^2+\ell}{|\operatorname{\mathrm{GL}}_2(\mathbb{Z}/\ell\mathbb{Z})|}\right) & \text{ if } k \not \equiv 1 \quad\pmod \ell. \end{cases} \end{align*} $$
Proof By the assumption, we have
![]() $G_E(\ell ^{\alpha }) \simeq \operatorname {\mathrm {GL}}_2(\mathbb {Z}/\ell ^{\alpha }\mathbb {Z})$
. Recall that
$G_E(\ell ^{\alpha }) \simeq \operatorname {\mathrm {GL}}_2(\mathbb {Z}/\ell ^{\alpha }\mathbb {Z})$
. Recall that
whose cardinality was determined in Corollary 3.4. A brief calculation reveals the desired result.
Let
![]() $E/\mathbb {Q}$
be a non-CM elliptic curve of adelic level
$E/\mathbb {Q}$
be a non-CM elliptic curve of adelic level
![]() $m_E$
. Let
$m_E$
. Let
![]() $n = n_1n_2$
where
$n = n_1n_2$
where
![]() $n_1 = \gcd (n,m_E^\infty )$
and
$n_1 = \gcd (n,m_E^\infty )$
and
![]() $(n_2,m_E) = 1$
. By (32), (36), and Lemma 4.5, we have
$(n_2,m_E) = 1$
. By (32), (36), and Lemma 4.5, we have
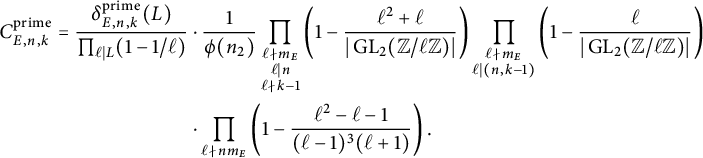 $$ \begin{align*} \begin{split} C^{\operatorname{\mathrm{prime}}}_{E,n,k} = \frac{\delta^{\operatorname{\mathrm{prime}}}_{E,n,k}(L)}{\prod_{\ell \mid L}(1-1/\ell)} & \cdot \frac{1}{\phi(n_2)} \prod_{\substack{\ell \nmid m_E \\ \ell \mid n \\ \ell \nmid k-1}} \left( 1 - \frac{\ell^2+\ell}{|\operatorname{\mathrm{GL}}_2(\mathbb{Z}/\ell\mathbb{Z})|}\right) \prod_{\substack{\ell \nmid m_E \\ \ell \mid (n,k-1)}} \left( 1 - \frac{\ell}{|\operatorname{\mathrm{GL}}_2(\mathbb{Z}/\ell\mathbb{Z})|}\right) \\ &\cdot \prod_{\ell \nmid nm_E}\left( 1 - \frac{\ell^2-\ell-1}{(\ell-1)^3(\ell+1)}\right). \end{split} \end{align*} $$
$$ \begin{align*} \begin{split} C^{\operatorname{\mathrm{prime}}}_{E,n,k} = \frac{\delta^{\operatorname{\mathrm{prime}}}_{E,n,k}(L)}{\prod_{\ell \mid L}(1-1/\ell)} & \cdot \frac{1}{\phi(n_2)} \prod_{\substack{\ell \nmid m_E \\ \ell \mid n \\ \ell \nmid k-1}} \left( 1 - \frac{\ell^2+\ell}{|\operatorname{\mathrm{GL}}_2(\mathbb{Z}/\ell\mathbb{Z})|}\right) \prod_{\substack{\ell \nmid m_E \\ \ell \mid (n,k-1)}} \left( 1 - \frac{\ell}{|\operatorname{\mathrm{GL}}_2(\mathbb{Z}/\ell\mathbb{Z})|}\right) \\ &\cdot \prod_{\ell \nmid nm_E}\left( 1 - \frac{\ell^2-\ell-1}{(\ell-1)^3(\ell+1)}\right). \end{split} \end{align*} $$
We now propose the average counterpart of
![]() $C^{\operatorname {\mathrm {prime}}}_{E,n,k}$
,
$C^{\operatorname {\mathrm {prime}}}_{E,n,k}$
,
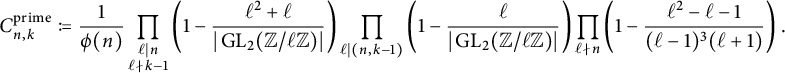
The formula for
![]() $C_{n,k}^{\operatorname {\mathrm {prime}}}$
coincides with
$C_{n,k}^{\operatorname {\mathrm {prime}}}$
coincides with
![]() $C^{\operatorname {\mathrm {prime}}}_{E,n,k}$
if one takes
$C^{\operatorname {\mathrm {prime}}}_{E,n,k}$
if one takes
![]() $m_E = 1$
, similar to the case for
$m_E = 1$
, similar to the case for
![]() $C_{n,k}^{\operatorname {\mathrm {cyc}}}$
in (23). Parallel to Proposition 4.1, we show that
$C_{n,k}^{\operatorname {\mathrm {cyc}}}$
in (23). Parallel to Proposition 4.1, we show that
![]() $C_{n,k}^{\operatorname {\mathrm {prime}}}$
behaves as expected when we sum over k.
$C_{n,k}^{\operatorname {\mathrm {prime}}}$
behaves as expected when we sum over k.
Proposition 4.6 For any positive integer n, we have
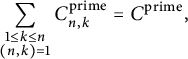 $$ \begin{align*}\sum_{\substack{1 \leq k \leq n \\ (n,k) = 1}}C^{\operatorname{\mathrm{prime}}}_{n,k} = C^{\operatorname{\mathrm{prime}}},\end{align*} $$
$$ \begin{align*}\sum_{\substack{1 \leq k \leq n \\ (n,k) = 1}}C^{\operatorname{\mathrm{prime}}}_{n,k} = C^{\operatorname{\mathrm{prime}}},\end{align*} $$
where
![]() $C^{\operatorname {\mathrm {prime}}}$
and
$C^{\operatorname {\mathrm {prime}}}$
and
![]() $C^{\operatorname {\mathrm {prime}}}_{n,k}$
are defined in (33) and (42), respectively.
$C^{\operatorname {\mathrm {prime}}}_{n,k}$
are defined in (33) and (42), respectively.
Proof For notational convenience, we define
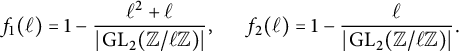 $$ \begin{align*}f_1(\ell) = 1 - \frac{\ell^2+\ell}{|\operatorname{\mathrm{GL}}_2(\mathbb{Z}/\ell\mathbb{Z})|}, \hspace{0.5cm} f_2(\ell) = 1 - \frac{\ell}{|\operatorname{\mathrm{GL}}_2(\mathbb{Z}/\ell\mathbb{Z})|}.\end{align*} $$
$$ \begin{align*}f_1(\ell) = 1 - \frac{\ell^2+\ell}{|\operatorname{\mathrm{GL}}_2(\mathbb{Z}/\ell\mathbb{Z})|}, \hspace{0.5cm} f_2(\ell) = 1 - \frac{\ell}{|\operatorname{\mathrm{GL}}_2(\mathbb{Z}/\ell\mathbb{Z})|}.\end{align*} $$
To show the desired equation, we need to verify that
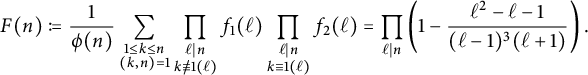
First, we prove that (43) is true for
![]() $n = p^a$
, a prime power. Observe that
$n = p^a$
, a prime power. Observe that
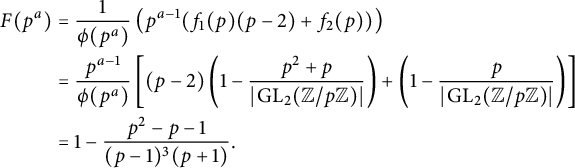 $$ \begin{align*} F(p^a) &= \frac{1}{\phi(p^a)}\left(p^{a-1}(f_1(p)(p-2) + f_2(p))\right)\\ &= \frac{p^{a-1}}{\phi(p^a)} \left[ (p-2)\left( 1 - \frac{p^2+p}{|\operatorname{\mathrm{GL}}_2(\mathbb{Z}/p\mathbb{Z})|}\right) + \left( 1 - \frac{p}{|\operatorname{\mathrm{GL}}_2(\mathbb{Z}/p\mathbb{Z})|}\right) \right] \\ &= 1 - \frac{p^2-p-1}{(p-1)^3(p+1)}. \end{align*} $$
$$ \begin{align*} F(p^a) &= \frac{1}{\phi(p^a)}\left(p^{a-1}(f_1(p)(p-2) + f_2(p))\right)\\ &= \frac{p^{a-1}}{\phi(p^a)} \left[ (p-2)\left( 1 - \frac{p^2+p}{|\operatorname{\mathrm{GL}}_2(\mathbb{Z}/p\mathbb{Z})|}\right) + \left( 1 - \frac{p}{|\operatorname{\mathrm{GL}}_2(\mathbb{Z}/p\mathbb{Z})|}\right) \right] \\ &= 1 - \frac{p^2-p-1}{(p-1)^3(p+1)}. \end{align*} $$
Let us prove that F is multiplicative. Let n be coprime to
![]() $p^a$
, a prime power. We see that
$p^a$
, a prime power. We see that
 $$ \begin{align*} F(p^an) &= \frac{1}{\phi(p^an)}\sum_{\substack{1 \leq k \leq p^a n \\ (k,pn) = 1}} \prod_{\substack{\ell \mid pn \\ k \not \equiv 1 (\ell)}}f_1(\ell) \prod_{\substack{\ell \mid pn \\ k \equiv 1 (\ell)}}f_2(\ell) \\ &= \frac{1}{\phi(p^a)} \frac{1}{\phi(n)}\left[\sum_{\substack{1 \leq k \leq p^an \\ (k,pn) = 1 \\ k \not \equiv 1 (p)}}f_1(p) \prod_{\substack{\ell \mid n \\ k \not \equiv 1(\ell)}}f_1(\ell) \prod_{\substack{\ell \mid n \\ k \equiv 1 (\ell)}} f_2(\ell) + \sum_{\substack{1 \leq k \leq p^an \\ (k,pn) = 1 \\ k \equiv 1 (p)}} f_2(p) \prod_{\substack{\ell \mid n \\ k \not \equiv 1 (\ell)}} f_1(\ell) \prod_{\substack{\ell \mid n \\ k \equiv 1(\ell)}}f_2(\ell)\right] \\ &= \frac{f_1(p) (p-2)p^{a-1}}{\phi(p^a)} \frac{1}{\phi(n)}\sum_{\substack{1 \leq k \leq n \\ (k,n) = 1}} \prod_{\substack{\ell \mid n \\ k \not \equiv 1 (\ell)}} f_1(\ell) \prod_{\substack{\ell \mid n \\ k \equiv 1 (\ell)}}f_2(\ell) \\ &\hspace{1in} + \frac{f_2(p) p^{a-1}}{\phi(p^a)} \frac{1}{\phi(n)} \sum_{\substack{1 \leq k \leq n \\ (k,n) = 1}} \prod_{\substack{\ell \mid n \\ k \not \equiv 1 (\ell)}} f_1(\ell) \prod_{\substack{\ell \mid n \\ k \equiv 1 (\ell)}}f_2(\ell) \\ &=\frac{1}{\phi(p^a)}\left(p^{a-1}(f_1(p)(p-2) + f_2(p))\right) \cdot F(n) = F(p^a)F(n). \end{align*} $$
$$ \begin{align*} F(p^an) &= \frac{1}{\phi(p^an)}\sum_{\substack{1 \leq k \leq p^a n \\ (k,pn) = 1}} \prod_{\substack{\ell \mid pn \\ k \not \equiv 1 (\ell)}}f_1(\ell) \prod_{\substack{\ell \mid pn \\ k \equiv 1 (\ell)}}f_2(\ell) \\ &= \frac{1}{\phi(p^a)} \frac{1}{\phi(n)}\left[\sum_{\substack{1 \leq k \leq p^an \\ (k,pn) = 1 \\ k \not \equiv 1 (p)}}f_1(p) \prod_{\substack{\ell \mid n \\ k \not \equiv 1(\ell)}}f_1(\ell) \prod_{\substack{\ell \mid n \\ k \equiv 1 (\ell)}} f_2(\ell) + \sum_{\substack{1 \leq k \leq p^an \\ (k,pn) = 1 \\ k \equiv 1 (p)}} f_2(p) \prod_{\substack{\ell \mid n \\ k \not \equiv 1 (\ell)}} f_1(\ell) \prod_{\substack{\ell \mid n \\ k \equiv 1(\ell)}}f_2(\ell)\right] \\ &= \frac{f_1(p) (p-2)p^{a-1}}{\phi(p^a)} \frac{1}{\phi(n)}\sum_{\substack{1 \leq k \leq n \\ (k,n) = 1}} \prod_{\substack{\ell \mid n \\ k \not \equiv 1 (\ell)}} f_1(\ell) \prod_{\substack{\ell \mid n \\ k \equiv 1 (\ell)}}f_2(\ell) \\ &\hspace{1in} + \frac{f_2(p) p^{a-1}}{\phi(p^a)} \frac{1}{\phi(n)} \sum_{\substack{1 \leq k \leq n \\ (k,n) = 1}} \prod_{\substack{\ell \mid n \\ k \not \equiv 1 (\ell)}} f_1(\ell) \prod_{\substack{\ell \mid n \\ k \equiv 1 (\ell)}}f_2(\ell) \\ &=\frac{1}{\phi(p^a)}\left(p^{a-1}(f_1(p)(p-2) + f_2(p))\right) \cdot F(n) = F(p^a)F(n). \end{align*} $$
This completes the proof.
4.3 Applying Zywina’s approach for the cyclicity problem
Zywina [Reference Zywina62] refined the Koblitz conjecture by improving the heuristic explanation for the constant
![]() $C^{\operatorname {\mathrm {prime}}}_E$
. In essence, he interprets the desired property of a prime of Koblitz reduction in terms of Galois representations, examines the ratio of elements with the desired property in each finite level
$C^{\operatorname {\mathrm {prime}}}_E$
. In essence, he interprets the desired property of a prime of Koblitz reduction in terms of Galois representations, examines the ratio of elements with the desired property in each finite level
![]() $G_E(m)$
, and considers the limit of that ratio as m approaches infinity. In this subsection, we apply Zywina’s approach to determine the heuristic densities of primes of cyclic reduction for E and verify their concurrence with the densities proposed by Serre and Akbal–Güloğlu.
$G_E(m)$
, and considers the limit of that ratio as m approaches infinity. In this subsection, we apply Zywina’s approach to determine the heuristic densities of primes of cyclic reduction for E and verify their concurrence with the densities proposed by Serre and Akbal–Güloğlu.
Let
![]() $E/\mathbb {Q}$
be a non-CM elliptic curve and fix a good prime
$E/\mathbb {Q}$
be a non-CM elliptic curve and fix a good prime
![]() $p \neq 2$
. We now give a criterion for p to be a prime of cyclic reduction for E.Footnote
5
Let
$p \neq 2$
. We now give a criterion for p to be a prime of cyclic reduction for E.Footnote
5
Let
![]() $\operatorname {\mathrm {Frob}}_p$
denote a Frobenius element in
$\operatorname {\mathrm {Frob}}_p$
denote a Frobenius element in
![]() $\operatorname {\mathrm {Gal}}(\overline {\mathbb {Q}}/\mathbb {Q})$
at p. By [Reference Cojocaru and Ram Murty20, Lemma 2.1], we have that
$\operatorname {\mathrm {Gal}}(\overline {\mathbb {Q}}/\mathbb {Q})$
at p. By [Reference Cojocaru and Ram Murty20, Lemma 2.1], we have that
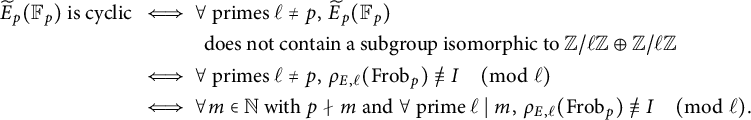 $$ \begin{align*} \widetilde{E}_p(\mathbb{F}_p) \text{ is cyclic } & \iff \forall \text{ primes } \ell \neq p, \, \widetilde{E}_p(\mathbb{F}_p)\\ &\qquad\quad \text{ does not contain a subgroup isomorphic to } \mathbb{Z}/\ell \mathbb{Z} \oplus \mathbb{Z}/\ell \mathbb{Z} \\ & \iff \forall \text{ primes } \ell \neq p, \, \rho_{E,\ell}(\operatorname{\mathrm{Frob}}_p) \not\equiv I \quad\pmod{\ell} \\ &\iff \forall m \in \mathbb{N} \text{ with } p \nmid m \text{ and } \forall \text{ prime } \ell \mid m, \, \rho_{E,\ell}(\operatorname{\mathrm{Frob}}_p) \not\equiv I \quad\pmod{\ell}. \end{align*} $$
$$ \begin{align*} \widetilde{E}_p(\mathbb{F}_p) \text{ is cyclic } & \iff \forall \text{ primes } \ell \neq p, \, \widetilde{E}_p(\mathbb{F}_p)\\ &\qquad\quad \text{ does not contain a subgroup isomorphic to } \mathbb{Z}/\ell \mathbb{Z} \oplus \mathbb{Z}/\ell \mathbb{Z} \\ & \iff \forall \text{ primes } \ell \neq p, \, \rho_{E,\ell}(\operatorname{\mathrm{Frob}}_p) \not\equiv I \quad\pmod{\ell} \\ &\iff \forall m \in \mathbb{N} \text{ with } p \nmid m \text{ and } \forall \text{ prime } \ell \mid m, \, \rho_{E,\ell}(\operatorname{\mathrm{Frob}}_p) \not\equiv I \quad\pmod{\ell}. \end{align*} $$
Drawing a parallel to (26), we consider the set
and the ratio
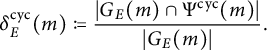
Taking the limit of
![]() $\delta ^{\operatorname {\mathrm {cyc}}}_E(m)$
over all positive integers, ordered by divisibility, we expect to obtain the heuristic density of primes of cyclic reduction.
$\delta ^{\operatorname {\mathrm {cyc}}}_E(m)$
over all positive integers, ordered by divisibility, we expect to obtain the heuristic density of primes of cyclic reduction.
Proposition 4.7 Let
![]() $E/\mathbb {Q}$
be a non-CM elliptic curve of adelic level
$E/\mathbb {Q}$
be a non-CM elliptic curve of adelic level
![]() $m_E$
. Then
$m_E$
. Then
![]() $\delta ^{\operatorname {\mathrm {cyc}}}_{E}(\cdot )$
, as an arithmetic function, satisfies the following properties:
$\delta ^{\operatorname {\mathrm {cyc}}}_{E}(\cdot )$
, as an arithmetic function, satisfies the following properties:
-
(1) for any positive integer m,
 $\delta ^{\operatorname {\mathrm {cyc}}}_E(m) = \delta ^{\operatorname {\mathrm {cyc}}}_E(\operatorname {\mathrm {rad}}(m))$
;
$\delta ^{\operatorname {\mathrm {cyc}}}_E(m) = \delta ^{\operatorname {\mathrm {cyc}}}_E(\operatorname {\mathrm {rad}}(m))$
; -
(2) for any prime
 $\ell \nmid m_E$
and integer d coprime to
$\ell \nmid m_E$
and integer d coprime to
 $\ell $
,
$\ell $
,
 $\delta ^{\operatorname {\mathrm {cyc}}}_{E}(d\ell ) = \delta ^{\operatorname {\mathrm {cyc}}}_E(d) \cdot \delta ^{\operatorname {\mathrm {cyc}}}_E(\ell )$
.
$\delta ^{\operatorname {\mathrm {cyc}}}_{E}(d\ell ) = \delta ^{\operatorname {\mathrm {cyc}}}_E(d) \cdot \delta ^{\operatorname {\mathrm {cyc}}}_E(\ell )$
.
Therefore, the heuristic density of primes of cyclic reduction can be expressed as follows,
Proof Follows similarly to the proof of Proposition 4.2.
Remark 4.8 One can easily check that for
![]() $\ell \nmid m_E$
,
$\ell \nmid m_E$
,
and hence the infinite product converges absolutely.
We now verify that the limit
![]() $\lim _{m \to \infty } \delta _E^{\operatorname {\mathrm {cyc}}}(m)$
appearing in Proposition 4.7 coincides with the cyclicity constant
$\lim _{m \to \infty } \delta _E^{\operatorname {\mathrm {cyc}}}(m)$
appearing in Proposition 4.7 coincides with the cyclicity constant
![]() $C^{\operatorname {\mathrm {cyc}}}_E$
originally defined by Serre [Reference Serre51, pp. 465–468].
$C^{\operatorname {\mathrm {cyc}}}_E$
originally defined by Serre [Reference Serre51, pp. 465–468].
Proposition 4.9 Let
![]() $E/\mathbb {Q}$
be a non-CM elliptic curve. Then we have
$E/\mathbb {Q}$
be a non-CM elliptic curve. Then we have
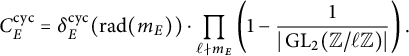 $$ \begin{align*}C^{\operatorname{\mathrm{cyc}}}_E = \delta_E^{\operatorname{\mathrm{cyc}}}(\operatorname{\mathrm{rad}}(m_E)) \cdot \prod_{\ell \nmid m_E} \left( 1 - \frac{1}{|\operatorname{\mathrm{GL}}_2(\mathbb{Z}/\ell\mathbb{Z})|}\right).\end{align*} $$
$$ \begin{align*}C^{\operatorname{\mathrm{cyc}}}_E = \delta_E^{\operatorname{\mathrm{cyc}}}(\operatorname{\mathrm{rad}}(m_E)) \cdot \prod_{\ell \nmid m_E} \left( 1 - \frac{1}{|\operatorname{\mathrm{GL}}_2(\mathbb{Z}/\ell\mathbb{Z})|}\right).\end{align*} $$
Proof Let
![]() $R = \operatorname {\mathrm {rad}}(m_E)$
. By (19) and (44), it suffices to check
$R = \operatorname {\mathrm {rad}}(m_E)$
. By (19) and (44), it suffices to check
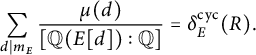 $$ \begin{align*}\sum_{d\mid m_E} \frac{\mu(d)}{[\mathbb{Q}(E[d]) : \mathbb{Q}]} = \delta^{\operatorname{\mathrm{cyc}}}_E(R).\end{align*} $$
$$ \begin{align*}\sum_{d\mid m_E} \frac{\mu(d)}{[\mathbb{Q}(E[d]) : \mathbb{Q}]} = \delta^{\operatorname{\mathrm{cyc}}}_E(R).\end{align*} $$
Let m be a positive integer and
![]() $d \mid m$
. We define
$d \mid m$
. We define
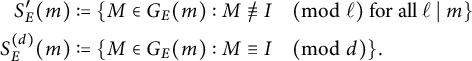
From the definition, one may observe that
![]() $G_E(R) \cap \Psi ^{\operatorname {\mathrm {cyc}}}(R) = S^{\prime }_E(R)$
. Thus, we have
$G_E(R) \cap \Psi ^{\operatorname {\mathrm {cyc}}}(R) = S^{\prime }_E(R)$
. Thus, we have
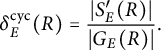 $$ \begin{align*}\delta_E^{\operatorname{\mathrm{cyc}}}(R) = \frac{|S^{\prime}_E(R)|}{|G_E(R)|}.\end{align*} $$
$$ \begin{align*}\delta_E^{\operatorname{\mathrm{cyc}}}(R) = \frac{|S^{\prime}_E(R)|}{|G_E(R)|}.\end{align*} $$
Also, note that
![]() $S_E^{(d)}(d) = \{I\}$
. Let
$S_E^{(d)}(d) = \{I\}$
. Let
![]() $\varpi \colon G_E(m) \to G_E(d)$
be the natural reduction map. Then,
$\varpi \colon G_E(m) \to G_E(d)$
be the natural reduction map. Then,
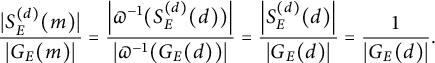 $$ \begin{align*}\frac{|S^{(d)}_E(m)|}{|G_E(m)|} = \frac{\left|\varpi^{-1}(S^{(d)}_E(d))\right|}{\left|\varpi^{-1}(G_E(d))\right|} = \frac{\left|S_E^{(d)}(d)\right|}{\left|G_E(d)\right|} = \frac{1}{|G_E(d)|}.\end{align*} $$
$$ \begin{align*}\frac{|S^{(d)}_E(m)|}{|G_E(m)|} = \frac{\left|\varpi^{-1}(S^{(d)}_E(d))\right|}{\left|\varpi^{-1}(G_E(d))\right|} = \frac{\left|S_E^{(d)}(d)\right|}{\left|G_E(d)\right|} = \frac{1}{|G_E(d)|}.\end{align*} $$
Observe that
![]() $S^{\prime }_E(R) = G_E(R) - \bigcup _{\ell \mid R} S^{(\ell )}_E(R)$
. By the principle of inclusion–exclusion, we obtain
$S^{\prime }_E(R) = G_E(R) - \bigcup _{\ell \mid R} S^{(\ell )}_E(R)$
. By the principle of inclusion–exclusion, we obtain
 $$ \begin{align*}\delta_E^{\operatorname{\mathrm{cyc}}}(R) = \frac{|S^{\prime}_E(R)|}{|G_E(R)|} = \sum_{d \mid R} \frac{\mu(d)}{|G_E(d)|} = \sum_{d\mid m_E} \frac{\mu(d)}{[\mathbb{Q}(E[d]):\mathbb{Q}]}.\end{align*} $$
$$ \begin{align*}\delta_E^{\operatorname{\mathrm{cyc}}}(R) = \frac{|S^{\prime}_E(R)|}{|G_E(R)|} = \sum_{d \mid R} \frac{\mu(d)}{|G_E(d)|} = \sum_{d\mid m_E} \frac{\mu(d)}{[\mathbb{Q}(E[d]):\mathbb{Q}]}.\end{align*} $$
This completes the proof.
Now, we construct a heuristic density of primes of cyclic reduction that lie in an arithmetic progression. Consider
We define
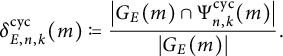
Drawing parallels from Zywina/s approach, we consider the limit
where the limit is taken over all positive integers, ordered by divisibility. We’ll prove in Proposition 4.12 that (45) coincides with
![]() $C_{E,n,k}^{\operatorname {\mathrm {cyc}}}$
as defined in [Reference Akbal and Güloğlu1]. To do so, we’ll first give some properties of
$C_{E,n,k}^{\operatorname {\mathrm {cyc}}}$
as defined in [Reference Akbal and Güloğlu1]. To do so, we’ll first give some properties of
![]() $\delta _{E,n,k}^{\operatorname {\mathrm {cyc}}}(\cdot )$
.
$\delta _{E,n,k}^{\operatorname {\mathrm {cyc}}}(\cdot )$
.
Proposition 4.10 Let
![]() $E/\mathbb {Q}$
be a non-CM elliptic curve of adelic level
$E/\mathbb {Q}$
be a non-CM elliptic curve of adelic level
![]() $m_E$
. Fix a positive integer n. Set L as in (7). Then,
$m_E$
. Fix a positive integer n. Set L as in (7). Then,
![]() $\delta _{E,n,k}^{\operatorname {\mathrm {cyc}}}(\cdot )$
, as an arithmetic function, satisfies the following properties:
$\delta _{E,n,k}^{\operatorname {\mathrm {cyc}}}(\cdot )$
, as an arithmetic function, satisfies the following properties:
-
(1) Let
 $L \mid L^{\prime } \mid L^\infty $
. Then,
$L \mid L^{\prime } \mid L^\infty $
. Then,
 $\delta _{E,n,k}^{\operatorname {\mathrm {cyc}}}(L) = \delta _{E,n,k}^{\operatorname {\mathrm {cyc}}}(L^{\prime })$
;
$\delta _{E,n,k}^{\operatorname {\mathrm {cyc}}}(L) = \delta _{E,n,k}^{\operatorname {\mathrm {cyc}}}(L^{\prime })$
; -
(2) Let
 $\ell ^\alpha $
be a prime power and d be a positive integer with
$\ell ^\alpha $
be a prime power and d be a positive integer with
 $(\ell , Ld) = 1$
. Then,
$(\ell , Ld) = 1$
. Then,
 $\delta _{E,n,k}^{\operatorname {\mathrm {cyc}}}(d\ell ^a) = \delta _{E,n,k}^{\operatorname {\mathrm {cyc}}}(d) \cdot \delta _{E,n,k}^{\operatorname {\mathrm {cyc}}}(\ell ^\alpha )$
.
$\delta _{E,n,k}^{\operatorname {\mathrm {cyc}}}(d\ell ^a) = \delta _{E,n,k}^{\operatorname {\mathrm {cyc}}}(d) \cdot \delta _{E,n,k}^{\operatorname {\mathrm {cyc}}}(\ell ^\alpha )$
. -
(3) Let
 $\ell ^\alpha \parallel n$
and
$\ell ^\alpha \parallel n$
and
 $(\ell , L) = 1$
. Then, for any
$(\ell , L) = 1$
. Then, for any
 $\beta> \alpha $
,
$\beta> \alpha $
,
 $\delta ^{\operatorname {\mathrm {cyc}}}_{E,n,k}(\ell ^\beta ) = \delta ^{\operatorname {\mathrm {cyc}}}_{E,n,k}(\ell ^\alpha )$
. Further, if
$\delta ^{\operatorname {\mathrm {cyc}}}_{E,n,k}(\ell ^\beta ) = \delta ^{\operatorname {\mathrm {cyc}}}_{E,n,k}(\ell ^\alpha )$
. Further, if
 $\ell \nmid nL$
, we have
$\ell \nmid nL$
, we have
 $\delta _{E,n,k}^{\operatorname {\mathrm {cyc}}}(\ell ^\beta ) = \delta ^{\operatorname {\mathrm {cyc}}}_E(\ell )$
.
$\delta _{E,n,k}^{\operatorname {\mathrm {cyc}}}(\ell ^\beta ) = \delta ^{\operatorname {\mathrm {cyc}}}_E(\ell )$
.
Therefore, (45) can be expressed as follows,
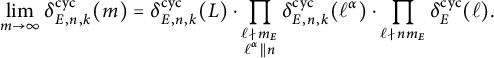
and the product converges absolutely.
Proof One can argue similarly to the proof of Proposition 4.4 to obtain the desired results. The absolute convergence of (46) follows from Remark 4.8.
The next lemma allows us to describe (46) explicitly.
Lemma 4.11 Let
![]() $E/\mathbb {Q}$
be a non-CM elliptic curve of adelic level
$E/\mathbb {Q}$
be a non-CM elliptic curve of adelic level
![]() $m_E$
. Suppose
$m_E$
. Suppose
![]() $\ell ^a \parallel n$
and
$\ell ^a \parallel n$
and
![]() $\ell \nmid m_E$
. For any k coprime to n, we have
$\ell \nmid m_E$
. For any k coprime to n, we have
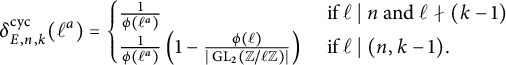 $$ \begin{align*}\delta^{\operatorname{\mathrm{cyc}}}_{E,n,k}(\ell^a) = \begin{cases} \frac{1}{\phi(\ell^a)} & \text{ if } \ell \mid n \text{ and } \ell \nmid (k-1) \\ \frac{1}{\phi(\ell^a)}\left ( 1 - \frac{\phi(\ell)}{|\operatorname{\mathrm{GL}}_2(\mathbb{Z}/\ell\mathbb{Z})|}\right) & \text{ if } \ell \mid (n,k-1). \end{cases}\end{align*} $$
$$ \begin{align*}\delta^{\operatorname{\mathrm{cyc}}}_{E,n,k}(\ell^a) = \begin{cases} \frac{1}{\phi(\ell^a)} & \text{ if } \ell \mid n \text{ and } \ell \nmid (k-1) \\ \frac{1}{\phi(\ell^a)}\left ( 1 - \frac{\phi(\ell)}{|\operatorname{\mathrm{GL}}_2(\mathbb{Z}/\ell\mathbb{Z})|}\right) & \text{ if } \ell \mid (n,k-1). \end{cases}\end{align*} $$
Proof Since
![]() $\ell \nmid m_E$
, we have
$\ell \nmid m_E$
, we have
![]() $G_E(\ell ^a) \simeq \operatorname {\mathrm {GL}}_2(\mathbb {Z}/\ell ^a\mathbb {Z})$
, and hence
$G_E(\ell ^a) \simeq \operatorname {\mathrm {GL}}_2(\mathbb {Z}/\ell ^a\mathbb {Z})$
, and hence
![]() $|G_E(\ell ^a)| = (\ell ^2-1)(\ell ^2-\ell )\ell ^{4(a-1)}$
. Applying Corollary 3.2, we obtain the desired results.
$|G_E(\ell ^a)| = (\ell ^2-1)(\ell ^2-\ell )\ell ^{4(a-1)}$
. Applying Corollary 3.2, we obtain the desired results.
Let
![]() $E/\mathbb {Q}$
be a non-CM elliptic curve of adelic level
$E/\mathbb {Q}$
be a non-CM elliptic curve of adelic level
![]() $m_E$
. Let
$m_E$
. Let
![]() $n = n_1n_2$
where
$n = n_1n_2$
where
![]() $n_1 = \gcd (n,m_E^\infty )$
and
$n_1 = \gcd (n,m_E^\infty )$
and
![]() $(n_2,m_E) = 1$
. By (44), (46), and Lemma 4.11, we obtain
$(n_2,m_E) = 1$
. By (44), (46), and Lemma 4.11, we obtain
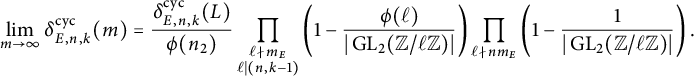 $$ \begin{align} \lim_{m\to \infty} \delta^{\operatorname{\mathrm{cyc}}}_{E,n,k}(m) = \frac{\delta_{E,n,k}^{\operatorname{\mathrm{cyc}}}(L)}{\phi(n_2)} \prod_{\substack{\ell \nmid m_E \\ \ell \mid (n,k-1)}}\left( 1- \frac{\phi(\ell)}{|\operatorname{\mathrm{GL}}_2(\mathbb{Z}/\ell\mathbb{Z})|}\right) \prod_{\ell \nmid nm_E} \left( 1 - \frac{1}{|\operatorname{\mathrm{GL}}_2(\mathbb{Z}/\ell\mathbb{Z})|}\right). \end{align} $$
$$ \begin{align} \lim_{m\to \infty} \delta^{\operatorname{\mathrm{cyc}}}_{E,n,k}(m) = \frac{\delta_{E,n,k}^{\operatorname{\mathrm{cyc}}}(L)}{\phi(n_2)} \prod_{\substack{\ell \nmid m_E \\ \ell \mid (n,k-1)}}\left( 1- \frac{\phi(\ell)}{|\operatorname{\mathrm{GL}}_2(\mathbb{Z}/\ell\mathbb{Z})|}\right) \prod_{\ell \nmid nm_E} \left( 1 - \frac{1}{|\operatorname{\mathrm{GL}}_2(\mathbb{Z}/\ell\mathbb{Z})|}\right). \end{align} $$
We now prove that (47) equals the cyclicity constant proposed by Akbal and Gülğlu.
Proposition 4.12 Let
![]() $E/\mathbb {Q}$
be a non-CM elliptic curve of adelic level
$E/\mathbb {Q}$
be a non-CM elliptic curve of adelic level
![]() $m_E$
and n be a positive integer. Let
$m_E$
and n be a positive integer. Let
![]() $n = n_1n_2$
where
$n = n_1n_2$
where
![]() $n_1 = \gcd (n,m_E^\infty )$
and
$n_1 = \gcd (n,m_E^\infty )$
and
![]() $(n_2,m_E) = 1$
. Then we have
$(n_2,m_E) = 1$
. Then we have
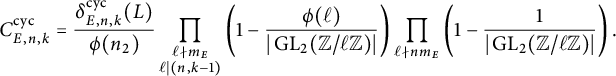 $$ \begin{align*} C^{\operatorname{\mathrm{cyc}}}_{E,n,k} = \frac{\delta_{E,n,k}^{\operatorname{\mathrm{cyc}}}(L)}{\phi(n_2)} \prod_{\substack{\ell \nmid m_E \\ \ell \mid (n,k-1)}}\left( 1- \frac{\phi(\ell)}{|\operatorname{\mathrm{GL}}_2(\mathbb{Z}/\ell\mathbb{Z})|}\right) \prod_{\ell \nmid nm_E} \left( 1 - \frac{1}{|\operatorname{\mathrm{GL}}_2(\mathbb{Z}/\ell\mathbb{Z})|}\right). \end{align*} $$
$$ \begin{align*} C^{\operatorname{\mathrm{cyc}}}_{E,n,k} = \frac{\delta_{E,n,k}^{\operatorname{\mathrm{cyc}}}(L)}{\phi(n_2)} \prod_{\substack{\ell \nmid m_E \\ \ell \mid (n,k-1)}}\left( 1- \frac{\phi(\ell)}{|\operatorname{\mathrm{GL}}_2(\mathbb{Z}/\ell\mathbb{Z})|}\right) \prod_{\ell \nmid nm_E} \left( 1 - \frac{1}{|\operatorname{\mathrm{GL}}_2(\mathbb{Z}/\ell\mathbb{Z})|}\right). \end{align*} $$
Proof Define
Let
![]() $R = \operatorname {\mathrm {rad}}(m_E)$
. By [Reference Jones and Lee33, p. 13], (22) can be expressed as follows,
$R = \operatorname {\mathrm {rad}}(m_E)$
. By [Reference Jones and Lee33, p. 13], (22) can be expressed as follows,
 $$ \begin{align} \frac{|S^{\prime}_{E,n,k}(R)|}{|\operatorname{\mathrm{Gal}}(\mathbb{Q}(E[R]) \mathbb{Q}(\zeta_n)/\mathbb{Q})|} \prod_{\substack{\ell \nmid m_E \\ \ell (n,k-1)}} \left(1-\frac{\phi(\ell)}{|\operatorname{\mathrm{GL}}_2(\mathbb{Z}/\ell\mathbb{Z})|}\right) \prod_{\ell \nmid nm_E} \left(1-\frac{1}{|\operatorname{\mathrm{GL}}_2(\mathbb{Z}/\ell\mathbb{Z})|}\right). \end{align} $$
$$ \begin{align} \frac{|S^{\prime}_{E,n,k}(R)|}{|\operatorname{\mathrm{Gal}}(\mathbb{Q}(E[R]) \mathbb{Q}(\zeta_n)/\mathbb{Q})|} \prod_{\substack{\ell \nmid m_E \\ \ell (n,k-1)}} \left(1-\frac{\phi(\ell)}{|\operatorname{\mathrm{GL}}_2(\mathbb{Z}/\ell\mathbb{Z})|}\right) \prod_{\ell \nmid nm_E} \left(1-\frac{1}{|\operatorname{\mathrm{GL}}_2(\mathbb{Z}/\ell\mathbb{Z})|}\right). \end{align} $$
Thus, it suffices to verify that
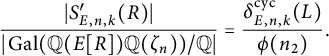 $$ \begin{align*}\frac{|S^{\prime}_{E,n,k}(R)|}{|\operatorname{\mathrm{Gal}}(\mathbb{Q}(E[R])\mathbb{Q}(\zeta_n))/\mathbb{Q}|} = \frac{\delta_{E,n,k}^{\operatorname{\mathrm{cyc}}}(L)}{\phi(n_2)}.\end{align*} $$
$$ \begin{align*}\frac{|S^{\prime}_{E,n,k}(R)|}{|\operatorname{\mathrm{Gal}}(\mathbb{Q}(E[R])\mathbb{Q}(\zeta_n))/\mathbb{Q}|} = \frac{\delta_{E,n,k}^{\operatorname{\mathrm{cyc}}}(L)}{\phi(n_2)}.\end{align*} $$
By the Weil pairing, we have
![]() $\mathbb {Q}(\zeta _{n_2}) \subseteq \mathbb {Q}(E[n_2])$
. Thus, we see that
$\mathbb {Q}(\zeta _{n_2}) \subseteq \mathbb {Q}(E[n_2])$
. Thus, we see that
![]() $\mathbb {Q}(E[R])\mathbb {Q}(\zeta _{n_1})$
and
$\mathbb {Q}(E[R])\mathbb {Q}(\zeta _{n_1})$
and
![]() $\mathbb {Q}(\zeta _{n_2})$
must be linearly disjoint by Lemma 2.2, and hence
$\mathbb {Q}(\zeta _{n_2})$
must be linearly disjoint by Lemma 2.2, and hence
Under the isomorphism, the set
![]() $S^{\prime }_{E,n,k}(R)$
can be identified as
$S^{\prime }_{E,n,k}(R)$
can be identified as
![]() $S^{\prime }_{E,n_1,k}(R) \times \left \{\sigma _k\right \}$
, and hence
$S^{\prime }_{E,n_1,k}(R) \times \left \{\sigma _k\right \}$
, and hence
![]() $|S^{\prime }_{E,n,k}(R)| = |S^{\prime }_{E,n_1,k}(R)|$
. Thus, we have
$|S^{\prime }_{E,n,k}(R)| = |S^{\prime }_{E,n_1,k}(R)|$
. Thus, we have
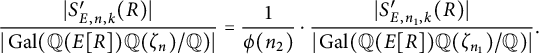 $$ \begin{align*}\frac{|S^{\prime}_{E,n,k}(R)|}{|\operatorname{\mathrm{Gal}}(\mathbb{Q}(E[R])\mathbb{Q}(\zeta_n)/\mathbb{Q})|} = \frac{1}{\phi(n_2)} \cdot \frac{|S^{\prime}_{E,n_1,k}(R)|}{|\operatorname{\mathrm{Gal}}(\mathbb{Q}(E[R])\mathbb{Q}(\zeta_{n_1})/\mathbb{Q})|}.\end{align*} $$
$$ \begin{align*}\frac{|S^{\prime}_{E,n,k}(R)|}{|\operatorname{\mathrm{Gal}}(\mathbb{Q}(E[R])\mathbb{Q}(\zeta_n)/\mathbb{Q})|} = \frac{1}{\phi(n_2)} \cdot \frac{|S^{\prime}_{E,n_1,k}(R)|}{|\operatorname{\mathrm{Gal}}(\mathbb{Q}(E[R])\mathbb{Q}(\zeta_{n_1})/\mathbb{Q})|}.\end{align*} $$
Remark that
![]() $\mathbb {Q}(E[R]) \subseteq \mathbb {Q}(E[L])$
and
$\mathbb {Q}(E[R]) \subseteq \mathbb {Q}(E[L])$
and
![]() $\mathbb {Q}(\zeta _{n_1}) \subseteq \mathbb {Q}(E[L])$
by the definition of L. Thus, the usual restriction
$\mathbb {Q}(\zeta _{n_1}) \subseteq \mathbb {Q}(E[L])$
by the definition of L. Thus, the usual restriction
![]() $\varpi \colon G_E(L) \to \operatorname {\mathrm {Gal}}(\mathbb {Q}(E[R])\mathbb {Q}(\zeta _{n_1})/\mathbb {Q})$
gives a surjective group homomorphism.
$\varpi \colon G_E(L) \to \operatorname {\mathrm {Gal}}(\mathbb {Q}(E[R])\mathbb {Q}(\zeta _{n_1})/\mathbb {Q})$
gives a surjective group homomorphism.
Viewing
![]() $G_E(L)$
as a subgroup of
$G_E(L)$
as a subgroup of
![]() $\operatorname {\mathrm {GL}}_2(\mathbb {Z}/L\mathbb {Z})$
, we may observe that
$\operatorname {\mathrm {GL}}_2(\mathbb {Z}/L\mathbb {Z})$
, we may observe that
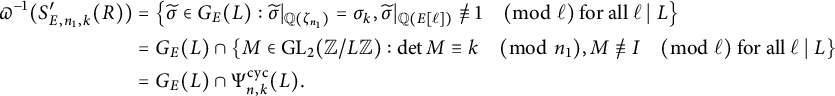 $$ \begin{align*} \varpi^{-1}(S^{\prime}_{E,n_1,k}(R)) &= \left\{\widetilde{\sigma} \in G_E(L) : \widetilde{\sigma}|_{\mathbb{Q}(\zeta_{n_1})} = \sigma_{k}, \widetilde{\sigma}|_{\mathbb{Q}(E[\ell])} \not \equiv 1 \quad\pmod {\ell} \text{ for all } \ell \mid L \right\} \\ &= G_E(L) \cap \left\{M \in \operatorname{\mathrm{GL}}_2(\mathbb{Z}/L\mathbb{Z}) : \operatorname{det} M \equiv k \quad\pmod {n_1}, M \not \equiv I \quad\pmod {\ell} \text{ for all } \ell \mid L \right\} \\ &= G_E(L) \cap \Psi^{\operatorname{\mathrm{cyc}}}_{n,k}(L). \end{align*} $$
$$ \begin{align*} \varpi^{-1}(S^{\prime}_{E,n_1,k}(R)) &= \left\{\widetilde{\sigma} \in G_E(L) : \widetilde{\sigma}|_{\mathbb{Q}(\zeta_{n_1})} = \sigma_{k}, \widetilde{\sigma}|_{\mathbb{Q}(E[\ell])} \not \equiv 1 \quad\pmod {\ell} \text{ for all } \ell \mid L \right\} \\ &= G_E(L) \cap \left\{M \in \operatorname{\mathrm{GL}}_2(\mathbb{Z}/L\mathbb{Z}) : \operatorname{det} M \equiv k \quad\pmod {n_1}, M \not \equiv I \quad\pmod {\ell} \text{ for all } \ell \mid L \right\} \\ &= G_E(L) \cap \Psi^{\operatorname{\mathrm{cyc}}}_{n,k}(L). \end{align*} $$
Therefore,
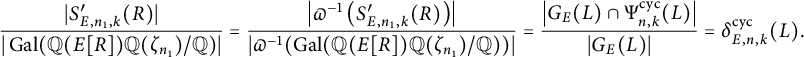 $$ \begin{align*}\frac{|S^{\prime}_{E,n_1,k}(R)|}{|\operatorname{\mathrm{Gal}}(\mathbb{Q}(E[R])\mathbb{Q}(\zeta_{n_1})/\mathbb{Q})|} = \frac{\left|\varpi^{-1}\left(S^{\prime}_{E,n_1,k}(R)\right)\right|}{\left|\varpi^{-1}(\operatorname{\mathrm{Gal}}(\mathbb{Q}(E[R])\mathbb{Q}(\zeta_{n_1})/\mathbb{Q}))\right|} = \frac{\left| G_E(L)\cap \Psi^{\operatorname{\mathrm{cyc}}}_{n,k}(L)\right|}{\left|G_E(L)\right|} = \delta^{\operatorname{\mathrm{cyc}}}_{E,n,k}(L).\end{align*} $$
$$ \begin{align*}\frac{|S^{\prime}_{E,n_1,k}(R)|}{|\operatorname{\mathrm{Gal}}(\mathbb{Q}(E[R])\mathbb{Q}(\zeta_{n_1})/\mathbb{Q})|} = \frac{\left|\varpi^{-1}\left(S^{\prime}_{E,n_1,k}(R)\right)\right|}{\left|\varpi^{-1}(\operatorname{\mathrm{Gal}}(\mathbb{Q}(E[R])\mathbb{Q}(\zeta_{n_1})/\mathbb{Q}))\right|} = \frac{\left| G_E(L)\cap \Psi^{\operatorname{\mathrm{cyc}}}_{n,k}(L)\right|}{\left|G_E(L)\right|} = \delta^{\operatorname{\mathrm{cyc}}}_{E,n,k}(L).\end{align*} $$
This completes the proof.
Remark 4.13 As one may have observed from Conjectures 1.1 and 1.3, the conjectural growth rates of
![]() $\pi _E^{\operatorname {\mathrm {cyc}}}(x)$
and
$\pi _E^{\operatorname {\mathrm {cyc}}}(x)$
and
![]() $\pi _E^{\operatorname {\mathrm {prime}}}(x)$
are different. Thus, there is an intrinsic difference between
$\pi _E^{\operatorname {\mathrm {prime}}}(x)$
are different. Thus, there is an intrinsic difference between
![]() $C^{\operatorname {\mathrm {cyc}}}_E$
and
$C^{\operatorname {\mathrm {cyc}}}_E$
and
![]() $C^{\operatorname {\mathrm {prime}}}_E$
. In particular,
$C^{\operatorname {\mathrm {prime}}}_E$
. In particular,
![]() $C^{\operatorname {\mathrm {cyc}}}_E$
can be interpreted as the (conjectural) density of primes of cyclic reduction for E whereas
$C^{\operatorname {\mathrm {cyc}}}_E$
can be interpreted as the (conjectural) density of primes of cyclic reduction for E whereas
![]() $C^{\operatorname {\mathrm {prime}}}_E$
should not be interpreted analogously. A similar remark holds for
$C^{\operatorname {\mathrm {prime}}}_E$
should not be interpreted analogously. A similar remark holds for
![]() $\pi _E^{\operatorname {\mathrm {cyc}}}(x;n,k)$
and
$\pi _E^{\operatorname {\mathrm {cyc}}}(x;n,k)$
and
![]() $\pi _E^{\operatorname {\mathrm {prime}}}(x;n,k)$
and their respective constants.
$\pi _E^{\operatorname {\mathrm {prime}}}(x;n,k)$
and their respective constants.
5 On the cyclicity and Koblitz constants for Serre curves
We begin by fixing some notation that will hold throughout the section. Let
![]() $E/\mathbb {Q}$
be a Serre curve of discriminant
$E/\mathbb {Q}$
be a Serre curve of discriminant
![]() $\Delta _E$
, n be a positive integer, and k be an integer coprime to n. Let
$\Delta _E$
, n be a positive integer, and k be an integer coprime to n. Let
![]() $\Delta ^{\prime }$
be the squarefree part of
$\Delta ^{\prime }$
be the squarefree part of
![]() $\Delta _E$
. By Proposition 2.4, we have
$\Delta _E$
. By Proposition 2.4, we have
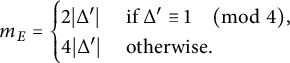 $$ \begin{align*} m_E = \begin{cases} 2|\Delta^{\prime}| & \text{ if } \Delta^{\prime} \equiv 1 \quad\pmod 4, \\ 4|\Delta^{\prime}| & \text{ otherwise}. \end{cases} \end{align*} $$
$$ \begin{align*} m_E = \begin{cases} 2|\Delta^{\prime}| & \text{ if } \Delta^{\prime} \equiv 1 \quad\pmod 4, \\ 4|\Delta^{\prime}| & \text{ otherwise}. \end{cases} \end{align*} $$
Let L be defined as in (7). The goal of this section is to develop formulas for
![]() $C_{E,n,k}^{\operatorname {\mathrm {cyc}}}$
and
$C_{E,n,k}^{\operatorname {\mathrm {cyc}}}$
and
![]() $C_{E,n,k}^{\operatorname {\mathrm {prime}}}$
with our assumption that E is a Serre curve. By Propositions 4.4 and 4.10, it suffices to compute
$C_{E,n,k}^{\operatorname {\mathrm {prime}}}$
with our assumption that E is a Serre curve. By Propositions 4.4 and 4.10, it suffices to compute
![]() $\delta _{E,n,k}^{\operatorname {\mathrm {cyc}}}(L)$
and
$\delta _{E,n,k}^{\operatorname {\mathrm {cyc}}}(L)$
and
![]() $\delta _{E,n,k}^{\operatorname {\mathrm {prime}}}(L)$
.
$\delta _{E,n,k}^{\operatorname {\mathrm {prime}}}(L)$
.
For an integer n, we set
![]() $n = n_1n_2$
where
$n = n_1n_2$
where
![]() $n_1 = (n,m_E^\infty )$
and
$n_1 = (n,m_E^\infty )$
and
![]() $(n_2,m_E) = 1$
. There are two cases to consider:
$(n_2,m_E) = 1$
. There are two cases to consider:
![]() $m_E \nmid L$
and
$m_E \nmid L$
and
![]() $m_E \mid L$
. The former occurs if and only if one of the following holds:
$m_E \mid L$
. The former occurs if and only if one of the following holds:
-
•
 $\Delta ^{\prime } \equiv 3 \ \pmod 4$
and
$\Delta ^{\prime } \equiv 3 \ \pmod 4$
and
 $2 \nmid n$
;
$2 \nmid n$
; -
•
 $\Delta ^{\prime } \equiv 2 \ \pmod 4$
and
$\Delta ^{\prime } \equiv 2 \ \pmod 4$
and
 $4 \nmid n$
.
$4 \nmid n$
.
We write
![]() $L = 2^{\alpha } \cdot L^{\operatorname {\mathrm {odd}}}$
where
$L = 2^{\alpha } \cdot L^{\operatorname {\mathrm {odd}}}$
where
![]() $L^{\operatorname {\mathrm {odd}}}$
is an odd integer; observe that
$L^{\operatorname {\mathrm {odd}}}$
is an odd integer; observe that
![]() $|\Delta ^{\prime }|$
divides
$|\Delta ^{\prime }|$
divides
![]() $L^{\operatorname {\mathrm {odd}}}$
. We now define two sign functions that depend on
$L^{\operatorname {\mathrm {odd}}}$
. We now define two sign functions that depend on
![]() $\Delta ^{\prime }, k$
and appear in Theorem 1.7.
$\Delta ^{\prime }, k$
and appear in Theorem 1.7.
Definition 5.1 Let
![]() $E/\mathbb {Q}$
be a Serre curve of discriminant
$E/\mathbb {Q}$
be a Serre curve of discriminant
![]() $\Delta _E$
. Let
$\Delta _E$
. Let
![]() $\Delta ^{\prime }$
and k defined as above. Assume
$\Delta ^{\prime }$
and k defined as above. Assume
![]() $m_E\mid L$
. We define
$m_E\mid L$
. We define
![]() $\tau = \tau (\Delta ^{\prime },k)$
as follows.
$\tau = \tau (\Delta ^{\prime },k)$
as follows.
-
• If
 $\Delta ^{\prime } \equiv 1 \ \pmod 4$
, we define
$\Delta ^{\prime } \equiv 1 \ \pmod 4$
, we define
 $\tau = -1$
.
$\tau = -1$
. -
• If
 $\Delta ^{\prime } \equiv 3 \ \pmod 4$
, then
$\Delta ^{\prime } \equiv 3 \ \pmod 4$
, then
 $4 \mid n$
. We define
$4 \mid n$
. We define  $$ \begin{align*}\tau = \begin{cases} -1 & \text{ if } k \equiv 1 \quad\pmod 4,\\ 1 & \text{ if } k \equiv 3 \quad\pmod 4. \end{cases}\end{align*} $$
$$ \begin{align*}\tau = \begin{cases} -1 & \text{ if } k \equiv 1 \quad\pmod 4,\\ 1 & \text{ if } k \equiv 3 \quad\pmod 4. \end{cases}\end{align*} $$
-
• If
 $\Delta ^{\prime } \equiv 2 \ \pmod 8$
, then
$\Delta ^{\prime } \equiv 2 \ \pmod 8$
, then
 $8 \mid n$
. We define
$8 \mid n$
. We define  $$ \begin{align*}\tau = \begin{cases} -1 & \text{ if } k \equiv 1,7 \quad\pmod 8, \\ 1 & \text{ if } k \equiv 3 ,5 \quad\pmod 8. \end{cases}\end{align*} $$
$$ \begin{align*}\tau = \begin{cases} -1 & \text{ if } k \equiv 1,7 \quad\pmod 8, \\ 1 & \text{ if } k \equiv 3 ,5 \quad\pmod 8. \end{cases}\end{align*} $$
-
• If
 $\Delta ^{\prime } \equiv 6 \ \pmod 8$
, then
$\Delta ^{\prime } \equiv 6 \ \pmod 8$
, then
 $8 \mid n$
. We define
$8 \mid n$
. We define  $$ \begin{align*}\tau = \begin{cases} -1 & \text{ if } k \equiv 1, 3\quad\pmod 8, \\ 1 & \text{ if } k \equiv 5,7 \quad\pmod 8. \end{cases}\end{align*} $$
$$ \begin{align*}\tau = \begin{cases} -1 & \text{ if } k \equiv 1, 3\quad\pmod 8, \\ 1 & \text{ if } k \equiv 5,7 \quad\pmod 8. \end{cases}\end{align*} $$
Finally, we define ![]() as follows,
as follows,
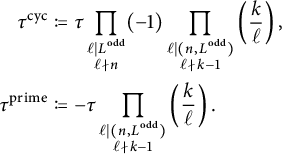
Having defined
![]() $\tau ^{\operatorname {\mathrm {cyc}}}$
and
$\tau ^{\operatorname {\mathrm {cyc}}}$
and
![]() $\tau ^{\operatorname {\mathrm {prime}}}$
, the rest of the section is devoted to proving Theorem 1.7. First, suppose
$\tau ^{\operatorname {\mathrm {prime}}}$
, the rest of the section is devoted to proving Theorem 1.7. First, suppose
![]() $m_E \nmid L$
. Then, by Proposition 2.4, we have
$m_E \nmid L$
. Then, by Proposition 2.4, we have
![]() $G_E(L) \simeq \operatorname {\mathrm {GL}}_2(\mathbb {Z}/L\mathbb {Z}) \simeq \prod _{\ell ^{\alpha } \parallel L} \operatorname {\mathrm {GL}}_2(\mathbb {Z}/\ell ^{\alpha }\mathbb {Z})$
. One can check that the isomorphism induces bijections between the sets,
$G_E(L) \simeq \operatorname {\mathrm {GL}}_2(\mathbb {Z}/L\mathbb {Z}) \simeq \prod _{\ell ^{\alpha } \parallel L} \operatorname {\mathrm {GL}}_2(\mathbb {Z}/\ell ^{\alpha }\mathbb {Z})$
. One can check that the isomorphism induces bijections between the sets,
for
![]() $\mathcal {X} \in \{\operatorname {\mathrm {cyc}},\operatorname {\mathrm {prime}}\}$
. Let
$\mathcal {X} \in \{\operatorname {\mathrm {cyc}},\operatorname {\mathrm {prime}}\}$
. Let
![]() $\ell $
be a prime factor of L. If
$\ell $
be a prime factor of L. If
![]() $\ell \nmid n$
, then we have
$\ell \nmid n$
, then we have
![]() $\alpha = 1$
by (7). The condition
$\alpha = 1$
by (7). The condition
![]() $\operatorname {det} M \equiv k \ \pmod {\gcd (n,\ell )}$
becomes trivial, and hence we have
$\operatorname {det} M \equiv k \ \pmod {\gcd (n,\ell )}$
becomes trivial, and hence we have
for
![]() $\mathcal {X} \in \{\operatorname {\mathrm {cyc}},\operatorname {\mathrm {prime}}\}$
.
$\mathcal {X} \in \{\operatorname {\mathrm {cyc}},\operatorname {\mathrm {prime}}\}$
.
On the other hand, suppose
![]() $\ell ^\alpha \parallel n$
. We have already determined the size of
$\ell ^\alpha \parallel n$
. We have already determined the size of
![]() $\Psi ^{\mathcal {X}}_{n,k}(\ell ^\alpha )$
in Corollaries 3.2 and 3.4. Based on those counts, we obtain the following.
$\Psi ^{\mathcal {X}}_{n,k}(\ell ^\alpha )$
in Corollaries 3.2 and 3.4. Based on those counts, we obtain the following.
Lemma 5.2 We have
-
(1)
 $\displaystyle \Psi _{n, k}^{\operatorname {\mathrm {cyc}}}(L)=\prod _{\substack {\ell \mid L\\\ell \nmid n}}\left ((\ell ^2-1)(\ell ^2-\ell )-1 \right ) \prod _{\substack {\ell ^{\alpha }\parallel (L, n)\\ \ell \mid k-1}}\left (\ell ^{3(\alpha -1)}(\ell ^3-\ell -1) \right ) \prod _{\substack {\ell ^{\alpha }\parallel (L, n)\\ \ell \nmid k-1}}\left (\ell ^{3(\alpha -1)}(\ell ^3-\ell ) \right )$
.
$\displaystyle \Psi _{n, k}^{\operatorname {\mathrm {cyc}}}(L)=\prod _{\substack {\ell \mid L\\\ell \nmid n}}\left ((\ell ^2-1)(\ell ^2-\ell )-1 \right ) \prod _{\substack {\ell ^{\alpha }\parallel (L, n)\\ \ell \mid k-1}}\left (\ell ^{3(\alpha -1)}(\ell ^3-\ell -1) \right ) \prod _{\substack {\ell ^{\alpha }\parallel (L, n)\\ \ell \nmid k-1}}\left (\ell ^{3(\alpha -1)}(\ell ^3-\ell ) \right )$
. -
(2)
 $\displaystyle \Psi _{n, k}^{\operatorname {\mathrm {prime}}}(L)=\prod _{\substack {\ell \mid L\\\ell \nmid n}}\left (\ell (\ell ^3-2\ell ^2-\ell +3)\right ) \prod _{\substack {\ell ^{\alpha }\parallel (L, n)\\ \ell \mid k-1}}\left (\ell ^{3(\alpha -1)}(\ell ^3-\ell ^2-\ell ) \right )\prod _{\substack {\ell ^{\alpha }\parallel (L, n)\\ \ell \nmid k-1}}\left (\ell ^{3(\alpha -1)}(\ell ^3-\ell ^2-2\ell ) \right )$
.
$\displaystyle \Psi _{n, k}^{\operatorname {\mathrm {prime}}}(L)=\prod _{\substack {\ell \mid L\\\ell \nmid n}}\left (\ell (\ell ^3-2\ell ^2-\ell +3)\right ) \prod _{\substack {\ell ^{\alpha }\parallel (L, n)\\ \ell \mid k-1}}\left (\ell ^{3(\alpha -1)}(\ell ^3-\ell ^2-\ell ) \right )\prod _{\substack {\ell ^{\alpha }\parallel (L, n)\\ \ell \nmid k-1}}\left (\ell ^{3(\alpha -1)}(\ell ^3-\ell ^2-2\ell ) \right )$
.
Based on Lemma 5.2.(1), we obtain
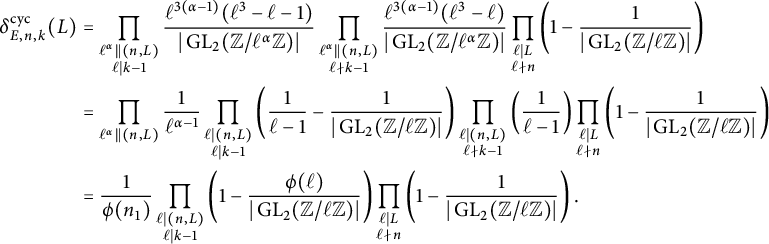 $$ \begin{align} \delta_{E,n,k}^{\operatorname{\mathrm{cyc}}}(L) &= \prod_{\substack{\ell^{\alpha} \parallel (n,L) \\ \ell\mid k-1 }} \frac{\ell^{3(\alpha-1)} (\ell^3-\ell-1)}{|\operatorname{\mathrm{GL}}_2(\mathbb{Z}/\ell^{\alpha}\mathbb{Z})|} \prod_{\substack{\ell^{\alpha} \parallel (n,L) \\ \ell\nmid k-1 }} \frac{\ell^{3(\alpha-1)}(\ell^3-\ell)}{|\operatorname{\mathrm{GL}}_2(\mathbb{Z}/\ell^{\alpha}\mathbb{Z})|} \prod_{\substack{\ell \mid L \\ \ell \nmid n}} \left( 1 - \frac{1}{|\operatorname{\mathrm{GL}}_2(\mathbb{Z}/\ell\mathbb{Z})|}\right) \nonumber\\ &= \prod_{\ell^{\alpha}\parallel (n,L)} \frac{1}{\ell^{\alpha-1}} \prod_{\substack{\ell \mid (n,L) \\ \ell\mid k-1 }}\left( \frac{1}{\ell-1} - \frac{1}{|\operatorname{\mathrm{GL}}_2(\mathbb{Z}/\ell\mathbb{Z})|}\right) \prod_{\substack{\ell \mid (n,L) \\ \ell\nmid k-1}} \left(\frac{1}{\ell-1}\right) \prod_{\substack{\ell \mid L \\ \ell \nmid n}} \left( 1 - \frac{1}{|\operatorname{\mathrm{GL}}_2(\mathbb{Z}/\ell\mathbb{Z})|}\right) \\ &= \frac{1}{\phi(n_1)} \prod_{\substack{\ell \mid (n,L) \\ \ell \mid k-1}}\left(1-\frac{\phi(\ell)}{|\operatorname{\mathrm{GL}}_2(\mathbb{Z}/\ell\mathbb{Z})|}\right) \prod_{\substack{\ell \mid L \\ \ell \nmid n}} \left( 1 - \frac{1}{|\operatorname{\mathrm{GL}}_2(\mathbb{Z}/\ell\mathbb{Z})|}\right).\nonumber \end{align} $$
$$ \begin{align} \delta_{E,n,k}^{\operatorname{\mathrm{cyc}}}(L) &= \prod_{\substack{\ell^{\alpha} \parallel (n,L) \\ \ell\mid k-1 }} \frac{\ell^{3(\alpha-1)} (\ell^3-\ell-1)}{|\operatorname{\mathrm{GL}}_2(\mathbb{Z}/\ell^{\alpha}\mathbb{Z})|} \prod_{\substack{\ell^{\alpha} \parallel (n,L) \\ \ell\nmid k-1 }} \frac{\ell^{3(\alpha-1)}(\ell^3-\ell)}{|\operatorname{\mathrm{GL}}_2(\mathbb{Z}/\ell^{\alpha}\mathbb{Z})|} \prod_{\substack{\ell \mid L \\ \ell \nmid n}} \left( 1 - \frac{1}{|\operatorname{\mathrm{GL}}_2(\mathbb{Z}/\ell\mathbb{Z})|}\right) \nonumber\\ &= \prod_{\ell^{\alpha}\parallel (n,L)} \frac{1}{\ell^{\alpha-1}} \prod_{\substack{\ell \mid (n,L) \\ \ell\mid k-1 }}\left( \frac{1}{\ell-1} - \frac{1}{|\operatorname{\mathrm{GL}}_2(\mathbb{Z}/\ell\mathbb{Z})|}\right) \prod_{\substack{\ell \mid (n,L) \\ \ell\nmid k-1}} \left(\frac{1}{\ell-1}\right) \prod_{\substack{\ell \mid L \\ \ell \nmid n}} \left( 1 - \frac{1}{|\operatorname{\mathrm{GL}}_2(\mathbb{Z}/\ell\mathbb{Z})|}\right) \\ &= \frac{1}{\phi(n_1)} \prod_{\substack{\ell \mid (n,L) \\ \ell \mid k-1}}\left(1-\frac{\phi(\ell)}{|\operatorname{\mathrm{GL}}_2(\mathbb{Z}/\ell\mathbb{Z})|}\right) \prod_{\substack{\ell \mid L \\ \ell \nmid n}} \left( 1 - \frac{1}{|\operatorname{\mathrm{GL}}_2(\mathbb{Z}/\ell\mathbb{Z})|}\right).\nonumber \end{align} $$
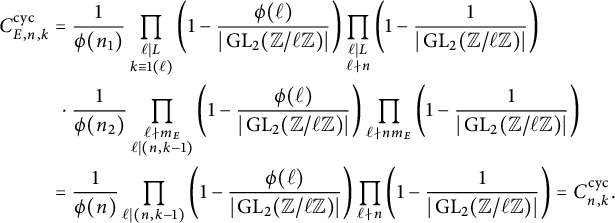 $$ \begin{align*} C^{\operatorname{\mathrm{cyc}}}_{E,n,k} = & \ \frac{1}{\phi(n_1)} \prod_{\substack{\ell \mid L \\ k \equiv 1 (\ell)}}\left(1-\frac{\phi(\ell)}{|\operatorname{\mathrm{GL}}_2(\mathbb{Z}/\ell\mathbb{Z})|}\right) \prod_{\substack{\ell \mid L \\ \ell \nmid n}} \left( 1 - \frac{1}{|\operatorname{\mathrm{GL}}_2(\mathbb{Z}/\ell\mathbb{Z})|}\right) \\ \cdot & \ \frac{1}{\phi(n_2)} \prod_{\substack{\ell \nmid m_E \\ \ell \mid (n,k-1) }}\left(1- \frac{\phi(\ell)}{|\operatorname{\mathrm{GL}}_2(\mathbb{Z}/\ell\mathbb{Z})|}\right) \prod_{\ell \nmid nm_E} \left( 1 - \frac{1}{|\operatorname{\mathrm{GL}}_2(\mathbb{Z}/\ell\mathbb{Z})|}\right) \\ = & \ \frac{1}{\phi(n)} \prod_{\substack{\ell \mid (n,k-1)}} \left( 1 - \frac{\phi(\ell)}{|\operatorname{\mathrm{GL}}_2(\mathbb{Z}/\ell\mathbb{Z})|}\right) \prod_{\ell \nmid n} \left( 1 - \frac{1}{|\operatorname{\mathrm{GL}}_2(\mathbb{Z}/\ell\mathbb{Z})|}\right) = C^{\operatorname{\mathrm{cyc}}}_{n,k}. \end{align*} $$
$$ \begin{align*} C^{\operatorname{\mathrm{cyc}}}_{E,n,k} = & \ \frac{1}{\phi(n_1)} \prod_{\substack{\ell \mid L \\ k \equiv 1 (\ell)}}\left(1-\frac{\phi(\ell)}{|\operatorname{\mathrm{GL}}_2(\mathbb{Z}/\ell\mathbb{Z})|}\right) \prod_{\substack{\ell \mid L \\ \ell \nmid n}} \left( 1 - \frac{1}{|\operatorname{\mathrm{GL}}_2(\mathbb{Z}/\ell\mathbb{Z})|}\right) \\ \cdot & \ \frac{1}{\phi(n_2)} \prod_{\substack{\ell \nmid m_E \\ \ell \mid (n,k-1) }}\left(1- \frac{\phi(\ell)}{|\operatorname{\mathrm{GL}}_2(\mathbb{Z}/\ell\mathbb{Z})|}\right) \prod_{\ell \nmid nm_E} \left( 1 - \frac{1}{|\operatorname{\mathrm{GL}}_2(\mathbb{Z}/\ell\mathbb{Z})|}\right) \\ = & \ \frac{1}{\phi(n)} \prod_{\substack{\ell \mid (n,k-1)}} \left( 1 - \frac{\phi(\ell)}{|\operatorname{\mathrm{GL}}_2(\mathbb{Z}/\ell\mathbb{Z})|}\right) \prod_{\ell \nmid n} \left( 1 - \frac{1}{|\operatorname{\mathrm{GL}}_2(\mathbb{Z}/\ell\mathbb{Z})|}\right) = C^{\operatorname{\mathrm{cyc}}}_{n,k}. \end{align*} $$
Hence, we obtain that
![]() $C^{\operatorname {\mathrm {cyc}}}_{E,n,k} = C^{\operatorname {\mathrm {cyc}}}_{n,k}$
if
$C^{\operatorname {\mathrm {cyc}}}_{E,n,k} = C^{\operatorname {\mathrm {cyc}}}_{n,k}$
if
![]() $m_E\nmid L$
.
$m_E\nmid L$
.
Similarly, for the Koblitz case, applying Lemma 5.2.(2), we see
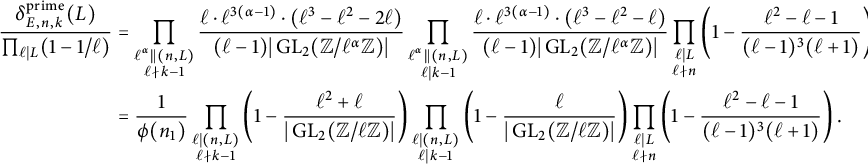 $$ \begin{align} \frac{\delta_{E,n,k}^{\operatorname{\mathrm{prime}}}(L)}{\prod_{\ell \mid L}(1-1/\ell)} &= \prod_{\substack{\ell^{\alpha} \parallel (n,L) \\ \ell\nmid k-1}} \frac{\ell \cdot \ell^{3(\alpha-1)} \cdot (\ell^3-\ell^2-2\ell)}{(\ell-1) |\operatorname{\mathrm{GL}}_2(\mathbb{Z}/\ell^{\alpha}\mathbb{Z})|} \prod_{\substack{\ell^{\alpha} \parallel (n,L) \\ \ell\mid k-1}} \frac{\ell \cdot \ell^{3(\alpha-1)}\cdot(\ell^3-\ell^2-\ell)}{(\ell-1)|\operatorname{\mathrm{GL}}_2(\mathbb{Z}/\ell^{\alpha}\mathbb{Z})|} \prod_{\substack{\ell \mid L \\ \ell \nmid n}} \left( 1 - \frac{\ell^2-\ell-1}{(\ell-1)^3(\ell+1)} \right) \\ &= \frac{1}{\phi(n_1)} \prod_{\substack{\ell \mid (n,L) \\\ell\nmid k-1}} \left(1 - \frac{\ell^2+\ell}{|\operatorname{\mathrm{GL}}_2(\mathbb{Z}/\ell\mathbb{Z})|}\right)\prod_{\substack{\ell \mid (n,L) \\\ell\mid k-1}}\left( 1 - \frac{\ell}{|\operatorname{\mathrm{GL}}_2(\mathbb{Z}/\ell\mathbb{Z})|}\right) \prod_{\substack{\ell \mid L \\ \ell \nmid n}} \left( 1 - \frac{\ell^2-\ell-1}{(\ell-1)^3(\ell+1)} \right).\nonumber \end{align} $$
$$ \begin{align} \frac{\delta_{E,n,k}^{\operatorname{\mathrm{prime}}}(L)}{\prod_{\ell \mid L}(1-1/\ell)} &= \prod_{\substack{\ell^{\alpha} \parallel (n,L) \\ \ell\nmid k-1}} \frac{\ell \cdot \ell^{3(\alpha-1)} \cdot (\ell^3-\ell^2-2\ell)}{(\ell-1) |\operatorname{\mathrm{GL}}_2(\mathbb{Z}/\ell^{\alpha}\mathbb{Z})|} \prod_{\substack{\ell^{\alpha} \parallel (n,L) \\ \ell\mid k-1}} \frac{\ell \cdot \ell^{3(\alpha-1)}\cdot(\ell^3-\ell^2-\ell)}{(\ell-1)|\operatorname{\mathrm{GL}}_2(\mathbb{Z}/\ell^{\alpha}\mathbb{Z})|} \prod_{\substack{\ell \mid L \\ \ell \nmid n}} \left( 1 - \frac{\ell^2-\ell-1}{(\ell-1)^3(\ell+1)} \right) \\ &= \frac{1}{\phi(n_1)} \prod_{\substack{\ell \mid (n,L) \\\ell\nmid k-1}} \left(1 - \frac{\ell^2+\ell}{|\operatorname{\mathrm{GL}}_2(\mathbb{Z}/\ell\mathbb{Z})|}\right)\prod_{\substack{\ell \mid (n,L) \\\ell\mid k-1}}\left( 1 - \frac{\ell}{|\operatorname{\mathrm{GL}}_2(\mathbb{Z}/\ell\mathbb{Z})|}\right) \prod_{\substack{\ell \mid L \\ \ell \nmid n}} \left( 1 - \frac{\ell^2-\ell-1}{(\ell-1)^3(\ell+1)} \right).\nonumber \end{align} $$
Thus, Proposition 4.4, Lemma 4.5, and (51) give
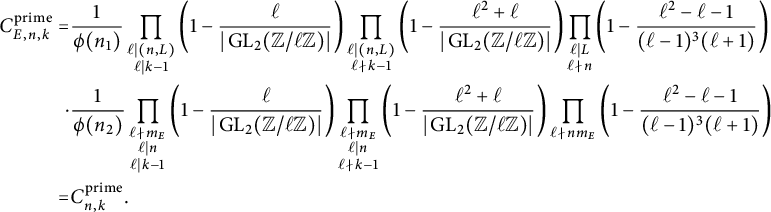 $$ \begin{align*} C^{\operatorname{\mathrm{prime}}}_{E,n,k} = &\frac{1}{\phi(n_1)} \prod_{\substack{\ell \mid (n,L) \\ \ell\mid k-1}}\left( 1 - \frac{\ell}{|\operatorname{\mathrm{GL}}_2(\mathbb{Z}/\ell\mathbb{Z})|}\right) \prod_{\substack{\ell \mid (n,L) \\ \ell\nmid k-1}} \left(1 - \frac{\ell^2+\ell}{|\operatorname{\mathrm{GL}}_2(\mathbb{Z}/\ell\mathbb{Z})|}\right) \prod_{\substack{\ell \mid L \\ \ell \nmid n}} \left( 1 - \frac{\ell^2-\ell-1}{(\ell-1)^3(\ell+1)} \right) \\ \cdot &\frac{1}{\phi(n_2)} \prod_{\substack{\ell \nmid m_E \\ \ell \mid n \\ \ell\mid k-1}} \left(1 - \frac{\ell}{|\operatorname{\mathrm{GL}}_2(\mathbb{Z}/\ell\mathbb{Z})|}\right) \prod_{\substack{\ell \nmid m_E \\ \ell \mid n \\\ell\nmid k-1}}\left(1-\frac{\ell^2+\ell}{|\operatorname{\mathrm{GL}}_2(\mathbb{Z}/\ell\mathbb{Z})|}\right) \prod_{\ell \nmid nm_E}\left(1-\frac{\ell^2-\ell-1}{(\ell-1)^3(\ell+1)}\right) \\ =& C^{\operatorname{\mathrm{prime}}}_{n,k}. \end{align*} $$
$$ \begin{align*} C^{\operatorname{\mathrm{prime}}}_{E,n,k} = &\frac{1}{\phi(n_1)} \prod_{\substack{\ell \mid (n,L) \\ \ell\mid k-1}}\left( 1 - \frac{\ell}{|\operatorname{\mathrm{GL}}_2(\mathbb{Z}/\ell\mathbb{Z})|}\right) \prod_{\substack{\ell \mid (n,L) \\ \ell\nmid k-1}} \left(1 - \frac{\ell^2+\ell}{|\operatorname{\mathrm{GL}}_2(\mathbb{Z}/\ell\mathbb{Z})|}\right) \prod_{\substack{\ell \mid L \\ \ell \nmid n}} \left( 1 - \frac{\ell^2-\ell-1}{(\ell-1)^3(\ell+1)} \right) \\ \cdot &\frac{1}{\phi(n_2)} \prod_{\substack{\ell \nmid m_E \\ \ell \mid n \\ \ell\mid k-1}} \left(1 - \frac{\ell}{|\operatorname{\mathrm{GL}}_2(\mathbb{Z}/\ell\mathbb{Z})|}\right) \prod_{\substack{\ell \nmid m_E \\ \ell \mid n \\\ell\nmid k-1}}\left(1-\frac{\ell^2+\ell}{|\operatorname{\mathrm{GL}}_2(\mathbb{Z}/\ell\mathbb{Z})|}\right) \prod_{\ell \nmid nm_E}\left(1-\frac{\ell^2-\ell-1}{(\ell-1)^3(\ell+1)}\right) \\ =& C^{\operatorname{\mathrm{prime}}}_{n,k}. \end{align*} $$
This completes the proof of the theorem for the case where
![]() $m_E \nmid L$
.
$m_E \nmid L$
.
Now, suppose that
![]() $m_E\mid L$
. This case is a bit more involved. First, we recall from Section 2.2 the definition of
$m_E\mid L$
. This case is a bit more involved. First, we recall from Section 2.2 the definition of
![]() $\psi _{\ell ^{\alpha }}$
and the fact that
$\psi _{\ell ^{\alpha }}$
and the fact that
![]() $G_E(L) = \ker \psi _L$
. By [Reference Jones31, Lemma 16] and (49) we have
$G_E(L) = \ker \psi _L$
. By [Reference Jones31, Lemma 16] and (49) we have
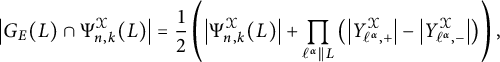 $$ \begin{align} \left|G_E(L)\cap \Psi^{\mathcal{X}}_{n,k}(L)\right|= \frac{1}{2}\left(\left|\Psi^{\mathcal{X}}_{n,k}(L)\right| +\prod_{\ell^{\alpha}\parallel L}\left(\left|Y^{\mathcal{X}}_{\ell^{\alpha}, +}\right|-\left|Y^{\mathcal{X}}_{\ell^{\alpha}, -}\right|\right)\right), \end{align} $$
$$ \begin{align} \left|G_E(L)\cap \Psi^{\mathcal{X}}_{n,k}(L)\right|= \frac{1}{2}\left(\left|\Psi^{\mathcal{X}}_{n,k}(L)\right| +\prod_{\ell^{\alpha}\parallel L}\left(\left|Y^{\mathcal{X}}_{\ell^{\alpha}, +}\right|-\left|Y^{\mathcal{X}}_{\ell^{\alpha}, -}\right|\right)\right), \end{align} $$
for
![]() $\mathcal {X}\in \{\operatorname {\mathrm {cyc}}, \operatorname {\mathrm {prime}}\}$
, where
$\mathcal {X}\in \{\operatorname {\mathrm {cyc}}, \operatorname {\mathrm {prime}}\}$
, where
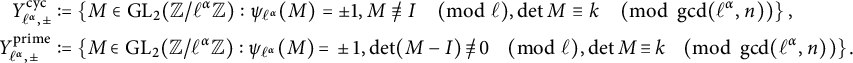
The sets
![]() $Y^{\operatorname {\mathrm {cyc}}}_{\ell ^{\alpha }, +}$
,
$Y^{\operatorname {\mathrm {cyc}}}_{\ell ^{\alpha }, +}$
,
![]() $Y^{\operatorname {\mathrm {cyc}}}_{\ell ^{\alpha }, -}$
,
$Y^{\operatorname {\mathrm {cyc}}}_{\ell ^{\alpha }, -}$
,
![]() $Y^{\operatorname {\mathrm {prime}}}_{\ell ^{\alpha }, +}$
, and
$Y^{\operatorname {\mathrm {prime}}}_{\ell ^{\alpha }, +}$
, and
![]() $Y^{\operatorname {\mathrm {prime}}}_{\ell ^{\alpha }, -}$
all depend on n and k, though we do not include this dependence in the notation for brevity. We first focus on the size of
$Y^{\operatorname {\mathrm {prime}}}_{\ell ^{\alpha }, -}$
all depend on n and k, though we do not include this dependence in the notation for brevity. We first focus on the size of
![]() $|Y^{\mathcal {X}}_{\ell ^\alpha ,+}| - |Y^{\mathcal {X}}_{\ell ^\alpha ,-}|$
for primes
$|Y^{\mathcal {X}}_{\ell ^\alpha ,+}| - |Y^{\mathcal {X}}_{\ell ^\alpha ,-}|$
for primes
![]() $\ell $
dividing
$\ell $
dividing
![]() $L^{\operatorname {\mathrm {odd}}}$
.
$L^{\operatorname {\mathrm {odd}}}$
.
Lemma 5.3 We have
-
(1)
 $$ \begin{align*} \displaystyle\prod_{\substack{\ell^{\alpha}\parallel L^{\operatorname{\mathrm{odd}}}}}\left(|Y^{\operatorname{\mathrm{cyc}}}_{\ell^{\alpha}, +}|-|Y^{\operatorname{\mathrm{cyc}}}_{\ell^{\alpha}, -}| \right) & = \\ & \hspace{-.5cm} \prod_{\substack{\ell \mid L^{\operatorname{\mathrm{odd}}}\\ \ell \nmid n}} (-1)\prod_{\substack{\ell^{\alpha}\parallel (n, L^{\operatorname{\mathrm{odd}}})\\ \ell\mid k-1}} \ell^{3(\alpha-1)}(\ell^3-\ell-1) \prod_{\substack{\ell^{\alpha}\parallel (n, L^{\operatorname{\mathrm{odd}}})\\ \ell\nmid k-1}}\left(\frac{k}{\ell}\right)\ell^{3(\alpha-1)}(\ell^3-\ell). \end{align*} $$
$$ \begin{align*} \displaystyle\prod_{\substack{\ell^{\alpha}\parallel L^{\operatorname{\mathrm{odd}}}}}\left(|Y^{\operatorname{\mathrm{cyc}}}_{\ell^{\alpha}, +}|-|Y^{\operatorname{\mathrm{cyc}}}_{\ell^{\alpha}, -}| \right) & = \\ & \hspace{-.5cm} \prod_{\substack{\ell \mid L^{\operatorname{\mathrm{odd}}}\\ \ell \nmid n}} (-1)\prod_{\substack{\ell^{\alpha}\parallel (n, L^{\operatorname{\mathrm{odd}}})\\ \ell\mid k-1}} \ell^{3(\alpha-1)}(\ell^3-\ell-1) \prod_{\substack{\ell^{\alpha}\parallel (n, L^{\operatorname{\mathrm{odd}}})\\ \ell\nmid k-1}}\left(\frac{k}{\ell}\right)\ell^{3(\alpha-1)}(\ell^3-\ell). \end{align*} $$
-
(2)
 $$ \begin{align*} \displaystyle\prod_{\substack{\ell^{\alpha}\parallel L^{\operatorname{\mathrm{odd}}}}}\left(|Y^{\operatorname{\mathrm{prime}}}_{\ell^{\alpha}, +}|-|Y^{\operatorname{\mathrm{prime}}}_{\ell^{\alpha}, -}| \right) & = \\ & \hspace{-1cm}\prod_{\substack{\ell \mid L^{\operatorname{\mathrm{odd}}}\\ \ell \nmid n}} \ell \prod_{\substack{\ell^{\alpha}\parallel (n, L^{\operatorname{\mathrm{odd}}})\\ \ell\mid k-1}} \ell^{3(\alpha-1)}(\ell^3-\ell^2-\ell) \prod_{\substack{\ell^{\alpha}\parallel (n, L^{\operatorname{\mathrm{odd}}})\\ \ell\nmid k-1}}\left(\frac{k}{\ell}\right)\ell^{3(\alpha-1)}(\ell^3-\ell^2-2\ell). \end{align*} $$
$$ \begin{align*} \displaystyle\prod_{\substack{\ell^{\alpha}\parallel L^{\operatorname{\mathrm{odd}}}}}\left(|Y^{\operatorname{\mathrm{prime}}}_{\ell^{\alpha}, +}|-|Y^{\operatorname{\mathrm{prime}}}_{\ell^{\alpha}, -}| \right) & = \\ & \hspace{-1cm}\prod_{\substack{\ell \mid L^{\operatorname{\mathrm{odd}}}\\ \ell \nmid n}} \ell \prod_{\substack{\ell^{\alpha}\parallel (n, L^{\operatorname{\mathrm{odd}}})\\ \ell\mid k-1}} \ell^{3(\alpha-1)}(\ell^3-\ell^2-\ell) \prod_{\substack{\ell^{\alpha}\parallel (n, L^{\operatorname{\mathrm{odd}}})\\ \ell\nmid k-1}}\left(\frac{k}{\ell}\right)\ell^{3(\alpha-1)}(\ell^3-\ell^2-2\ell). \end{align*} $$
Proof From the definition of
![]() $\psi _{\ell ^{\alpha }}$
for an odd prime
$\psi _{\ell ^{\alpha }}$
for an odd prime
![]() $\ell \mid L$
, we have
$\ell \mid L$
, we have
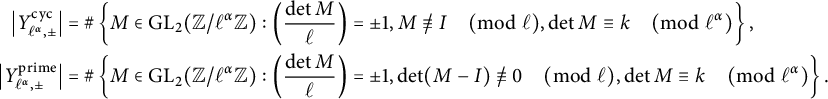 $$ \begin{align*} \left|Y^{\operatorname{\mathrm{cyc}}}_{\ell^{\alpha}, \pm}\right| &=\#\left\{M \in \operatorname{\mathrm{GL}}_2(\mathbb{Z}/\ell^{\alpha} \mathbb{Z}) : \left(\frac{\operatorname{det} M}{\ell}\right) = \pm 1, M \not \equiv I \quad\pmod \ell, \operatorname{det} M \equiv k \quad\pmod {\ell^{\alpha}} \right\}, \\ \left|Y^{\operatorname{\mathrm{prime}}}_{{\ell^\alpha},\pm}\right| &= \#\left\{M \in \operatorname{\mathrm{GL}}_2(\mathbb{Z}/\ell^\alpha\mathbb{Z}) : \left( \frac{\operatorname{det} M}{\ell}\right) = \pm 1, \operatorname{det}(M-I) \not \equiv 0 \quad\pmod \ell, \operatorname{det} M \equiv k \quad\pmod {\ell^\alpha} \right\}. \end{align*} $$
$$ \begin{align*} \left|Y^{\operatorname{\mathrm{cyc}}}_{\ell^{\alpha}, \pm}\right| &=\#\left\{M \in \operatorname{\mathrm{GL}}_2(\mathbb{Z}/\ell^{\alpha} \mathbb{Z}) : \left(\frac{\operatorname{det} M}{\ell}\right) = \pm 1, M \not \equiv I \quad\pmod \ell, \operatorname{det} M \equiv k \quad\pmod {\ell^{\alpha}} \right\}, \\ \left|Y^{\operatorname{\mathrm{prime}}}_{{\ell^\alpha},\pm}\right| &= \#\left\{M \in \operatorname{\mathrm{GL}}_2(\mathbb{Z}/\ell^\alpha\mathbb{Z}) : \left( \frac{\operatorname{det} M}{\ell}\right) = \pm 1, \operatorname{det}(M-I) \not \equiv 0 \quad\pmod \ell, \operatorname{det} M \equiv k \quad\pmod {\ell^\alpha} \right\}. \end{align*} $$
By Corollaries 3.2 and 3.4, it is easy to check that
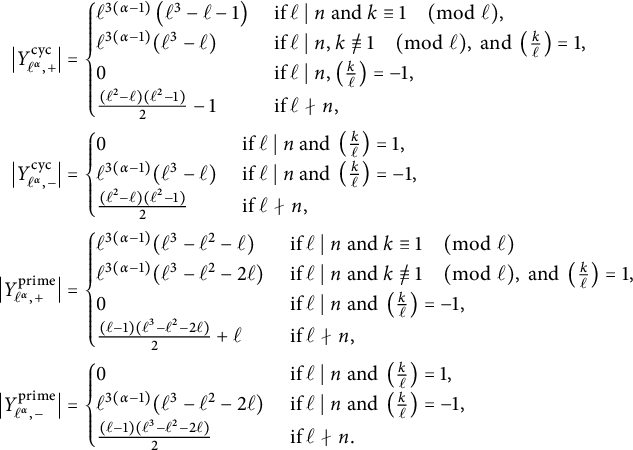 $$ \begin{align*} \left|Y^{\operatorname{\mathrm{cyc}}}_{\ell^{\alpha},+}\right| &= \begin{cases} \ell^{3(\alpha-1)} \left(\ell^3-\ell-1 \right) & \text{ if } \ell\mid n \text{ and } k \equiv 1 \quad\pmod {\ell}, \\ \ell^{3(\alpha-1)}(\ell^3-\ell) & \text{ if } \ell\mid n, k \not \equiv 1 \quad\pmod {\ell}, \text{ and } \left(\frac{k}{\ell}\right) = 1, \\ 0 & \text{ if } \ell\mid n, \left(\frac{k}{\ell}\right) = -1, \\ \frac{(\ell^2-\ell)(\ell^2-1)}{2}-1 & \text{ if } \ell \nmid n, \end{cases} \\ \left| Y^{\operatorname{\mathrm{cyc}}}_{\ell^{\alpha},-}\right| &= \begin{cases} 0 & \text{ if } \ell\mid n \text{ and } \left(\frac{k}{\ell}\right) = 1, \\ \ell^{3(\alpha-1)}(\ell^3-\ell) & \text{ if } \ell\mid n \text{ and } \left(\frac{k}{\ell}\right) = -1,\\ \frac{(\ell^2-\ell)(\ell^2-1)}{2} & \text{ if } \ell \nmid n, \end{cases} \\ \left|Y^{\operatorname{\mathrm{prime}}}_{\ell^{\alpha},+}\right| & = \begin{cases} \ell^{3(\alpha-1)} (\ell^3-\ell^2-\ell) & \text{ if } \ell\mid n\text{ and } k \equiv 1 \quad\pmod \ell \\ \ell^{3(\alpha-1)} (\ell^3-\ell^2-2\ell) & \text{ if } \ell\mid n \text{ and } k \not \equiv 1 \quad\pmod \ell, \text{ and } \left(\frac{k}{\ell}\right) = 1, \\ 0 & \text{ if } \ell\mid n \text{ and } \left(\frac{k}{\ell}\right) = - 1, \\ \frac{(\ell-1)(\ell^3-\ell^2-2\ell)}{2} + \ell & \text{ if } \ell \nmid n, \end{cases} \\ \left|Y^{\operatorname{\mathrm{prime}}}_{\ell^{\alpha}, -}\right| &= \begin{cases} 0 & \text{ if }\ell \mid n \text{ and } \left(\frac{k}{\ell}\right) = 1, \\ \ell^{3(\alpha-1)} (\ell^3-\ell^2-2\ell) & \text{ if } \ell\mid n \text{ and } \left(\frac{k}{\ell}\right) = - 1, \\ \frac{(\ell-1)(\ell^3-\ell^2-2\ell)}{2} & \text{ if } \ell \nmid n. \end{cases} \end{align*} $$
$$ \begin{align*} \left|Y^{\operatorname{\mathrm{cyc}}}_{\ell^{\alpha},+}\right| &= \begin{cases} \ell^{3(\alpha-1)} \left(\ell^3-\ell-1 \right) & \text{ if } \ell\mid n \text{ and } k \equiv 1 \quad\pmod {\ell}, \\ \ell^{3(\alpha-1)}(\ell^3-\ell) & \text{ if } \ell\mid n, k \not \equiv 1 \quad\pmod {\ell}, \text{ and } \left(\frac{k}{\ell}\right) = 1, \\ 0 & \text{ if } \ell\mid n, \left(\frac{k}{\ell}\right) = -1, \\ \frac{(\ell^2-\ell)(\ell^2-1)}{2}-1 & \text{ if } \ell \nmid n, \end{cases} \\ \left| Y^{\operatorname{\mathrm{cyc}}}_{\ell^{\alpha},-}\right| &= \begin{cases} 0 & \text{ if } \ell\mid n \text{ and } \left(\frac{k}{\ell}\right) = 1, \\ \ell^{3(\alpha-1)}(\ell^3-\ell) & \text{ if } \ell\mid n \text{ and } \left(\frac{k}{\ell}\right) = -1,\\ \frac{(\ell^2-\ell)(\ell^2-1)}{2} & \text{ if } \ell \nmid n, \end{cases} \\ \left|Y^{\operatorname{\mathrm{prime}}}_{\ell^{\alpha},+}\right| & = \begin{cases} \ell^{3(\alpha-1)} (\ell^3-\ell^2-\ell) & \text{ if } \ell\mid n\text{ and } k \equiv 1 \quad\pmod \ell \\ \ell^{3(\alpha-1)} (\ell^3-\ell^2-2\ell) & \text{ if } \ell\mid n \text{ and } k \not \equiv 1 \quad\pmod \ell, \text{ and } \left(\frac{k}{\ell}\right) = 1, \\ 0 & \text{ if } \ell\mid n \text{ and } \left(\frac{k}{\ell}\right) = - 1, \\ \frac{(\ell-1)(\ell^3-\ell^2-2\ell)}{2} + \ell & \text{ if } \ell \nmid n, \end{cases} \\ \left|Y^{\operatorname{\mathrm{prime}}}_{\ell^{\alpha}, -}\right| &= \begin{cases} 0 & \text{ if }\ell \mid n \text{ and } \left(\frac{k}{\ell}\right) = 1, \\ \ell^{3(\alpha-1)} (\ell^3-\ell^2-2\ell) & \text{ if } \ell\mid n \text{ and } \left(\frac{k}{\ell}\right) = - 1, \\ \frac{(\ell-1)(\ell^3-\ell^2-2\ell)}{2} & \text{ if } \ell \nmid n. \end{cases} \end{align*} $$
The result now follows from some simple computations.
Finally, we evaluate
![]() $|Y^{\mathcal {X}}_{\ell ^{\alpha }, +}|-|Y^{\mathcal {X}}_{\ell ^{\alpha }, -}|$
when
$|Y^{\mathcal {X}}_{\ell ^{\alpha }, +}|-|Y^{\mathcal {X}}_{\ell ^{\alpha }, -}|$
when
![]() $\ell =2$
.
$\ell =2$
.
Lemma 5.4 For fixed
![]() $\Delta ^{\prime }$
and k, let
$\Delta ^{\prime }$
and k, let
![]() $\tau $
be defined as in Definition 5.1. Then
$\tau $
be defined as in Definition 5.1. Then
-
(1)
 $|Y^{\operatorname {\mathrm {cyc}}}_{2^\alpha ,+}| - |Y^{\operatorname {\mathrm {cyc}}}_{2^{\alpha },-}| = \tau \cdot 2^{3(\alpha -1)}$
$|Y^{\operatorname {\mathrm {cyc}}}_{2^\alpha ,+}| - |Y^{\operatorname {\mathrm {cyc}}}_{2^{\alpha },-}| = \tau \cdot 2^{3(\alpha -1)}$
-
(2)
 $|Y^{\operatorname {\mathrm {prime}}}_{2^{\alpha },+}| - |Y^{\operatorname {\mathrm {prime}}}_{2^{\alpha },-}| = -(2\tau ) \cdot 2^{3(\alpha -1)}.$
$|Y^{\operatorname {\mathrm {prime}}}_{2^{\alpha },+}| - |Y^{\operatorname {\mathrm {prime}}}_{2^{\alpha },-}| = -(2\tau ) \cdot 2^{3(\alpha -1)}.$
Proof First, we assume
![]() $\Delta ^{\prime }\equiv 1\ \pmod 4$
. Then, by the definition of
$\Delta ^{\prime }\equiv 1\ \pmod 4$
. Then, by the definition of
![]() $\psi _{2^{\alpha }}(\cdot )$
,
$\psi _{2^{\alpha }}(\cdot )$
,
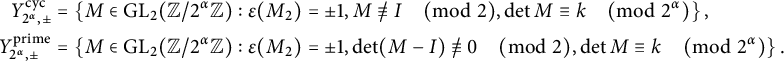 $$ \begin{align*} Y^{\operatorname{\mathrm{cyc}}}_{2^{\alpha},\pm} &= \left\{M \in \operatorname{\mathrm{GL}}_2(\mathbb{Z}/2^\alpha\mathbb{Z}) : \epsilon(M_2) = \pm 1, M \not \equiv I \quad\pmod 2, \operatorname{det} M \equiv k \quad\pmod {2^{\alpha}}\right\}, \\ Y^{\operatorname{\mathrm{prime}}}_{2^{\alpha},\pm} &= \left\{M \in \operatorname{\mathrm{GL}}_2(\mathbb{Z}/2^\alpha\mathbb{Z}) : \epsilon(M_2) = \pm 1, \operatorname{det}(M-I) \not \equiv 0 \quad\pmod 2, \operatorname{det} M \equiv k \quad\pmod {2^{\alpha}}\right\}. \end{align*} $$
$$ \begin{align*} Y^{\operatorname{\mathrm{cyc}}}_{2^{\alpha},\pm} &= \left\{M \in \operatorname{\mathrm{GL}}_2(\mathbb{Z}/2^\alpha\mathbb{Z}) : \epsilon(M_2) = \pm 1, M \not \equiv I \quad\pmod 2, \operatorname{det} M \equiv k \quad\pmod {2^{\alpha}}\right\}, \\ Y^{\operatorname{\mathrm{prime}}}_{2^{\alpha},\pm} &= \left\{M \in \operatorname{\mathrm{GL}}_2(\mathbb{Z}/2^\alpha\mathbb{Z}) : \epsilon(M_2) = \pm 1, \operatorname{det}(M-I) \not \equiv 0 \quad\pmod 2, \operatorname{det} M \equiv k \quad\pmod {2^{\alpha}}\right\}. \end{align*} $$
Let
![]() $h^{\operatorname {\mathrm {cyc}}}_{\pm } = |Y^{\operatorname {\mathrm {cyc}}}_{2,\pm }|$
. In the case where
$h^{\operatorname {\mathrm {cyc}}}_{\pm } = |Y^{\operatorname {\mathrm {cyc}}}_{2,\pm }|$
. In the case where
![]() $\alpha = 1$
, it is clear that
$\alpha = 1$
, it is clear that
![]() $h^{\operatorname {\mathrm {cyc}}}_+=2$
and
$h^{\operatorname {\mathrm {cyc}}}_+=2$
and
![]() $h^{\operatorname {\mathrm {cyc}}}_- =3$
. For
$h^{\operatorname {\mathrm {cyc}}}_- =3$
. For
![]() $\alpha \geq 2$
, by Lemma 3.1, we obtain
$\alpha \geq 2$
, by Lemma 3.1, we obtain
and hence
![]() $|Y^{\operatorname {\mathrm {cyc}}}_{2^\alpha ,+}| - |Y^{\operatorname {\mathrm {cyc}}}_{2^\alpha ,-}| = -2^{3(\alpha -1)}$
.
$|Y^{\operatorname {\mathrm {cyc}}}_{2^\alpha ,+}| - |Y^{\operatorname {\mathrm {cyc}}}_{2^\alpha ,-}| = -2^{3(\alpha -1)}$
.
Let us check the size of
![]() $Y^{\operatorname {\mathrm {prime}}}_{2^{\alpha },\pm }$
. In the case where
$Y^{\operatorname {\mathrm {prime}}}_{2^{\alpha },\pm }$
. In the case where
![]() $\alpha = 1$
, we have that
$\alpha = 1$
, we have that
 $$\begin{align*}Y^{\operatorname{\mathrm{prime}}}_{2,+} = \left\{ \begin{pmatrix} 1 & 1 \\ 1 & 0 \end{pmatrix}, \begin{pmatrix} 0 & 1 \\ 1 & 1 \end{pmatrix} \right\} \quad \text{and} \quad Y^{\operatorname{\mathrm{prime}}}_{2,-} = \emptyset. \end{align*}$$
$$\begin{align*}Y^{\operatorname{\mathrm{prime}}}_{2,+} = \left\{ \begin{pmatrix} 1 & 1 \\ 1 & 0 \end{pmatrix}, \begin{pmatrix} 0 & 1 \\ 1 & 1 \end{pmatrix} \right\} \quad \text{and} \quad Y^{\operatorname{\mathrm{prime}}}_{2,-} = \emptyset. \end{align*}$$
Setting ![]() , we see that
, we see that
![]() $h^{\operatorname {\mathrm {prime}}}_+ = 2$
and
$h^{\operatorname {\mathrm {prime}}}_+ = 2$
and
![]() $h^{\operatorname {\mathrm {prime}}}_- =0$
. By Lemma 3.1, we obtain
$h^{\operatorname {\mathrm {prime}}}_- =0$
. By Lemma 3.1, we obtain
and hence
![]() $|Y^{\operatorname {\mathrm {prime}}}_{2^{\alpha },+}| -|Y^{\operatorname {\mathrm {prime}}}_{2^{\alpha },-}| = 2 \cdot 2^{3(\alpha -1)}.$
$|Y^{\operatorname {\mathrm {prime}}}_{2^{\alpha },+}| -|Y^{\operatorname {\mathrm {prime}}}_{2^{\alpha },-}| = 2 \cdot 2^{3(\alpha -1)}.$
Next, we assume
![]() $\Delta ^{\prime }\equiv 3\ \pmod 4$
. Then, by the definition of
$\Delta ^{\prime }\equiv 3\ \pmod 4$
. Then, by the definition of
![]() $\psi _{2^{\alpha }}(\cdot )$
, we have
$\psi _{2^{\alpha }}(\cdot )$
, we have
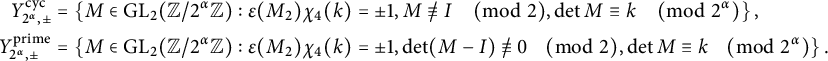 $$ \begin{align*} Y^{\operatorname{\mathrm{cyc}}}_{2^{\alpha},\pm} &= \left\{M \in \operatorname{\mathrm{GL}}_2(\mathbb{Z}/2^\alpha\mathbb{Z}) : \epsilon(M_2)\chi_4(k) = \pm 1, M \not \equiv I \quad\pmod 2, \operatorname{det} M \equiv k \quad\pmod {2^{\alpha}}\right\}, \\ Y^{\operatorname{\mathrm{prime}}}_{2^{\alpha},\pm} &= \left\{M \in \operatorname{\mathrm{GL}}_2(\mathbb{Z}/2^\alpha\mathbb{Z}) : \epsilon(M_2)\chi_4(k) = \pm 1, \operatorname{det}(M-I) \not \equiv 0 \quad\!\pmod 2, \operatorname{det} M \equiv k \!\quad\pmod {2^{\alpha}}\right\}. \end{align*} $$
$$ \begin{align*} Y^{\operatorname{\mathrm{cyc}}}_{2^{\alpha},\pm} &= \left\{M \in \operatorname{\mathrm{GL}}_2(\mathbb{Z}/2^\alpha\mathbb{Z}) : \epsilon(M_2)\chi_4(k) = \pm 1, M \not \equiv I \quad\pmod 2, \operatorname{det} M \equiv k \quad\pmod {2^{\alpha}}\right\}, \\ Y^{\operatorname{\mathrm{prime}}}_{2^{\alpha},\pm} &= \left\{M \in \operatorname{\mathrm{GL}}_2(\mathbb{Z}/2^\alpha\mathbb{Z}) : \epsilon(M_2)\chi_4(k) = \pm 1, \operatorname{det}(M-I) \not \equiv 0 \quad\!\pmod 2, \operatorname{det} M \equiv k \!\quad\pmod {2^{\alpha}}\right\}. \end{align*} $$
Then
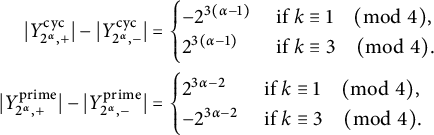 $$ \begin{align*} |Y^{\operatorname{\mathrm{cyc}}}_{2^{\alpha},+}|-|Y^{\operatorname{\mathrm{cyc}}}_{2^{\alpha},-}|&= \begin{cases} -2^{3(\alpha-1)} & \text{ if } k \equiv 1 \quad\pmod 4, \\ 2^{3(\alpha-1)} & \text{ if } k \equiv 3 \quad\pmod 4. \end{cases} \\ |Y^{\operatorname{\mathrm{prime}}}_{2^{\alpha},+}|- |Y^{\operatorname{\mathrm{prime}}}_{2^{\alpha},-}|&= \begin{cases} 2^{3\alpha-2} & \text{ if } k \equiv 1 \quad\pmod 4, \\ -2^{3\alpha-2} & \text{ if } k \equiv 3 \quad\pmod 4. \end{cases} \end{align*} $$
$$ \begin{align*} |Y^{\operatorname{\mathrm{cyc}}}_{2^{\alpha},+}|-|Y^{\operatorname{\mathrm{cyc}}}_{2^{\alpha},-}|&= \begin{cases} -2^{3(\alpha-1)} & \text{ if } k \equiv 1 \quad\pmod 4, \\ 2^{3(\alpha-1)} & \text{ if } k \equiv 3 \quad\pmod 4. \end{cases} \\ |Y^{\operatorname{\mathrm{prime}}}_{2^{\alpha},+}|- |Y^{\operatorname{\mathrm{prime}}}_{2^{\alpha},-}|&= \begin{cases} 2^{3\alpha-2} & \text{ if } k \equiv 1 \quad\pmod 4, \\ -2^{3\alpha-2} & \text{ if } k \equiv 3 \quad\pmod 4. \end{cases} \end{align*} $$
Similar arguments can be applied to deduce the results for
![]() $\Delta ^{\prime }\equiv 2\ \pmod 8$
and
$\Delta ^{\prime }\equiv 2\ \pmod 8$
and
![]() $\Delta ^{\prime }\equiv 6 \ \pmod 8$
.
$\Delta ^{\prime }\equiv 6 \ \pmod 8$
.
With the results of the above lemmas in hand, we now determine
![]() $|G_E(L) \cap \Psi ^{\mathcal {X}}_{n,k}|$
. Let us treat the cyclicity case first. By Lemma 5.4 and (52), we find that
$|G_E(L) \cap \Psi ^{\mathcal {X}}_{n,k}|$
. Let us treat the cyclicity case first. By Lemma 5.4 and (52), we find that
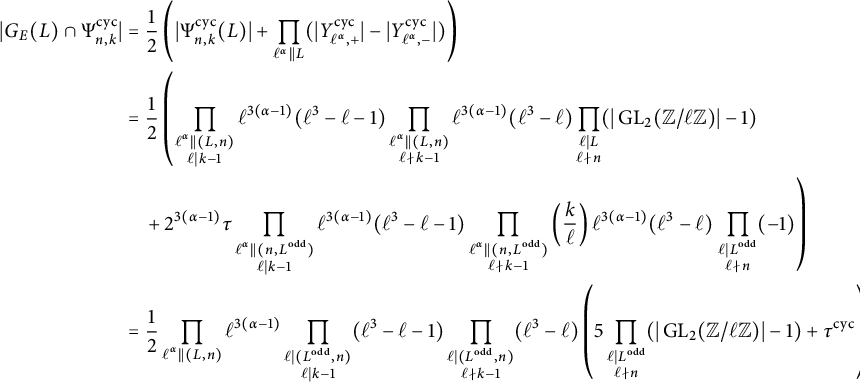 $$ \begin{align*} |G_E(L) \cap \Psi^{\operatorname{\mathrm{cyc}}}_{n,k}| &= \frac{1}{2}\left(|\Psi^{\operatorname{\mathrm{cyc}}}_{n,k}(L)| + \prod_{\ell^\alpha \parallel L}(|Y^{\operatorname{\mathrm{cyc}}}_{\ell^\alpha,+}| - |Y^{\operatorname{\mathrm{cyc}}}_{\ell^\alpha,-}| ) \right) \\ &= \frac{1}{2} \left( \prod_{\substack{\ell^\alpha \parallel (L,n) \\\ell\mid k-1}} \ell^{3(\alpha-1)}(\ell^3-\ell-1) \prod_{\substack{\ell^\alpha \parallel (L,n) \\ \ell\nmid k-1 }}\ell^{3(\alpha-1)} (\ell^3-\ell) \prod_{\substack{\ell \mid L \\ \ell \nmid n}}(|\operatorname{\mathrm{GL}}_2(\mathbb{Z}/\ell\mathbb{Z})|-1) \right. \\ &\quad + 2^{3(\alpha-1)} \tau \prod_{\substack{\ell^{\alpha}\parallel (n, L^{\operatorname{\mathrm{odd}}})\\ \ell\mid k-1}} \ell^{3(\alpha-1)}(\ell^3-\ell-1) \prod_{\substack{\ell^{\alpha}\parallel (n, L^{\operatorname{\mathrm{odd}}}) \\ \ell\nmid k-1}}\left(\frac{k}{\ell}\right)\ell^{3(\alpha-1)}(\ell^3-\ell)\left. \prod_{\substack{\ell \mid L^{\operatorname{\mathrm{odd}}}\\ \ell \nmid n}} (-1) \right) \\ & = \frac{1}{2}\prod_{\substack{\ell^\alpha \parallel (L,n)}} \ell^{3(\alpha-1)} \prod_{\substack{\ell \mid (L^{\operatorname{\mathrm{odd}}},n) \\ \ell \mid k-1}}(\ell^3-\ell-1) \prod_{\substack{\ell \mid (L^{\operatorname{\mathrm{odd}}},n) \\ \ell \nmid k-1}}(\ell^3-\ell) \left( 5\prod_{\substack{\ell \mid L^{\operatorname{\mathrm{odd}}} \\ \ell \nmid n}} (|\operatorname{\mathrm{GL}}_2(\mathbb{Z}/\ell\mathbb{Z})|-1) + \tau^{\operatorname{\mathrm{cyc}}} \right). \end{align*} $$
$$ \begin{align*} |G_E(L) \cap \Psi^{\operatorname{\mathrm{cyc}}}_{n,k}| &= \frac{1}{2}\left(|\Psi^{\operatorname{\mathrm{cyc}}}_{n,k}(L)| + \prod_{\ell^\alpha \parallel L}(|Y^{\operatorname{\mathrm{cyc}}}_{\ell^\alpha,+}| - |Y^{\operatorname{\mathrm{cyc}}}_{\ell^\alpha,-}| ) \right) \\ &= \frac{1}{2} \left( \prod_{\substack{\ell^\alpha \parallel (L,n) \\\ell\mid k-1}} \ell^{3(\alpha-1)}(\ell^3-\ell-1) \prod_{\substack{\ell^\alpha \parallel (L,n) \\ \ell\nmid k-1 }}\ell^{3(\alpha-1)} (\ell^3-\ell) \prod_{\substack{\ell \mid L \\ \ell \nmid n}}(|\operatorname{\mathrm{GL}}_2(\mathbb{Z}/\ell\mathbb{Z})|-1) \right. \\ &\quad + 2^{3(\alpha-1)} \tau \prod_{\substack{\ell^{\alpha}\parallel (n, L^{\operatorname{\mathrm{odd}}})\\ \ell\mid k-1}} \ell^{3(\alpha-1)}(\ell^3-\ell-1) \prod_{\substack{\ell^{\alpha}\parallel (n, L^{\operatorname{\mathrm{odd}}}) \\ \ell\nmid k-1}}\left(\frac{k}{\ell}\right)\ell^{3(\alpha-1)}(\ell^3-\ell)\left. \prod_{\substack{\ell \mid L^{\operatorname{\mathrm{odd}}}\\ \ell \nmid n}} (-1) \right) \\ & = \frac{1}{2}\prod_{\substack{\ell^\alpha \parallel (L,n)}} \ell^{3(\alpha-1)} \prod_{\substack{\ell \mid (L^{\operatorname{\mathrm{odd}}},n) \\ \ell \mid k-1}}(\ell^3-\ell-1) \prod_{\substack{\ell \mid (L^{\operatorname{\mathrm{odd}}},n) \\ \ell \nmid k-1}}(\ell^3-\ell) \left( 5\prod_{\substack{\ell \mid L^{\operatorname{\mathrm{odd}}} \\ \ell \nmid n}} (|\operatorname{\mathrm{GL}}_2(\mathbb{Z}/\ell\mathbb{Z})|-1) + \tau^{\operatorname{\mathrm{cyc}}} \right). \end{align*} $$
Since we are assuming that
![]() $m_E \mid L$
,
$m_E \mid L$
,
![]() $G_E(L)$
must be an index
$G_E(L)$
must be an index
![]() $2$
subgroup of
$2$
subgroup of
![]() $\operatorname {\mathrm {GL}}_2(\mathbb {Z}/L\mathbb {Z})$
. Thus, we have
$\operatorname {\mathrm {GL}}_2(\mathbb {Z}/L\mathbb {Z})$
. Thus, we have
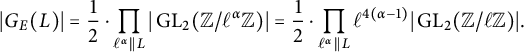 $$ \begin{align} |G_E(L)| = \frac{1}{2} \cdot \prod_{\ell^{\alpha}\parallel L}|\operatorname{\mathrm{GL}}_2(\mathbb{Z}/\ell^{\alpha}\mathbb{Z})|=\frac{1}{2} \cdot \prod_{\ell^\alpha \parallel L}\ell^{4(\alpha-1)}|\operatorname{\mathrm{GL}}_2(\mathbb{Z}/\ell\mathbb{Z})|. \end{align} $$
$$ \begin{align} |G_E(L)| = \frac{1}{2} \cdot \prod_{\ell^{\alpha}\parallel L}|\operatorname{\mathrm{GL}}_2(\mathbb{Z}/\ell^{\alpha}\mathbb{Z})|=\frac{1}{2} \cdot \prod_{\ell^\alpha \parallel L}\ell^{4(\alpha-1)}|\operatorname{\mathrm{GL}}_2(\mathbb{Z}/\ell\mathbb{Z})|. \end{align} $$
Along with Proposition 4.10 and Lemma 4.11, a short computation reveals that
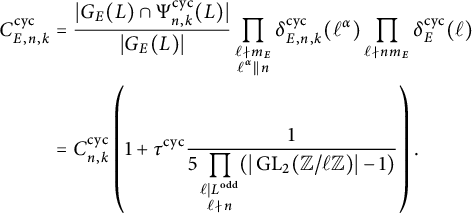 $$ \begin{align*} C_{E, n, k}^{\operatorname{\mathrm{cyc}}} & = \frac{|G_E(L) \cap \Psi^{\operatorname{\mathrm{cyc}}}_{n,k}(L)|}{|G_E(L)|} \prod_{\substack{\ell \nmid m_E \\ \ell^\alpha \parallel n}} \delta^{\operatorname{\mathrm{cyc}}}_{E,n,k}(\ell^\alpha) \prod_{\ell \nmid nm_E} \delta^{\operatorname{\mathrm{cyc}}}_{E}(\ell) \\ & =C_{n, k}^{\operatorname{\mathrm{cyc}}}\left(1+ \tau^{\operatorname{\mathrm{cyc}}}\frac{1}{\displaystyle 5\prod_{\substack{\ell \mid L^{\operatorname{\mathrm{odd}}} \\ \ell \nmid n}} (|\operatorname{\mathrm{GL}}_2(\mathbb{Z}/\ell\mathbb{Z})|-1)}\right). \end{align*} $$
$$ \begin{align*} C_{E, n, k}^{\operatorname{\mathrm{cyc}}} & = \frac{|G_E(L) \cap \Psi^{\operatorname{\mathrm{cyc}}}_{n,k}(L)|}{|G_E(L)|} \prod_{\substack{\ell \nmid m_E \\ \ell^\alpha \parallel n}} \delta^{\operatorname{\mathrm{cyc}}}_{E,n,k}(\ell^\alpha) \prod_{\ell \nmid nm_E} \delta^{\operatorname{\mathrm{cyc}}}_{E}(\ell) \\ & =C_{n, k}^{\operatorname{\mathrm{cyc}}}\left(1+ \tau^{\operatorname{\mathrm{cyc}}}\frac{1}{\displaystyle 5\prod_{\substack{\ell \mid L^{\operatorname{\mathrm{odd}}} \\ \ell \nmid n}} (|\operatorname{\mathrm{GL}}_2(\mathbb{Z}/\ell\mathbb{Z})|-1)}\right). \end{align*} $$
Now we move on to the Koblitz case. By Lemma 5.4, we have
![]() $|Y^{\operatorname {\mathrm {prime}}}_{2^{\alpha },+}| - |Y^{\operatorname {\mathrm {prime}}}_{2^{\alpha },-}|=-\tau 2^{3\alpha -2}$
. Hence, by (52), a simple calculation reveals that
$|Y^{\operatorname {\mathrm {prime}}}_{2^{\alpha },+}| - |Y^{\operatorname {\mathrm {prime}}}_{2^{\alpha },-}|=-\tau 2^{3\alpha -2}$
. Hence, by (52), a simple calculation reveals that
![]() $|G_E(L) \cap \Psi ^{\operatorname {\mathrm {prime}}}_{n,k}(L)|$
equals
$|G_E(L) \cap \Psi ^{\operatorname {\mathrm {prime}}}_{n,k}(L)|$
equals
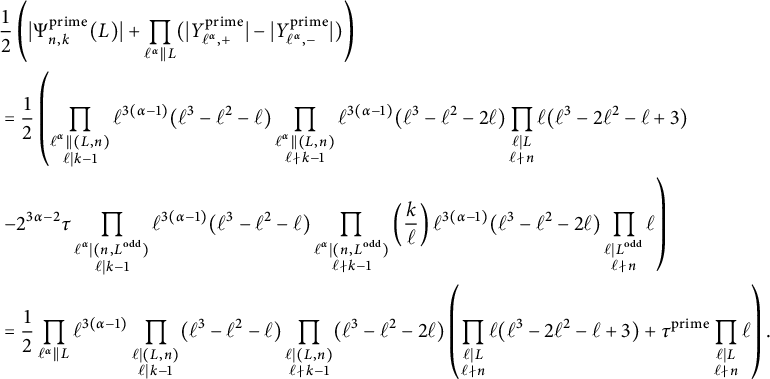 $$ \begin{align*} &\frac{1}{2}\left(|\Psi^{\operatorname{\mathrm{prime}}}_{n,k}(L)| + \prod_{\ell^\alpha \parallel L}(|Y^{\operatorname{\mathrm{prime}}}_{\ell^\alpha,+}| - |Y^{\operatorname{\mathrm{prime}}}_{\ell^\alpha,-}|) \right) \\ &= \frac{1}{2}\left( \prod_{\substack{\ell^{\alpha}\parallel (L, n)\\ \ell\mid k-1}}\ell^{3(\alpha-1)}(\ell^3-\ell^2-\ell)\prod_{\substack{\ell^{\alpha}\parallel (L, n)\\ \ell\nmid k-1}}\ell^{3(\alpha-1)}(\ell^3-\ell^2-2\ell)\prod_{\substack{\ell\mid L\\\ell \nmid n}}\ell(\ell^3-2\ell^2-\ell+3) \right. \\ &\left. - 2^{3\alpha-2} \tau \prod_{\substack{\ell^{\alpha}\mid (n, L^{\operatorname{\mathrm{odd}}})\\ \ell\mid k-1}} \ell^{3(\alpha-1)}(\ell^3-\ell^2-\ell) \prod_{\substack{\ell^{\alpha}\mid (n, L^{\operatorname{\mathrm{odd}}})\\ \ell\nmid k-1}}\left(\frac{k}{\ell}\right)\ell^{3(\alpha-1)}(\ell^3-\ell^2-2\ell) \prod_{\substack{\ell \mid L^{\operatorname{\mathrm{odd}}}\\ \ell \nmid n}} \ell \right) \\ &= \frac{1}{2} \prod_{\ell^\alpha \parallel L}\ell^{3(\alpha-1)} \prod_{\substack{\ell \mid (L,n) \\ \ell \mid k-1}}(\ell^3-\ell^2-\ell) \prod_{\substack{\ell \mid (L,n) \\ \ell \nmid k-1}}(\ell^3-\ell^2-2\ell) \left( \prod_{\substack{\ell \mid L \\ \ell \nmid n}}\ell(\ell^3-2\ell^2-\ell+3) +\tau^{\operatorname{\mathrm{prime}}} \prod_{\substack{\ell \mid L \\ \ell \nmid n}}\ell\right). \end{align*} $$
$$ \begin{align*} &\frac{1}{2}\left(|\Psi^{\operatorname{\mathrm{prime}}}_{n,k}(L)| + \prod_{\ell^\alpha \parallel L}(|Y^{\operatorname{\mathrm{prime}}}_{\ell^\alpha,+}| - |Y^{\operatorname{\mathrm{prime}}}_{\ell^\alpha,-}|) \right) \\ &= \frac{1}{2}\left( \prod_{\substack{\ell^{\alpha}\parallel (L, n)\\ \ell\mid k-1}}\ell^{3(\alpha-1)}(\ell^3-\ell^2-\ell)\prod_{\substack{\ell^{\alpha}\parallel (L, n)\\ \ell\nmid k-1}}\ell^{3(\alpha-1)}(\ell^3-\ell^2-2\ell)\prod_{\substack{\ell\mid L\\\ell \nmid n}}\ell(\ell^3-2\ell^2-\ell+3) \right. \\ &\left. - 2^{3\alpha-2} \tau \prod_{\substack{\ell^{\alpha}\mid (n, L^{\operatorname{\mathrm{odd}}})\\ \ell\mid k-1}} \ell^{3(\alpha-1)}(\ell^3-\ell^2-\ell) \prod_{\substack{\ell^{\alpha}\mid (n, L^{\operatorname{\mathrm{odd}}})\\ \ell\nmid k-1}}\left(\frac{k}{\ell}\right)\ell^{3(\alpha-1)}(\ell^3-\ell^2-2\ell) \prod_{\substack{\ell \mid L^{\operatorname{\mathrm{odd}}}\\ \ell \nmid n}} \ell \right) \\ &= \frac{1}{2} \prod_{\ell^\alpha \parallel L}\ell^{3(\alpha-1)} \prod_{\substack{\ell \mid (L,n) \\ \ell \mid k-1}}(\ell^3-\ell^2-\ell) \prod_{\substack{\ell \mid (L,n) \\ \ell \nmid k-1}}(\ell^3-\ell^2-2\ell) \left( \prod_{\substack{\ell \mid L \\ \ell \nmid n}}\ell(\ell^3-2\ell^2-\ell+3) +\tau^{\operatorname{\mathrm{prime}}} \prod_{\substack{\ell \mid L \\ \ell \nmid n}}\ell\right). \end{align*} $$
Finally, by Proposition 4.4, Lemma 4.5, (51), and (53), we get
 $$ \begin{align*} C_{E, n, k}^{\operatorname{\mathrm{prime}}} & =\frac{|G_E(L) \cap \Psi^{\operatorname{\mathrm{prime}}}_{n,k}(L)|}{|G_E(L)|\cdot \prod_{\ell \mid L}(1-1/\ell)} \prod_{\substack{\ell \nmid m_E \\ \ell^\alpha \parallel n}} \frac{\delta^{\operatorname{\mathrm{prime}}}_{E,n,k}(\ell^\alpha)}{1-1/\ell} \prod_{\ell \nmid nm_E} \frac{\delta^{\operatorname{\mathrm{prime}}}_{E}(\ell)}{1-1/\ell} \\ & = C_{n, k}^{\operatorname{\mathrm{prime}}}\left(1+ \frac{\tau^{\operatorname{\mathrm{prime}}} \cdot \displaystyle \prod_{\substack{\ell\mid L \\\ell\nmid n}}\ell}{\displaystyle \prod_{\substack{\ell\mid L \\\ell\nmid n}}\ell(\ell^3-2\ell^2-\ell+3)}\right) = C_{n, k}^{\operatorname{\mathrm{prime}}}\left(1+ \frac{\tau^{\operatorname{\mathrm{prime}}}}{\displaystyle \prod_{\substack{\ell\mid L \\\ell\nmid n}}(\ell^3-2\ell^2-\ell+3)}\right). \end{align*} $$
$$ \begin{align*} C_{E, n, k}^{\operatorname{\mathrm{prime}}} & =\frac{|G_E(L) \cap \Psi^{\operatorname{\mathrm{prime}}}_{n,k}(L)|}{|G_E(L)|\cdot \prod_{\ell \mid L}(1-1/\ell)} \prod_{\substack{\ell \nmid m_E \\ \ell^\alpha \parallel n}} \frac{\delta^{\operatorname{\mathrm{prime}}}_{E,n,k}(\ell^\alpha)}{1-1/\ell} \prod_{\ell \nmid nm_E} \frac{\delta^{\operatorname{\mathrm{prime}}}_{E}(\ell)}{1-1/\ell} \\ & = C_{n, k}^{\operatorname{\mathrm{prime}}}\left(1+ \frac{\tau^{\operatorname{\mathrm{prime}}} \cdot \displaystyle \prod_{\substack{\ell\mid L \\\ell\nmid n}}\ell}{\displaystyle \prod_{\substack{\ell\mid L \\\ell\nmid n}}\ell(\ell^3-2\ell^2-\ell+3)}\right) = C_{n, k}^{\operatorname{\mathrm{prime}}}\left(1+ \frac{\tau^{\operatorname{\mathrm{prime}}}}{\displaystyle \prod_{\substack{\ell\mid L \\\ell\nmid n}}(\ell^3-2\ell^2-\ell+3)}\right). \end{align*} $$
This completes the proof of Theorem 1.7.
6 On the Koblitz constant for non-Serre curves
6.1 Bounding the Koblitz constant for non-CM, non-Serre curves
In this subsection, we will determine an upper bound for
![]() $C^{\operatorname {\mathrm {prime}}}_{E,n,k}$
in the case of non-CM, non-Serre curves.
$C^{\operatorname {\mathrm {prime}}}_{E,n,k}$
in the case of non-CM, non-Serre curves.
Let
![]() $E/\mathbb {Q}$
be a non-CM, non-Serre curve, defined by the model (4), of adelic level
$E/\mathbb {Q}$
be a non-CM, non-Serre curve, defined by the model (4), of adelic level
![]() $m_E$
. Let L be defined as in (7). Then we write
$m_E$
. Let L be defined as in (7). Then we write
![]() $L = L_1L_2$
such that
$L = L_1L_2$
such that
![]() $L_2$
is the product of prime powers
$L_2$
is the product of prime powers
![]() $\ell ^{\alpha } \parallel L$
with
$\ell ^{\alpha } \parallel L$
with
![]() $\ell \not \in \{2,3,5\}$
and
$\ell \not \in \{2,3,5\}$
and
![]() $G_E(\ell ) \simeq \operatorname {\mathrm {GL}}_2(\mathbb {Z}/\ell \mathbb {Z})$
. By [Reference Cojocaru17, Appendix, Theorem 1],
$G_E(\ell ) \simeq \operatorname {\mathrm {GL}}_2(\mathbb {Z}/\ell \mathbb {Z})$
. By [Reference Cojocaru17, Appendix, Theorem 1],
![]() $G_E(L_2) \simeq \operatorname {\mathrm {GL}}_2(\mathbb {Z}/L_2\mathbb {Z})$
. Let
$G_E(L_2) \simeq \operatorname {\mathrm {GL}}_2(\mathbb {Z}/L_2\mathbb {Z})$
. Let
![]() $\varpi \colon \operatorname {\mathrm {GL}}_2(\mathbb {Z}/L\mathbb {Z}) \to \operatorname {\mathrm {GL}}_2(\mathbb {Z}/L_2\mathbb {Z})$
be the natural reduction map. Note that
$\varpi \colon \operatorname {\mathrm {GL}}_2(\mathbb {Z}/L\mathbb {Z}) \to \operatorname {\mathrm {GL}}_2(\mathbb {Z}/L_2\mathbb {Z})$
be the natural reduction map. Note that
Since
![]() $\varpi $
is a surjective group homomorphism, we have
$\varpi $
is a surjective group homomorphism, we have
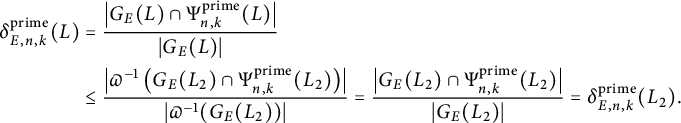 $$ \begin{align} \begin{aligned} \delta_{E,n,k}^{\operatorname{\mathrm{prime}}}(L) &= \frac{\left|G_E(L) \cap \Psi^{\operatorname{\mathrm{prime}}}_{n,k}(L)\right|}{\left|G_E(L)\right|} \\ &\leq \frac{\left| \varpi^{-1}\left(G_E(L_2) \cap \Psi^{\operatorname{\mathrm{prime}}}_{n,k}(L_2)\right)\right|}{|\varpi^{-1}(G_E(L_2))|} = \frac{\left| G_E(L_2) \cap \Psi^{\operatorname{\mathrm{prime}}}_{n,k}(L_2)\right|}{|G_E(L_2)|} = \delta_{E,n,k}^{\operatorname{\mathrm{prime}}}(L_2). \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} \delta_{E,n,k}^{\operatorname{\mathrm{prime}}}(L) &= \frac{\left|G_E(L) \cap \Psi^{\operatorname{\mathrm{prime}}}_{n,k}(L)\right|}{\left|G_E(L)\right|} \\ &\leq \frac{\left| \varpi^{-1}\left(G_E(L_2) \cap \Psi^{\operatorname{\mathrm{prime}}}_{n,k}(L_2)\right)\right|}{|\varpi^{-1}(G_E(L_2))|} = \frac{\left| G_E(L_2) \cap \Psi^{\operatorname{\mathrm{prime}}}_{n,k}(L_2)\right|}{|G_E(L_2)|} = \delta_{E,n,k}^{\operatorname{\mathrm{prime}}}(L_2). \end{aligned} \end{align} $$
Since
![]() $\rho _{E,L_2}$
is surjective, we apply the same argument as in the proof of Lemma 4.5 and obtain
$\rho _{E,L_2}$
is surjective, we apply the same argument as in the proof of Lemma 4.5 and obtain
 $$ \begin{align*}\frac{\delta_{E,n,k}^{\operatorname{\mathrm{prime}}}(L_2)}{\prod_{\ell \mid L_2}(1-1/\ell)}\leq 1.\end{align*} $$
$$ \begin{align*}\frac{\delta_{E,n,k}^{\operatorname{\mathrm{prime}}}(L_2)}{\prod_{\ell \mid L_2}(1-1/\ell)}\leq 1.\end{align*} $$
Before proceeding to bound the constant
![]() $C_{E, n, k}^{\operatorname {\mathrm {prime}}}$
, we first state a standard analytic result.
$C_{E, n, k}^{\operatorname {\mathrm {prime}}}$
, we first state a standard analytic result.
Lemma 6.1 For any positive integer M, we have
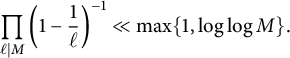 $$ \begin{align*}\prod_{\ell \mid M} \left(1-\frac{1}{\ell}\right)^{-1} \ll \max\{1, \log \log M\}.\end{align*} $$
$$ \begin{align*}\prod_{\ell \mid M} \left(1-\frac{1}{\ell}\right)^{-1} \ll \max\{1, \log \log M\}.\end{align*} $$
Proof Follows from Mertens’ theorem [Reference Mertens44, p. 53, (15)]. See [Reference Zywina62, p. 767] for the argument.
From Lemma 4.5, Lemma 6.1, (32), (36), and (54), we obtain
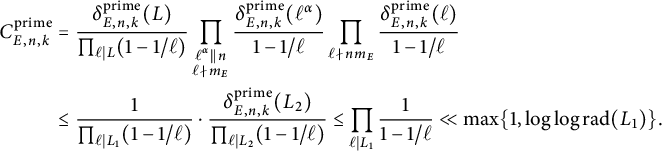 $$ \begin{align} \begin{aligned} C^{\operatorname{\mathrm{prime}}}_{E,n,k} &= \frac{\delta_{E,n,k}^{\operatorname{\mathrm{prime}}}(L)}{\prod_{\ell \mid L}(1-1/\ell)} \prod_{\substack{\ell^\alpha \parallel n \\ \ell \nmid m_E}}\frac{\delta_{E,n,k}^{\operatorname{\mathrm{prime}}}(\ell^\alpha)}{1-1/\ell} \prod_{\ell \nmid nm_E}\frac{\delta_{E,n,k}^{\operatorname{\mathrm{prime}}}(\ell)}{1-1/\ell} \\ &\leq \frac{1}{\prod_{\ell \mid L_1}(1-1/\ell)} \cdot \frac{\delta_{E,n,k}^{\operatorname{\mathrm{prime}}}(L_2)}{\prod_{\ell \mid L_2}(1-1/\ell)} \leq \prod_{\ell \mid L_1} \frac{1}{1-1/\ell} \ll \max\{1, \log \log \operatorname{\mathrm{rad}}(L_1)\}. \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} C^{\operatorname{\mathrm{prime}}}_{E,n,k} &= \frac{\delta_{E,n,k}^{\operatorname{\mathrm{prime}}}(L)}{\prod_{\ell \mid L}(1-1/\ell)} \prod_{\substack{\ell^\alpha \parallel n \\ \ell \nmid m_E}}\frac{\delta_{E,n,k}^{\operatorname{\mathrm{prime}}}(\ell^\alpha)}{1-1/\ell} \prod_{\ell \nmid nm_E}\frac{\delta_{E,n,k}^{\operatorname{\mathrm{prime}}}(\ell)}{1-1/\ell} \\ &\leq \frac{1}{\prod_{\ell \mid L_1}(1-1/\ell)} \cdot \frac{\delta_{E,n,k}^{\operatorname{\mathrm{prime}}}(L_2)}{\prod_{\ell \mid L_2}(1-1/\ell)} \leq \prod_{\ell \mid L_1} \frac{1}{1-1/\ell} \ll \max\{1, \log \log \operatorname{\mathrm{rad}}(L_1)\}. \end{aligned} \end{align} $$
Our next task is to bound
![]() $\operatorname {\mathrm {rad}} (L_1)$
in terms of a and b appearing in the short Weierstrass model (4) of E. Write
$\operatorname {\mathrm {rad}} (L_1)$
in terms of a and b appearing in the short Weierstrass model (4) of E. Write
![]() $j_E\in \mathbb {Q}$
to denote the j-invariant of E and
$j_E\in \mathbb {Q}$
to denote the j-invariant of E and ![]() for the Weil height of
for the Weil height of
![]() $j_E$
. If
$j_E$
. If
![]() $\ell \mid L_1$
, then either
$\ell \mid L_1$
, then either
![]() $\ell \leq 5$
or
$\ell \leq 5$
or
![]() $\rho _{E,\ell }$
is not surjective. By the main theorem of [Reference Masser and Wüstholz41], there exist absolute constant
$\rho _{E,\ell }$
is not surjective. By the main theorem of [Reference Masser and Wüstholz41], there exist absolute constant
![]() $\kappa $
and
$\kappa $
and
![]() $\lambda $
for which
$\lambda $
for which
![]() $\rho _{E,\ell }$
is surjective for all
$\rho _{E,\ell }$
is surjective for all
![]() $\ell> \kappa (\max \{1,h\})^\lambda $
. Since
$\ell> \kappa (\max \{1,h\})^\lambda $
. Since
![]() $\operatorname {\mathrm {rad}}(L_1)$
is squarefree, we have
$\operatorname {\mathrm {rad}}(L_1)$
is squarefree, we have
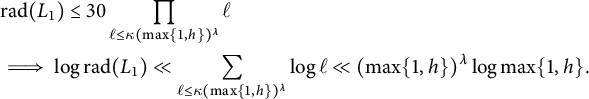 $$ \begin{align} & \operatorname{\mathrm{rad}}(L_1) \leq 30\prod_{\ell \leq \kappa (\max\{1,h\})^\lambda} \ell \nonumber \\ & \implies \log \operatorname{\mathrm{rad}} (L_1) \ll \sum_{\ell \leq \kappa(\max\{1,h\})^\lambda} \log \ell \ll (\max\{1,h\})^\lambda \log \max\{1, h\}. \end{align} $$
$$ \begin{align} & \operatorname{\mathrm{rad}}(L_1) \leq 30\prod_{\ell \leq \kappa (\max\{1,h\})^\lambda} \ell \nonumber \\ & \implies \log \operatorname{\mathrm{rad}} (L_1) \ll \sum_{\ell \leq \kappa(\max\{1,h\})^\lambda} \log \ell \ll (\max\{1,h\})^\lambda \log \max\{1, h\}. \end{align} $$
Since E is given by the model (4), we have that
Combining (55), (56), and (57), we obtain the following result.
Proposition 6.2 Let
![]() $E/\mathbb {Q}$
be a non-CM, non-Serre curve given by (4). Then we have
$E/\mathbb {Q}$
be a non-CM, non-Serre curve given by (4). Then we have
6.2 Bounding the Koblitz constant for CM curves
In this subsection, we focus on CM elliptic curves
![]() $E/\mathbb {Q}$
. The goal is to show that the constant
$E/\mathbb {Q}$
. The goal is to show that the constant
![]() $C^{\operatorname {\mathrm {prime}}}_{E, n, k}$
is bounded independent of the choice of the CM curve (Proposition 6.7). We keep the notation from Section 2.3.
$C^{\operatorname {\mathrm {prime}}}_{E, n, k}$
is bounded independent of the choice of the CM curve (Proposition 6.7). We keep the notation from Section 2.3.
Let
![]() $E/\mathbb {Q}$
be an elliptic curve with CM by an order
$E/\mathbb {Q}$
be an elliptic curve with CM by an order
![]() $\mathcal {O}$
in an imaginary quadratic field
$\mathcal {O}$
in an imaginary quadratic field
![]() $K = \mathbb {Q}(\sqrt {-D})$
. Let p be a prime of Koblitz reduction for
$K = \mathbb {Q}(\sqrt {-D})$
. Let p be a prime of Koblitz reduction for
![]() $E/\mathbb {Q}$
. Since
$E/\mathbb {Q}$
. Since
![]() $[K:\mathbb {Q}] = 2$
, the prime p either splits completely, stays inert, or ramifies over
$[K:\mathbb {Q}] = 2$
, the prime p either splits completely, stays inert, or ramifies over
![]() $K/\mathbb {Q}$
.
$K/\mathbb {Q}$
.
If p does not split over
![]() $K/\mathbb {Q}$
, then by Deuring’s criterion [Reference Deuring23], p is a supersingular prime for E and we have
$K/\mathbb {Q}$
, then by Deuring’s criterion [Reference Deuring23], p is a supersingular prime for E and we have
![]() $a_p(E) = 0$
. Therefore,
$a_p(E) = 0$
. Therefore,
which is an even number if
![]() $p> 2$
. Thus, an odd supersingular prime cannot be a prime of Koblitz reduction for E.
$p> 2$
. Thus, an odd supersingular prime cannot be a prime of Koblitz reduction for E.
Now suppose p splits completely in K and let
![]() $\mathbf {p}$
be a prime lying above p. We consider two cases depending on the value of D modulo
$\mathbf {p}$
be a prime lying above p. We consider two cases depending on the value of D modulo
![]() $4$
. Following the notation of [Reference Wan and Xi58, Chapter 2.2], when
$4$
. Following the notation of [Reference Wan and Xi58, Chapter 2.2], when
![]() $D \equiv 1,2 \ \pmod 4$
, let
$D \equiv 1,2 \ \pmod 4$
, let
![]() $M,N\in \mathbb {Z}$
be such that
$M,N\in \mathbb {Z}$
be such that
![]() $\mathbf {p}$
is generated by
$\mathbf {p}$
is generated by
![]() $M+N\sqrt {-D}$
for some
$M+N\sqrt {-D}$
for some
![]() $M,N\in \mathbb {Z}$
. In this case, the Frobenius trace satisfies
$M,N\in \mathbb {Z}$
. In this case, the Frobenius trace satisfies
![]() $a_p(E) = 2M$
, so
$a_p(E) = 2M$
, so
![]() $|\widetilde {E}_p(\mathbb {F}_p)| = p+1-a_p(E)$
is always even for odd primes p. Therefore,
$|\widetilde {E}_p(\mathbb {F}_p)| = p+1-a_p(E)$
is always even for odd primes p. Therefore,
![]() $\pi _E^{\operatorname {\mathrm {prime}}}(x)$
is uniformly bounded.
$\pi _E^{\operatorname {\mathrm {prime}}}(x)$
is uniformly bounded.
On the other hand, if
![]() $D \equiv 3 \ \pmod 4$
, then we can let
$D \equiv 3 \ \pmod 4$
, then we can let
![]() $M,N \in \mathbb {Z}$
be such that
$M,N \in \mathbb {Z}$
be such that
![]() $M + N(1+\sqrt {-D})/2$
generates
$M + N(1+\sqrt {-D})/2$
generates
![]() $\mathbf {p}$
. Let us define a binary quadratic form
$\mathbf {p}$
. Let us define a binary quadratic form
Then, one can check
Thus, we see that this is related to studying integer pairs
![]() $(M,N) \in \mathbb {Z}^2$
for which both
$(M,N) \in \mathbb {Z}^2$
for which both
![]() $f_D(M,N)$
and
$f_D(M,N)$
and
![]() $f_D(M-1,N)$
are primes. This setup is a special case of the multivariate Bateman–Horn conjecture [Reference Bateman and Horn7], which generalizes the Hardy–Littlewood conjecture to the setting of several variables [Reference Hardy and Littlewood29].
$f_D(M-1,N)$
are primes. This setup is a special case of the multivariate Bateman–Horn conjecture [Reference Bateman and Horn7], which generalizes the Hardy–Littlewood conjecture to the setting of several variables [Reference Hardy and Littlewood29].
This idea can be used to note additional CM curves for which
![]() $\pi _E^{\operatorname {\mathrm {prime}}}(x)$
is bounded. Suppose
$\pi _E^{\operatorname {\mathrm {prime}}}(x)$
is bounded. Suppose
![]() $D \equiv 7 \ \pmod 8$
. (In fact,
$D \equiv 7 \ \pmod 8$
. (In fact,
![]() $K = \mathbb {Q}(\sqrt {-7})$
is the only CM field satisfying the property.) A direct calculation shows that there are no integer pairs
$K = \mathbb {Q}(\sqrt {-7})$
is the only CM field satisfying the property.) A direct calculation shows that there are no integer pairs
![]() $(M,N)$
for which both
$(M,N)$
for which both
![]() $f_D(M,N)$
and
$f_D(M,N)$
and
![]() $f_D(M-1,N)$
are odd, and thus prime. Consequently, for this curve
$f_D(M-1,N)$
are odd, and thus prime. Consequently, for this curve
![]() $\pi _E^{\operatorname {\mathrm {prime}}}(x)$
is uniformly bounded. An alternative way to see this is to observe that every elliptic curve E with CM field
$\pi _E^{\operatorname {\mathrm {prime}}}(x)$
is uniformly bounded. An alternative way to see this is to observe that every elliptic curve E with CM field
![]() $\mathbb {Q}(\sqrt {-7})$
has torsion subgroup
$\mathbb {Q}(\sqrt {-7})$
has torsion subgroup
![]() $\mathbb {Z}/2\mathbb {Z}$
.
$\mathbb {Z}/2\mathbb {Z}$
.
We now turn to our original formulation of the prime-counting function. Note that
![]() $\mathbb {F}_p \simeq \mathbb {F}_{\mathbf {p}}$
and the
$\mathbb {F}_p \simeq \mathbb {F}_{\mathbf {p}}$
and the
![]() $\widetilde {E}_p$
is isomorphic to
$\widetilde {E}_p$
is isomorphic to
![]() $\widetilde {E}_{\mathbf {p}}$
as an elliptic curve over the base field. In particular,
$\widetilde {E}_{\mathbf {p}}$
as an elliptic curve over the base field. In particular,
Thus, we obtain
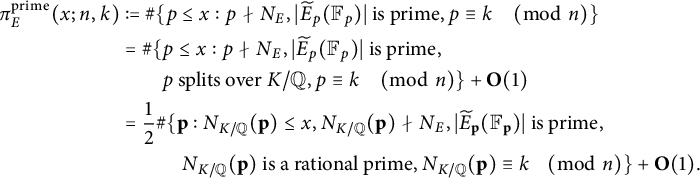
The Koblitz conjecture in arithmetic progressions for CM elliptic curves can be formulated as follows.
Conjecture 6.3 Let
![]() $E/\mathbb {Q}$
be an elliptic curve with CM by an order
$E/\mathbb {Q}$
be an elliptic curve with CM by an order
![]() $\mathcal {O}$
in an imaginary quadratic field K. Let
$\mathcal {O}$
in an imaginary quadratic field K. Let
![]() $m_E$
be as in Lemma 2.6, n be a positive integer, and k be an integer coprime to n. Then there exists a constant
$m_E$
be as in Lemma 2.6, n be a positive integer, and k be an integer coprime to n. Then there exists a constant
![]() $C^{\operatorname {\mathrm {prime}}}_{E/K,n,k}$
defined in (62) such that
$C^{\operatorname {\mathrm {prime}}}_{E/K,n,k}$
defined in (62) such that
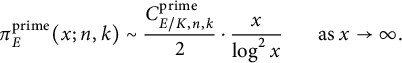 $$ \begin{align} \pi^{\operatorname{\mathrm{prime}}}_{E}(x;n,k) \sim \frac{C^{\operatorname{\mathrm{prime}}}_{E/K,n,k}}{2} \cdot \frac{x}{\log^2 x} \hspace{0.5cm} \text{ as } x\to \infty. \end{align} $$
$$ \begin{align} \pi^{\operatorname{\mathrm{prime}}}_{E}(x;n,k) \sim \frac{C^{\operatorname{\mathrm{prime}}}_{E/K,n,k}}{2} \cdot \frac{x}{\log^2 x} \hspace{0.5cm} \text{ as } x\to \infty. \end{align} $$
If the constant vanishes, we interpret (58) as stating that there are only finitely many primes
![]() $p \equiv k \ \pmod n$
of Koblitz reduction for E.
$p \equiv k \ \pmod n$
of Koblitz reduction for E.
Comparing with Conjecture 1.6, we have
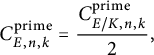 $$ \begin{align} C^{\operatorname{\mathrm{prime}}}_{E,n,k}=\frac{C^{\operatorname{\mathrm{prime}}}_{E/K,n,k}}{2}, \end{align} $$
$$ \begin{align} C^{\operatorname{\mathrm{prime}}}_{E,n,k}=\frac{C^{\operatorname{\mathrm{prime}}}_{E/K,n,k}}{2}, \end{align} $$
where
![]() $C^{\operatorname {\mathrm {prime}}}_{E/K,n,k}$
is defined in (60).
$C^{\operatorname {\mathrm {prime}}}_{E/K,n,k}$
is defined in (60).
We now introduce some notation used to determine the constant
![]() $C^{\operatorname {\mathrm {prime}}}_{E/K,n,k}$
. For a positive integer m, let us fix a
$C^{\operatorname {\mathrm {prime}}}_{E/K,n,k}$
. For a positive integer m, let us fix a
![]() $\mathbb {Z}/m\mathbb {Z}$
-basis of
$\mathbb {Z}/m\mathbb {Z}$
-basis of
![]() $\mathcal {O}/m\mathcal {O}$
. This allows us to view
$\mathcal {O}/m\mathcal {O}$
. This allows us to view
![]() $\operatorname {\mathrm {GL}}_1(\mathcal {O}/m\mathcal {O})=(\mathcal {O}/m\mathcal {O})^{\times }$
a subgroup of
$\operatorname {\mathrm {GL}}_1(\mathcal {O}/m\mathcal {O})=(\mathcal {O}/m\mathcal {O})^{\times }$
a subgroup of
![]() $\operatorname {\mathrm {GL}}_2(\mathbb {Z}/m\mathbb {Z})$
. Let
$\operatorname {\mathrm {GL}}_2(\mathbb {Z}/m\mathbb {Z})$
. Let
![]() $\operatorname {det} \colon (\mathcal {O}/m\mathcal {O})^\times \to (\mathbb {Z}/m\mathbb {Z})^\times $
be the determinant map, defined in the natural way. Fixing a standard orthogonal basis of
$\operatorname {det} \colon (\mathcal {O}/m\mathcal {O})^\times \to (\mathbb {Z}/m\mathbb {Z})^\times $
be the determinant map, defined in the natural way. Fixing a standard orthogonal basis of
![]() $\mathcal {O}/m\mathcal {O}$
, N is identified with the determinant map. Thus, drawing a parallel from (34), we are led to define
$\mathcal {O}/m\mathcal {O}$
, N is identified with the determinant map. Thus, drawing a parallel from (34), we are led to define
Observe that
![]() $\rho _{E,m}(\operatorname {\mathrm {Frob}}_{\mathbf {p}}) \in G_E(m) \cap \Psi ^{\operatorname {\mathrm {prime}}}_{K,n,k}(m)$
if and only if
$\rho _{E,m}(\operatorname {\mathrm {Frob}}_{\mathbf {p}}) \in G_E(m) \cap \Psi ^{\operatorname {\mathrm {prime}}}_{K,n,k}(m)$
if and only if
![]() $|\widetilde {E}_{\mathbf {p}}(\mathbb {F}_{\mathbf {p}})|$
is invertible in
$|\widetilde {E}_{\mathbf {p}}(\mathbb {F}_{\mathbf {p}})|$
is invertible in
![]() $\mathbb {Z}/m\mathbb {Z}$
and
$\mathbb {Z}/m\mathbb {Z}$
and
![]() $\operatorname {det}(\rho _{E,m}(\operatorname {\mathrm {Frob}}_{\mathbf {p}})) \equiv k \ \pmod {\gcd (m,n)}$
. Hence, we are led to define
$\operatorname {det}(\rho _{E,m}(\operatorname {\mathrm {Frob}}_{\mathbf {p}})) \equiv k \ \pmod {\gcd (m,n)}$
. Hence, we are led to define
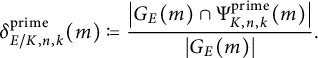
Drawing a parallel from (35), we set
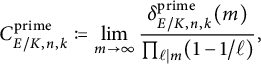
where the limit is taken over all positive integers ordered by divisibility.
Lemma 6.4 Let
![]() $E/\mathbb {Q}$
be an elliptic curve with CM by an order
$E/\mathbb {Q}$
be an elliptic curve with CM by an order
![]() $\mathcal {O}$
of conductor f in an imaginary quadratic field K. Let
$\mathcal {O}$
of conductor f in an imaginary quadratic field K. Let
![]() $m_E$
be as in Lemma 2.6. and
$m_E$
be as in Lemma 2.6. and ![]() be given as in (17). For each rational prime
be given as in (17). For each rational prime
![]() $\ell \nmid fm_E$
and
$\ell \nmid fm_E$
and
![]() $\ell \nmid n$
, we have
$\ell \nmid n$
, we have
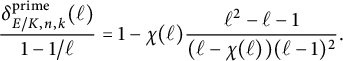 $$\begin{align*}\frac{\delta_{E/K,n,k}^{\operatorname{\mathrm{prime}}}(\ell)}{1-1/\ell}= \displaystyle 1 - \chi(\ell) \frac{\ell^2-\ell-1}{(\ell-\chi(\ell))(\ell-1)^2}. \end{align*}$$
$$\begin{align*}\frac{\delta_{E/K,n,k}^{\operatorname{\mathrm{prime}}}(\ell)}{1-1/\ell}= \displaystyle 1 - \chi(\ell) \frac{\ell^2-\ell-1}{(\ell-\chi(\ell))(\ell-1)^2}. \end{align*}$$
For each prime
![]() $\ell \nmid f m_E$
and
$\ell \nmid f m_E$
and
![]() $\ell ^{\alpha } \parallel n$
, we have
$\ell ^{\alpha } \parallel n$
, we have
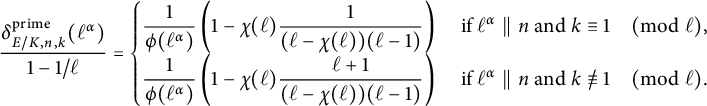 $$ \begin{align*} \frac{\delta_{E/K,n,k}^{\operatorname{\mathrm{prime}}}(\ell^{\alpha})}{1-1/\ell} = \begin{cases} \displaystyle \frac{1}{\phi(\ell^{\alpha})}\left( 1 - \chi(\ell) \frac{1}{(\ell-\chi(\ell))(\ell-1)} \right) & \text{ if } \ell^{\alpha} \parallel n \text{ and } k \equiv 1 \quad\pmod \ell, \\ \displaystyle \frac{1}{\phi(\ell^{\alpha})} \left(1 - \chi(\ell) \frac{\ell+1}{(\ell-\chi(\ell))(\ell-1)}\right) & \text{ if } \ell^{\alpha} \parallel n \text{ and } k \not \equiv 1 \quad\pmod \ell. \end{cases} \end{align*} $$
$$ \begin{align*} \frac{\delta_{E/K,n,k}^{\operatorname{\mathrm{prime}}}(\ell^{\alpha})}{1-1/\ell} = \begin{cases} \displaystyle \frac{1}{\phi(\ell^{\alpha})}\left( 1 - \chi(\ell) \frac{1}{(\ell-\chi(\ell))(\ell-1)} \right) & \text{ if } \ell^{\alpha} \parallel n \text{ and } k \equiv 1 \quad\pmod \ell, \\ \displaystyle \frac{1}{\phi(\ell^{\alpha})} \left(1 - \chi(\ell) \frac{\ell+1}{(\ell-\chi(\ell))(\ell-1)}\right) & \text{ if } \ell^{\alpha} \parallel n \text{ and } k \not \equiv 1 \quad\pmod \ell. \end{cases} \end{align*} $$
Proof First, we consider the case where
![]() $\ell \nmid nfm_E$
. By Lemma 2.6, we have
$\ell \nmid nfm_E$
. By Lemma 2.6, we have
![]() $G_E(\ell )\simeq (\mathcal {O}_K/\ell \mathcal {O}_K)^{\times }$
and the condition
$G_E(\ell )\simeq (\mathcal {O}_K/\ell \mathcal {O}_K)^{\times }$
and the condition
![]() $\operatorname {det} g\equiv k \ \pmod {\gcd (\ell , n)}$
trivially holds. Hence
$\operatorname {det} g\equiv k \ \pmod {\gcd (\ell , n)}$
trivially holds. Hence
Therefore, by Corollary 3.6, we get
depending on whether
![]() $\ell $
splits or is inert in K.
$\ell $
splits or is inert in K.
Now we assume
![]() $\ell ^{\alpha }\parallel n$
. Similarly, we have
$\ell ^{\alpha }\parallel n$
. Similarly, we have
![]() $G_E(\ell ^{\alpha })\simeq (\mathcal {O}_K/\ell ^{\alpha }\mathcal {O}_K)^{\times }$
and hence
$G_E(\ell ^{\alpha })\simeq (\mathcal {O}_K/\ell ^{\alpha }\mathcal {O}_K)^{\times }$
and hence
Then the condition
![]() $\operatorname {det} g\equiv k \ \pmod {\gcd (\ell ^{\alpha }, n)}$
becomes
$\operatorname {det} g\equiv k \ \pmod {\gcd (\ell ^{\alpha }, n)}$
becomes
![]() $\operatorname {det} g\equiv k \ \pmod {\ell ^{\alpha }}$
. So we get
$\operatorname {det} g\equiv k \ \pmod {\ell ^{\alpha }}$
. So we get
If
![]() $k\equiv 1\ \pmod \ell $
, then by Corollary 3.6,
$k\equiv 1\ \pmod \ell $
, then by Corollary 3.6,
depending on whether
![]() $\ell $
splits or is inert in K. If
$\ell $
splits or is inert in K. If
![]() $k\not \equiv 1\ \pmod \ell $
, then
$k\not \equiv 1\ \pmod \ell $
, then
depending on whether
![]() $\ell $
splits or is inert in K.
$\ell $
splits or is inert in K.
For a CM elliptic curve
![]() $E/\mathbb {Q}$
with CM by an order
$E/\mathbb {Q}$
with CM by an order
![]() $\mathcal {O}$
of conductor f, we set
$\mathcal {O}$
of conductor f, we set

To save notation, we will write
![]() $\ell ^{\alpha }$
instead of
$\ell ^{\alpha }$
instead of
![]() $\ell ^{\alpha _\ell }$
.
$\ell ^{\alpha _\ell }$
.
Proposition 6.5 Let
![]() $E/\mathbb {Q}$
have a CM by an order
$E/\mathbb {Q}$
have a CM by an order
![]() $\mathcal {O}$
of conductor f in an imaginary quadratic field K. Let
$\mathcal {O}$
of conductor f in an imaginary quadratic field K. Let ![]() be as given in (17). Let
be as given in (17). Let
![]() $m_E$
be as in Lemma 2.6. Let L be defined as in (61). Fix a positive integer n. Then,
$m_E$
be as in Lemma 2.6. Let L be defined as in (61). Fix a positive integer n. Then,
![]() $\delta ^{\operatorname {\mathrm {prime}}}_{E/K,n,k}(\cdot )$
, as an arithmetic function, satisfies the following properties:
$\delta ^{\operatorname {\mathrm {prime}}}_{E/K,n,k}(\cdot )$
, as an arithmetic function, satisfies the following properties:
-
(1) Let
 $L \mid L^{\prime } \mid L^\infty $
. Then,
$L \mid L^{\prime } \mid L^\infty $
. Then,
 $\delta ^{\operatorname {\mathrm {prime}}}_{E/K,n,k}(L) = \delta _{E/K,n,k}^{\operatorname {\mathrm {prime}}}(L^{\prime })$
;
$\delta ^{\operatorname {\mathrm {prime}}}_{E/K,n,k}(L) = \delta _{E/K,n,k}^{\operatorname {\mathrm {prime}}}(L^{\prime })$
; -
(2) Let
 $\ell ^\alpha $
be a prime power and d be a positive integer with
$\ell ^\alpha $
be a prime power and d be a positive integer with
 $(\ell , Ld) = 1$
. Then,
$(\ell , Ld) = 1$
. Then,
 $\delta ^{\operatorname {\mathrm {prime}}}_{E/K,n,k}(d\ell ^\alpha ) = \delta ^{\operatorname {\mathrm {prime}}}_{E/K,n,k}(d) \cdot \delta ^{\operatorname {\mathrm {prime}}}_{E/K,n,k}(\ell ^\alpha )$
.
$\delta ^{\operatorname {\mathrm {prime}}}_{E/K,n,k}(d\ell ^\alpha ) = \delta ^{\operatorname {\mathrm {prime}}}_{E/K,n,k}(d) \cdot \delta ^{\operatorname {\mathrm {prime}}}_{E/K,n,k}(\ell ^\alpha )$
. -
(3) Let
 $\ell ^\alpha \parallel n$
and
$\ell ^\alpha \parallel n$
and
 $(\ell , L) = 1$
. Then, for any
$(\ell , L) = 1$
. Then, for any
 $\beta> \alpha $
,
$\beta> \alpha $
,
 $\delta _{E/K,n,k}^{\operatorname {\mathrm {prime}}}(\ell ^\beta ) = \delta _{E/K,n,k}^{\operatorname {\mathrm {prime}}}(\ell ^\alpha )$
. Further, if
$\delta _{E/K,n,k}^{\operatorname {\mathrm {prime}}}(\ell ^\beta ) = \delta _{E/K,n,k}^{\operatorname {\mathrm {prime}}}(\ell ^\alpha )$
. Further, if
 $\ell \nmid nL$
, we have
$\ell \nmid nL$
, we have
 $\delta _{E/K,n,k}^{\operatorname {\mathrm {prime}}}(\ell ^\beta ) = \delta _{E/K,n,k}^{\operatorname {\mathrm {prime}}}(\ell )$
.
$\delta _{E/K,n,k}^{\operatorname {\mathrm {prime}}}(\ell ^\beta ) = \delta _{E/K,n,k}^{\operatorname {\mathrm {prime}}}(\ell )$
.
Therefore, (60) can be expressed as
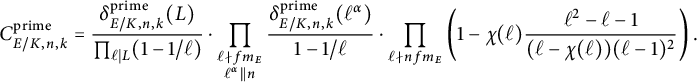 $$ \begin{align} C^{\operatorname{\mathrm{prime}}}_{E/K,n,k} = \frac{\delta_{E/K,n,k}^{\operatorname{\mathrm{prime}}}(L)}{\prod_{\ell \mid L} (1-1/\ell)} \cdot \prod_{\substack{\ell \nmid fm_E \\ \ell^{\alpha} \parallel n}}\frac{\delta_{E/K,n,k}^{\operatorname{\mathrm{prime}}}(\ell^{\alpha})}{1-1/\ell} \cdot \prod_{\substack{ \ell \nmid nfm_E}} \left(1 - \chi(\ell)\frac{\ell^2-\ell-1}{(\ell-\chi(\ell))(\ell-1)^2} \right). \end{align} $$
$$ \begin{align} C^{\operatorname{\mathrm{prime}}}_{E/K,n,k} = \frac{\delta_{E/K,n,k}^{\operatorname{\mathrm{prime}}}(L)}{\prod_{\ell \mid L} (1-1/\ell)} \cdot \prod_{\substack{\ell \nmid fm_E \\ \ell^{\alpha} \parallel n}}\frac{\delta_{E/K,n,k}^{\operatorname{\mathrm{prime}}}(\ell^{\alpha})}{1-1/\ell} \cdot \prod_{\substack{ \ell \nmid nfm_E}} \left(1 - \chi(\ell)\frac{\ell^2-\ell-1}{(\ell-\chi(\ell))(\ell-1)^2} \right). \end{align} $$
Proof One can prove (1)–(3) following the same strategy as in the proof of Proposition 4.4. One only needs to replace
![]() $m_E$
by
$m_E$
by
![]() $fm_E$
and
$fm_E$
and
![]() $\operatorname {\mathrm {GL}}_2(\mathbb {Z}/\ell ^{\alpha }\mathbb {Z})$
by
$\operatorname {\mathrm {GL}}_2(\mathbb {Z}/\ell ^{\alpha }\mathbb {Z})$
by
![]() $(\mathcal {O}/\ell ^{\alpha }\mathcal {O})^\times $
. Therefore, from these results, we get
$(\mathcal {O}/\ell ^{\alpha }\mathcal {O})^\times $
. Therefore, from these results, we get
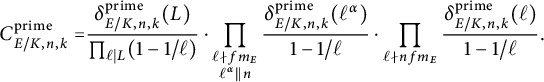 $$ \begin{align*} C^{\operatorname{\mathrm{prime}}}_{E/K,n,k} = & \frac{\delta_{E/K,n,k}^{\operatorname{\mathrm{prime}}}(L)}{\prod_{\ell \mid L} (1-1/\ell)} \cdot \prod_{\substack{\ell \nmid fm_E \\ \ell^{\alpha} \parallel n}}\frac{\delta_{E/K,n,k}^{\operatorname{\mathrm{prime}}}(\ell^{\alpha})}{1-1/\ell} \cdot \prod_{\substack{\ell \nmid nfm_E}} \frac{\delta_{E/K,n,k}^{\operatorname{\mathrm{prime}}}(\ell)}{1-1/\ell}. \end{align*} $$
$$ \begin{align*} C^{\operatorname{\mathrm{prime}}}_{E/K,n,k} = & \frac{\delta_{E/K,n,k}^{\operatorname{\mathrm{prime}}}(L)}{\prod_{\ell \mid L} (1-1/\ell)} \cdot \prod_{\substack{\ell \nmid fm_E \\ \ell^{\alpha} \parallel n}}\frac{\delta_{E/K,n,k}^{\operatorname{\mathrm{prime}}}(\ell^{\alpha})}{1-1/\ell} \cdot \prod_{\substack{\ell \nmid nfm_E}} \frac{\delta_{E/K,n,k}^{\operatorname{\mathrm{prime}}}(\ell)}{1-1/\ell}. \end{align*} $$
Remark 6.6 Given that
![]() $\ell \nmid nfm_E$
, we observe that
$\ell \nmid nfm_E$
, we observe that
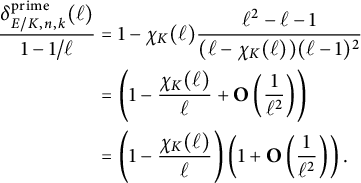 $$ \begin{align*} \frac{\delta^{\operatorname{\mathrm{prime}}}_{E/K,n,k}(\ell)}{1-1/\ell} &= 1 - \chi_K(\ell) \frac{\ell^2-\ell-1}{(\ell-\chi_K(\ell))(\ell-1)^2} \\ &= \left( 1 - \frac{\chi_K(\ell)}{\ell} + \mathbf{O}\left(\frac{1}{\ell^2}\right)\right) \\ &= \left(1 - \frac{\chi_K(\ell)}{\ell}\right)\left(1+\mathbf{O}\left(\frac{1}{\ell^2}\right)\right). \end{align*} $$
$$ \begin{align*} \frac{\delta^{\operatorname{\mathrm{prime}}}_{E/K,n,k}(\ell)}{1-1/\ell} &= 1 - \chi_K(\ell) \frac{\ell^2-\ell-1}{(\ell-\chi_K(\ell))(\ell-1)^2} \\ &= \left( 1 - \frac{\chi_K(\ell)}{\ell} + \mathbf{O}\left(\frac{1}{\ell^2}\right)\right) \\ &= \left(1 - \frac{\chi_K(\ell)}{\ell}\right)\left(1+\mathbf{O}\left(\frac{1}{\ell^2}\right)\right). \end{align*} $$
Thus, we have
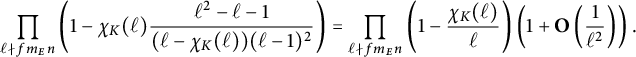 $$ \begin{align*} \prod_{\substack{\ell \nmid fm_En}} \left( 1 - \chi_K(\ell) \frac{\ell^2-\ell-1}{(\ell-\chi_K(\ell))(\ell-1)^2}\right) = \prod_{\substack{ \ell \nmid fm_En}} \left(1-\frac{\chi_K(\ell)}{\ell}\right)\left(1+\mathbf{O}\left(\frac{1}{\ell^2}\right)\right). \end{align*} $$
$$ \begin{align*} \prod_{\substack{\ell \nmid fm_En}} \left( 1 - \chi_K(\ell) \frac{\ell^2-\ell-1}{(\ell-\chi_K(\ell))(\ell-1)^2}\right) = \prod_{\substack{ \ell \nmid fm_En}} \left(1-\frac{\chi_K(\ell)}{\ell}\right)\left(1+\mathbf{O}\left(\frac{1}{\ell^2}\right)\right). \end{align*} $$
Note that this is a product of an Euler factorization of
![]() $L(s,\chi _K)^{-1}$
at
$L(s,\chi _K)^{-1}$
at
![]() $s = 1$
(with some correction factor) and an absolutely convergent product. Since
$s = 1$
(with some correction factor) and an absolutely convergent product. Since
![]() $L(1,\chi _K) \neq 0$
for a non-trivial character
$L(1,\chi _K) \neq 0$
for a non-trivial character
![]() $\chi _K$
, the infinite product in (62) is conditionally convergent.
$\chi _K$
, the infinite product in (62) is conditionally convergent.
By (58), (59), Lemma 6.4, and Proposition 6.5, we can explicitly formulate the conjectural Koblitz constant for CM elliptic curves. Let
![]() $n = n_1n_2$
where
$n = n_1n_2$
where
![]() $n_1 \mid (fm_E)^\infty $
and
$n_1 \mid (fm_E)^\infty $
and
![]() $(n_2,fm_E) = 1$
. (In particular,
$(n_2,fm_E) = 1$
. (In particular,
![]() $n_2$
is the product of
$n_2$
is the product of
![]() $\ell ^{\alpha }$
for which
$\ell ^{\alpha }$
for which
![]() $\ell ^{\alpha } \parallel n$
with
$\ell ^{\alpha } \parallel n$
with
![]() $\ell \nmid L$
.) We have
$\ell \nmid L$
.) We have
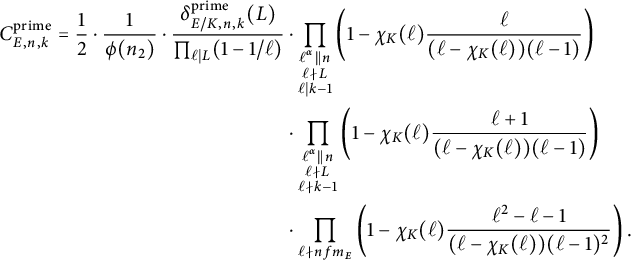 $$ \begin{align} \begin{aligned} C_{E,n,k}^{\operatorname{\mathrm{prime}}} = \frac{1}{2} \cdot \frac{1}{\phi(n_2)} \cdot \frac{\delta_{E/K, n,k}^{\operatorname{\mathrm{prime}}}(L)}{\prod_{\ell \mid L}(1-1/\ell)} & \cdot \prod_{\substack{\ell^{\alpha} \parallel n \\ \ell \nmid L \\ \ell\mid k-1}} \left( 1 - \chi_K(\ell) \frac{\ell}{(\ell-\chi_K(\ell))(\ell-1)}\right) \\ &\cdot \prod_{\substack{\ell^{\alpha} \parallel n \\ \ell \nmid L \\ \ell\nmid k-1}} \left(1-\chi_K(\ell) \frac{\ell+1}{(\ell-\chi_K(\ell))(\ell-1)}\right) \\ &\cdot \prod_{\ell \nmid nfm_E}\left(1-\chi_K(\ell)\frac{\ell^2-\ell-1}{(\ell-\chi_K(\ell))(\ell-1)^2}\right). \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} C_{E,n,k}^{\operatorname{\mathrm{prime}}} = \frac{1}{2} \cdot \frac{1}{\phi(n_2)} \cdot \frac{\delta_{E/K, n,k}^{\operatorname{\mathrm{prime}}}(L)}{\prod_{\ell \mid L}(1-1/\ell)} & \cdot \prod_{\substack{\ell^{\alpha} \parallel n \\ \ell \nmid L \\ \ell\mid k-1}} \left( 1 - \chi_K(\ell) \frac{\ell}{(\ell-\chi_K(\ell))(\ell-1)}\right) \\ &\cdot \prod_{\substack{\ell^{\alpha} \parallel n \\ \ell \nmid L \\ \ell\nmid k-1}} \left(1-\chi_K(\ell) \frac{\ell+1}{(\ell-\chi_K(\ell))(\ell-1)}\right) \\ &\cdot \prod_{\ell \nmid nfm_E}\left(1-\chi_K(\ell)\frac{\ell^2-\ell-1}{(\ell-\chi_K(\ell))(\ell-1)^2}\right). \end{aligned} \end{align} $$
Proposition 6.7 For any CM elliptic curve
![]() $E/\mathbb {Q}$
, we have
$E/\mathbb {Q}$
, we have
Proof Note that the finite product terms in (63) are all bounded by
![]() $1$
. By definition, we have
$1$
. By definition, we have
and hence,
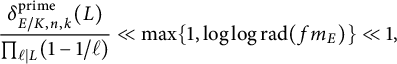 $$ \begin{align*}\frac{\delta_{E/K,n,k}^{\operatorname{\mathrm{prime}}}(L)}{\prod_{\ell \mid L}(1-1/\ell)} \ll \max\{1, \log \log \operatorname{\mathrm{rad}}(fm_E)\} \ll 1,\end{align*} $$
$$ \begin{align*}\frac{\delta_{E/K,n,k}^{\operatorname{\mathrm{prime}}}(L)}{\prod_{\ell \mid L}(1-1/\ell)} \ll \max\{1, \log \log \operatorname{\mathrm{rad}}(fm_E)\} \ll 1,\end{align*} $$
by Proposition 2.8 and Lemma 6.1. Finally, the infinite product, up to a correction factor depending on n, is universally bounded, since there are only finitely many possibilities for K.
7 Moments
The goal of this section is to complete the proof of Theorem 1.9. We begin by setting forth the general strategy. Let
![]() $x> 0$
and
$x> 0$
and
![]() $A = A(x)$
and
$A = A(x)$
and
![]() $B = B(x)$
be positive real-valued functions such that
$B = B(x)$
be positive real-valued functions such that
![]() $A(x) \to \infty $
and
$A(x) \to \infty $
and
![]() $B(x) \to \infty $
as
$B(x) \to \infty $
as
![]() $x \to \infty $
. Let
$x \to \infty $
. Let
![]() $\mathbb {E}^{a,b}$
be an elliptic curve given by the model
$\mathbb {E}^{a,b}$
be an elliptic curve given by the model
for some
![]() $a,b \in \mathbb {Z}$
and
$a,b \in \mathbb {Z}$
and
![]() $4a^3+27b^2 \neq 0$
. Define
$4a^3+27b^2 \neq 0$
. Define
Our objective is to compute, for any positive integer t, the tth moment
where
![]() $\mathcal {X}$
denotes either “
$\mathcal {X}$
denotes either “
![]() $\operatorname {\mathrm {cyc}}$
” or “
$\operatorname {\mathrm {cyc}}$
” or “
![]() $\operatorname {\mathrm {prime}}$
.” We know that (64) can be expressed as
$\operatorname {\mathrm {prime}}$
.” We know that (64) can be expressed as
 $$ \begin{align*} \frac{1}{\mathcal{|F|}} \left( \sum_{\substack{E \in \mathcal{F} \\ E \text{ is Serre}}} \left|C^{\mathcal{X}}_{E,n,k} - C^{\mathcal{X}}_{n,k}\right|{}^t + \sum_{\substack{E \in \mathcal{F} \\ E \text{ is non-CM} \nonumber \\ E \text{ is non-Serre}}} \left|C^{\mathcal{X}}_{E,n,k} - C^{\mathcal{X}}_{n,k}\right|{}^t + \sum_{\substack{E \in \mathcal{F} \\ E \text{ is CM}}} \left|C^{\mathcal{X}}_{E,n,k} - C^{\mathcal{X}}_{n,k}\right|{}^t \right), \end{align*} $$
$$ \begin{align*} \frac{1}{\mathcal{|F|}} \left( \sum_{\substack{E \in \mathcal{F} \\ E \text{ is Serre}}} \left|C^{\mathcal{X}}_{E,n,k} - C^{\mathcal{X}}_{n,k}\right|{}^t + \sum_{\substack{E \in \mathcal{F} \\ E \text{ is non-CM} \nonumber \\ E \text{ is non-Serre}}} \left|C^{\mathcal{X}}_{E,n,k} - C^{\mathcal{X}}_{n,k}\right|{}^t + \sum_{\substack{E \in \mathcal{F} \\ E \text{ is CM}}} \left|C^{\mathcal{X}}_{E,n,k} - C^{\mathcal{X}}_{n,k}\right|{}^t \right), \end{align*} $$
where “E is Serre” indicates that “E is a Serre curve,” etc. In order to bound (64), we are going to bound each of the three sums separately.
For the first sum, recall that we proved explicit formulas for the constants
![]() $C^{\mathcal {X}}_{E,n,k}$
for Serre curves in Section 5 and found that these constants closely align with their average counterparts
$C^{\mathcal {X}}_{E,n,k}$
for Serre curves in Section 5 and found that these constants closely align with their average counterparts
![]() $C^{\mathcal {X}}_{n,k}$
. For the second and third sums, we will use the fact due to Jones [Reference Jones32] that non-Serre curves are rare. For the cyclicity case, we will use the fact that
$C^{\mathcal {X}}_{n,k}$
. For the second and third sums, we will use the fact due to Jones [Reference Jones32] that non-Serre curves are rare. For the cyclicity case, we will use the fact that
![]() $C^{\operatorname {\mathrm {cyc}}}_{E,n,k}$
is bounded above by
$C^{\operatorname {\mathrm {cyc}}}_{E,n,k}$
is bounded above by
![]() $1/\phi (n)$
, which follows from (48) (and is sensible, since under GRH,
$1/\phi (n)$
, which follows from (48) (and is sensible, since under GRH,
![]() $C^{\operatorname {\mathrm {cyc}}}_{E,n,k}$
describes the density of some subset of the primes congruent to k modulo n). However, for the Koblitz case it is not clear that
$C^{\operatorname {\mathrm {cyc}}}_{E,n,k}$
describes the density of some subset of the primes congruent to k modulo n). However, for the Koblitz case it is not clear that
![]() $C^{\operatorname {\mathrm {prime}}}_{E,n,k}$
should be bounded by a constant independent of E, so we will instead employ the bounds of Propositions 6.2 and 6.7.
$C^{\operatorname {\mathrm {prime}}}_{E,n,k}$
should be bounded by a constant independent of E, so we will instead employ the bounds of Propositions 6.2 and 6.7.
We first deal with the moments computation for Serre curves. Let
![]() $\mathbb {E}^{a,b}/\mathbb {Q}$
be a Serre curve defined by the model
$\mathbb {E}^{a,b}/\mathbb {Q}$
be a Serre curve defined by the model
of adelic level
![]() $m_{\mathbb {E}^{a,b}}$
. Let
$m_{\mathbb {E}^{a,b}}$
. Let
![]() $\Delta _{a,b}'$
denote the squarefree part of the discriminant of
$\Delta _{a,b}'$
denote the squarefree part of the discriminant of
![]() $\mathbb {E}^{a,b}$
. Recall that
$\mathbb {E}^{a,b}$
. Recall that
![]() $m_{\mathbb {E}^{a,b}}$
is only supported by
$m_{\mathbb {E}^{a,b}}$
is only supported by
![]() $2$
and the prime factors of
$2$
and the prime factors of
![]() $\Delta ^{\prime }_{a,b}$
(see Proposition (2.4)). Set
$\Delta ^{\prime }_{a,b}$
(see Proposition (2.4)). Set
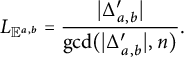 $$ \begin{align*}L_{\mathbb{E}^{a,b}} = \frac{|\Delta^{\prime}_{a,b}|}{\gcd(|\Delta^{\prime}_{a,b}|,n)}.\end{align*} $$
$$ \begin{align*}L_{\mathbb{E}^{a,b}} = \frac{|\Delta^{\prime}_{a,b}|}{\gcd(|\Delta^{\prime}_{a,b}|,n)}.\end{align*} $$
By Theorem 1.7, we have
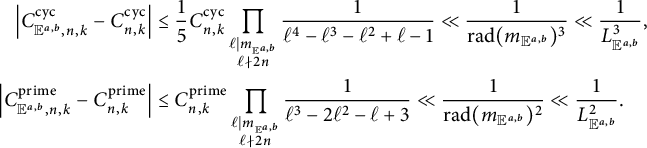 $$ \begin{align*} \left|C^{\operatorname{\mathrm{cyc}}}_{\mathbb{E}^{a,b},n,k} - C^{\operatorname{\mathrm{cyc}}}_{n,k}\right| &\leq \frac{1}{5} C^{\operatorname{\mathrm{cyc}}}_{n,k} \prod_{\substack{\ell \mid m_{\mathbb{E}^{a,b}} \\ \ell \nmid 2n}} \frac{1}{\ell^4-\ell^3-\ell^2+\ell-1} \ll \frac{1}{\operatorname{\mathrm{rad}}(m_{\mathbb{E}^{a,b}})^3} \ll \frac{1}{L_{\mathbb{E}^{a,b}}^3}, \\ \left|C^{\operatorname{\mathrm{prime}}}_{\mathbb{E}^{a,b},n,k} - C^{\operatorname{\mathrm{prime}}}_{n,k}\right| &\leq C^{\operatorname{\mathrm{prime}}}_{n,k} \prod_{\substack{\ell \mid m_{\mathbb{E}^{a,b}} \\ \ell \nmid 2n}} \frac{1}{\ell^3-2\ell^2-\ell+3} \ll \frac{1}{\operatorname{\mathrm{rad}}(m_{\mathbb{E}^{a,b}})^2} \ll \frac{1}{L_{\mathbb{E}^{a,b}}^2}. \end{align*} $$
$$ \begin{align*} \left|C^{\operatorname{\mathrm{cyc}}}_{\mathbb{E}^{a,b},n,k} - C^{\operatorname{\mathrm{cyc}}}_{n,k}\right| &\leq \frac{1}{5} C^{\operatorname{\mathrm{cyc}}}_{n,k} \prod_{\substack{\ell \mid m_{\mathbb{E}^{a,b}} \\ \ell \nmid 2n}} \frac{1}{\ell^4-\ell^3-\ell^2+\ell-1} \ll \frac{1}{\operatorname{\mathrm{rad}}(m_{\mathbb{E}^{a,b}})^3} \ll \frac{1}{L_{\mathbb{E}^{a,b}}^3}, \\ \left|C^{\operatorname{\mathrm{prime}}}_{\mathbb{E}^{a,b},n,k} - C^{\operatorname{\mathrm{prime}}}_{n,k}\right| &\leq C^{\operatorname{\mathrm{prime}}}_{n,k} \prod_{\substack{\ell \mid m_{\mathbb{E}^{a,b}} \\ \ell \nmid 2n}} \frac{1}{\ell^3-2\ell^2-\ell+3} \ll \frac{1}{\operatorname{\mathrm{rad}}(m_{\mathbb{E}^{a,b}})^2} \ll \frac{1}{L_{\mathbb{E}^{a,b}}^2}. \end{align*} $$
Let us set
![]() $r_{\operatorname {\mathrm {cyc}}} = 3$
and
$r_{\operatorname {\mathrm {cyc}}} = 3$
and
![]() $r_{\operatorname {\mathrm {prime}}} = 2$
. Then, we obtain
$r_{\operatorname {\mathrm {prime}}} = 2$
. Then, we obtain
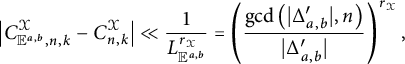 $$ \begin{align*}\left|C^{\mathcal{X}}_{\mathbb{E}^{a,b},n,k} - C^{\mathcal{X}}_{n,k}\right| \ll \frac{1}{L_{\mathbb{E}^{a,b}}^{r_{\mathcal{X}}}} = \left(\frac{\gcd\left(|\Delta^{\prime}_{a,b}|,n\right)}{|\Delta^{\prime}_{a,b}|}\right)^{r_{\mathcal{X}}},\end{align*} $$
$$ \begin{align*}\left|C^{\mathcal{X}}_{\mathbb{E}^{a,b},n,k} - C^{\mathcal{X}}_{n,k}\right| \ll \frac{1}{L_{\mathbb{E}^{a,b}}^{r_{\mathcal{X}}}} = \left(\frac{\gcd\left(|\Delta^{\prime}_{a,b}|,n\right)}{|\Delta^{\prime}_{a,b}|}\right)^{r_{\mathcal{X}}},\end{align*} $$
given that
![]() $\mathbb {E}^{a,b}/\mathbb {Q}$
is a Serre curve.
$\mathbb {E}^{a,b}/\mathbb {Q}$
is a Serre curve.
Observing that
![]() $|\mathcal {F}| \sim 4AB$
as
$|\mathcal {F}| \sim 4AB$
as
![]() $x\to \infty $
, we have for any
$x\to \infty $
, we have for any
![]() $A,B,Z \geq 2$
and
$A,B,Z \geq 2$
and
![]() $t\geq 1$
,
$t\geq 1$
,
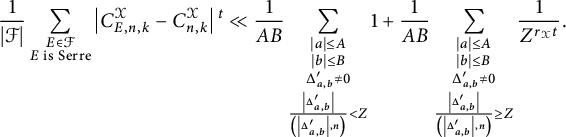 $$ \begin{align} \frac{1}{|\mathcal{F}|} \sum_{\substack{E \in \mathcal{F} \\ E \text{ is Serre}}} \left|C^{\mathcal{X}}_{E,n,k} - C^{\mathcal{X}}_{n,k}\right|{}^t \ll \frac{1}{AB} \sum_{\substack{|a|\leq A \\ |b| \leq B\\ \Delta^{\prime}_{a,b} \neq 0 \\ \frac{\left|\Delta^{\prime}_{a,b}\right|}{\left(\left|\Delta^{\prime}_{a,b}\right|,n\right)} < Z}} 1 + \frac{1}{AB} \sum_{\substack{|a|\leq A \\ |b| \leq B\\ \Delta^{\prime}_{a,b} \neq 0 \\ \frac{\left|\Delta^{\prime}_{a,b}\right|}{\left(\left|\Delta^{\prime}_{a,b}\right|,n\right)} \geq Z}} \frac{1}{Z^{r_{\mathcal{X}}t}}. \end{align} $$
$$ \begin{align} \frac{1}{|\mathcal{F}|} \sum_{\substack{E \in \mathcal{F} \\ E \text{ is Serre}}} \left|C^{\mathcal{X}}_{E,n,k} - C^{\mathcal{X}}_{n,k}\right|{}^t \ll \frac{1}{AB} \sum_{\substack{|a|\leq A \\ |b| \leq B\\ \Delta^{\prime}_{a,b} \neq 0 \\ \frac{\left|\Delta^{\prime}_{a,b}\right|}{\left(\left|\Delta^{\prime}_{a,b}\right|,n\right)} < Z}} 1 + \frac{1}{AB} \sum_{\substack{|a|\leq A \\ |b| \leq B\\ \Delta^{\prime}_{a,b} \neq 0 \\ \frac{\left|\Delta^{\prime}_{a,b}\right|}{\left(\left|\Delta^{\prime}_{a,b}\right|,n\right)} \geq Z}} \frac{1}{Z^{r_{\mathcal{X}}t}}. \end{align} $$
Lemma 7.1 With the notation above, we have
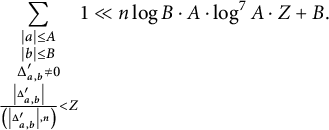 $$ \begin{align*}\sum_{\substack{|a| \leq A \\ |b| \leq B \\ \Delta^{\prime}_{a,b} \neq 0 \\ \frac{\left|\Delta^{\prime}_{a,b}\right|}{\left(\left|\Delta^{\prime}_{a,b}\right|,n\right)} < Z}} 1 \ll n\log B \cdot A \cdot \log^7 A \cdot Z + B.\end{align*} $$
$$ \begin{align*}\sum_{\substack{|a| \leq A \\ |b| \leq B \\ \Delta^{\prime}_{a,b} \neq 0 \\ \frac{\left|\Delta^{\prime}_{a,b}\right|}{\left(\left|\Delta^{\prime}_{a,b}\right|,n\right)} < Z}} 1 \ll n\log B \cdot A \cdot \log^7 A \cdot Z + B.\end{align*} $$
Proof It follows similarly to the argument given in [Reference Jones31, Section 4.2].
Let
![]() $Z = \left (B/n \log B \log ^7A \right )^{1/(r_{\mathcal {X}}t+1)}$
. By (65) and Lemma 7.1, we see that
$Z = \left (B/n \log B \log ^7A \right )^{1/(r_{\mathcal {X}}t+1)}$
. By (65) and Lemma 7.1, we see that
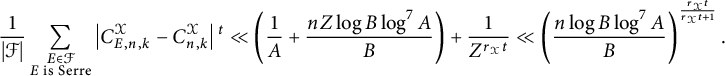 $$ \begin{align} \frac{1}{|\mathcal{F}|} \sum_{\substack{E \in \mathcal{F} \\ E \text{ is Serre}}} \left|C^{\mathcal{X}}_{E,n,k} - C^{\mathcal{X}}_{n,k}\right|{}^t \ll \left(\frac{1}{A} + \frac{n Z \log B \log^7 A}{B}\right) + \frac{1}{Z^{r_{\mathcal{X}}t}} \ll \left(\frac{n \log B \log^7A}{B} \right)^{\frac{r_{\mathcal{X}}t}{r_{\mathcal{X}}t+1}}. \end{align} $$
$$ \begin{align} \frac{1}{|\mathcal{F}|} \sum_{\substack{E \in \mathcal{F} \\ E \text{ is Serre}}} \left|C^{\mathcal{X}}_{E,n,k} - C^{\mathcal{X}}_{n,k}\right|{}^t \ll \left(\frac{1}{A} + \frac{n Z \log B \log^7 A}{B}\right) + \frac{1}{Z^{r_{\mathcal{X}}t}} \ll \left(\frac{n \log B \log^7A}{B} \right)^{\frac{r_{\mathcal{X}}t}{r_{\mathcal{X}}t+1}}. \end{align} $$
By [Reference Jones31, Theorem 25] and (66), there exists
![]() $\gamma> 0$
such that for any positive integer t,
$\gamma> 0$
such that for any positive integer t,
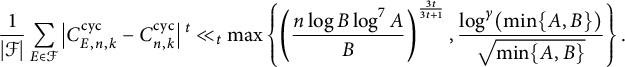 $$ \begin{align*}\frac{1}{\mathcal{|F|}} \sum_{E \in \mathcal{F}}\left|C^{\operatorname{\mathrm{cyc}}}_{E,n,k}-C^{\operatorname{\mathrm{cyc}}}_{n,k}\right|{}^t \ll_t \max \left\{\left(\frac{n\log B \log^7A}{B}\right)^{\frac{3t}{3t+1}}, \frac{\log^\gamma(\min \{A,B\})}{\sqrt{\min\{A,B\}}} \right\}.\end{align*} $$
$$ \begin{align*}\frac{1}{\mathcal{|F|}} \sum_{E \in \mathcal{F}}\left|C^{\operatorname{\mathrm{cyc}}}_{E,n,k}-C^{\operatorname{\mathrm{cyc}}}_{n,k}\right|{}^t \ll_t \max \left\{\left(\frac{n\log B \log^7A}{B}\right)^{\frac{3t}{3t+1}}, \frac{\log^\gamma(\min \{A,B\})}{\sqrt{\min\{A,B\}}} \right\}.\end{align*} $$
This completes the proof for the cyclicity case.
For primes of Koblitz reduction, by Propositions 6.2 6.7 and [Reference Jones31, Theorem 25], there exists
![]() $\gamma> 0$
such that for any positive integer t,
$\gamma> 0$
such that for any positive integer t,
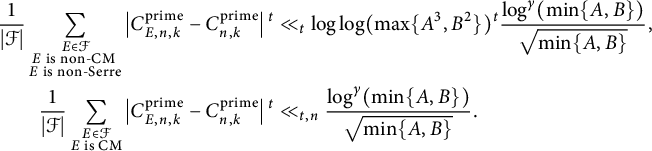 $$ \begin{align*} \frac{1}{|\mathcal{F}|} \sum_{\substack{E \in \mathcal{F} \\ E \text{ is non-CM } \\ E \text{ is non-Serre}}} \left|C_{E,n,k}^{\operatorname{\mathrm{prime}}} - C_{n,k}^{\operatorname{\mathrm{prime}}}\right|{}^t &\ll_t \log \log (\max\{A^3,B^2\})^t \frac{\log^\gamma(\min\{A,B\})}{\sqrt{\min\{A,B\}}},\\ \frac{1}{|\mathcal{F}|} \sum_{\substack{E \in \mathcal{F} \\ E \text{ is CM}}} \left| C^{\operatorname{\mathrm{prime}}}_{E,n,k} - C^{\operatorname{\mathrm{prime}}}_{n,k} \right|{}^t &\ll_{t,n} \frac{\log^\gamma(\min\{A,B\})}{\sqrt{\min\{A,B\}}}. \end{align*} $$
$$ \begin{align*} \frac{1}{|\mathcal{F}|} \sum_{\substack{E \in \mathcal{F} \\ E \text{ is non-CM } \\ E \text{ is non-Serre}}} \left|C_{E,n,k}^{\operatorname{\mathrm{prime}}} - C_{n,k}^{\operatorname{\mathrm{prime}}}\right|{}^t &\ll_t \log \log (\max\{A^3,B^2\})^t \frac{\log^\gamma(\min\{A,B\})}{\sqrt{\min\{A,B\}}},\\ \frac{1}{|\mathcal{F}|} \sum_{\substack{E \in \mathcal{F} \\ E \text{ is CM}}} \left| C^{\operatorname{\mathrm{prime}}}_{E,n,k} - C^{\operatorname{\mathrm{prime}}}_{n,k} \right|{}^t &\ll_{t,n} \frac{\log^\gamma(\min\{A,B\})}{\sqrt{\min\{A,B\}}}. \end{align*} $$
Therefore, we obtain the inequality claimed in the statement of Theorem 1.9.
8 Numerical examples
8.1 Example 1
Let E be the elliptic curve with LMFDB [53] label 1728.w1, which is given by
From the curve’s LMFDB page, we note that it is a Serre curve with adelic level
![]() $m_E = 6$
. Zywina [Reference Zywina62, Section 5] computed the Koblitz constant of E,
$m_E = 6$
. Zywina [Reference Zywina62, Section 5] computed the Koblitz constant of E,
Running either our Magma functions KoblitzAP or SerreCurveKoblitzAP [Reference Lee, Mayle and Wang39] on E with modulus
![]() $n = 6$
, we find that
$n = 6$
, we find that
This result can be verified “manually” by studying the mod
![]() $6$
Galois image of E, as we now discuss.
$6$
Galois image of E, as we now discuss.
The mod
![]() $6$
Galois image
$6$
Galois image
![]() $G_E(6)$
is an index
$G_E(6)$
is an index
![]() $2$
subgroup of
$2$
subgroup of
![]() $\operatorname {\mathrm {GL}}_2(\mathbb {Z}/6\mathbb {Z})$
generated by
$\operatorname {\mathrm {GL}}_2(\mathbb {Z}/6\mathbb {Z})$
generated by
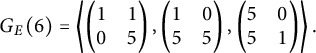 $$\begin{align*}G_E(6) = \left\langle \begin{pmatrix} 1 & 1 \\ 0 & 5 \end{pmatrix}, \begin{pmatrix} 1 & 0 \\ 5 & 5 \end{pmatrix}, \begin{pmatrix} 5 & 0 \\ 5 & 1 \end{pmatrix} \right\rangle. \end{align*}$$
$$\begin{align*}G_E(6) = \left\langle \begin{pmatrix} 1 & 1 \\ 0 & 5 \end{pmatrix}, \begin{pmatrix} 1 & 0 \\ 5 & 5 \end{pmatrix}, \begin{pmatrix} 5 & 0 \\ 5 & 1 \end{pmatrix} \right\rangle. \end{align*}$$
From this description, we compute that
Thus, if p is a good prime for E that is congruent to
![]() $5$
modulo
$5$
modulo
![]() $6$
, then
$6$
, then
Hence
![]() $|\widetilde {E}_p(\mathbb {F}_p)|$
is even for all good primes p congruent to
$|\widetilde {E}_p(\mathbb {F}_p)|$
is even for all good primes p congruent to
![]() $5$
modulo
$5$
modulo
![]() $6$
. By Hasse’s bound and computing a few values of
$6$
. By Hasse’s bound and computing a few values of
![]() $|\widetilde {E}_p(\mathbb {F}_p)|$
, we find that
$|\widetilde {E}_p(\mathbb {F}_p)|$
, we find that
![]() $|\widetilde {E}_p(\mathbb {F}_p)|$
is never
$|\widetilde {E}_p(\mathbb {F}_p)|$
is never
![]() $2$
for such primes p. Thus, the only good primes p for which
$2$
for such primes p. Thus, the only good primes p for which
![]() $|\widetilde {E}_p(\mathbb {F}_p)|$
is prime are congruent to
$|\widetilde {E}_p(\mathbb {F}_p)|$
is prime are congruent to
![]() $1$
modulo
$1$
modulo
![]() $6$
.
$6$
.
8.2 Example 2
Let E be the elliptic curve with LMFDB label 200.e1, which is given by
From this curve’s LMFDB page, we learn that E is a Serre curve with adelic level
![]() $m_E = 8$
. Running our Magma function SerreCurveKoblitzAP on E with
$m_E = 8$
. Running our Magma function SerreCurveKoblitzAP on E with
![]() $n = 8$
, we find that
$n = 8$
, we find that
where
Running our Magma function SerreCurveCyclicityAP on E with
![]() $n = 8$
, we find that
$n = 8$
, we find that
where
The values obtained above align well with numerical data for the curve. Among all primes of Koblitz reduction for E up to
![]() $10^7$
,
$10^7$
,
![]() $11114$
are congruent to
$11114$
are congruent to
![]() $1$
modulo
$1$
modulo
![]() $8$
and
$8$
and
![]() $11259$
are congruent to
$11259$
are congruent to
![]() $3$
modulo
$3$
modulo
![]() $8$
; none are congruent to
$8$
; none are congruent to
![]() $5$
or
$5$
or
![]() $7$
modulo
$7$
modulo
![]() $8$
. Among all primes of cyclic reduction for E up to
$8$
. Among all primes of cyclic reduction for E up to
![]() $10^7$
,
$10^7$
,
![]() $108096$
are congruent to
$108096$
are congruent to
![]() $1$
modulo
$1$
modulo
![]() $8$
,
$8$
,
![]() $108251$
are congruent to
$108251$
are congruent to
![]() $3$
modulo
$3$
modulo
![]() $8$
,
$8$
,
![]() $162234$
are congruent to
$162234$
are congruent to
![]() $5$
modulo
$5$
modulo
![]() $8$
, and
$8$
, and
![]() $162286$
are congruent to
$162286$
are congruent to
![]() $7$
modulo
$7$
modulo
![]() $8$
.
$8$
.
8.3 Example 3
Let E be the elliptic curve with LMFDB label 864.a1, which is given by
This curve does not have complex multiplication and is not a Serre curve. Its adelic index is
![]() $24$
and adelic level is
$24$
and adelic level is
![]() $m_E = 12$
. Running our Magma function KoblitzAP on E with
$m_E = 12$
. Running our Magma function KoblitzAP on E with
![]() $n = 12$
, we find that
$n = 12$
, we find that
where
Running our Magma function CyclicityAP on E with
![]() $n = 12$
, we find that
$n = 12$
, we find that
where
As with the previous example, these values agree well with the numerical data for the curve, which is available through our GitHub repository [Reference Lee, Mayle and Wang39].
8.4 Example 4
Let
![]() $n=6$
and E be the CM elliptic curve with LMFDB label 432.d1 defined by
$n=6$
and E be the CM elliptic curve with LMFDB label 432.d1 defined by
We keep the notation from Section 2.3. From the LMFDB, we know that
-
(1) E has CM by the maximal order
 $\mathcal {O} =\mathbb {Z}\left [\frac {1+\sqrt {-3}}{2}\right ]$
of the CM field
$\mathcal {O} =\mathbb {Z}\left [\frac {1+\sqrt {-3}}{2}\right ]$
of the CM field
 $K = \mathbb {Q}(\sqrt {-3})$
.
$K = \mathbb {Q}(\sqrt {-3})$
. -
(2) E has discriminant
 $\Delta _E=- 2^{8} 3^{3}$
. So 2 and 3 are the only primes of bad reduction for E.
$\Delta _E=- 2^{8} 3^{3}$
. So 2 and 3 are the only primes of bad reduction for E. -
(3) The map
is surjective for all primes $$\begin{align*}\rho_{E, \ell} : \operatorname{\mathrm{Gal}}(\overline{K}/K) \longrightarrow \left(\mathcal{O}/\ell\mathcal{O}\right)^{\times} \end{align*}$$
$$\begin{align*}\rho_{E, \ell} : \operatorname{\mathrm{Gal}}(\overline{K}/K) \longrightarrow \left(\mathcal{O}/\ell\mathcal{O}\right)^{\times} \end{align*}$$
 $\ell $
.
$\ell $
.
Invoking the proof of [Reference Zywina62, Proposition 2.7], we see that
![]() $m_E$
is only supported by
$m_E$
is only supported by
![]() $2$
and
$2$
and
![]() $3$
. Further,
$3$
. Further,
Therefore, for k coprime to
![]() $6$
, by (63),
$6$
, by (63),
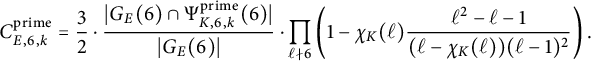 $$ \begin{align*} \begin{split} C_{E,6,k}^{\operatorname{\mathrm{prime}}} = \frac{3}{2} \cdot \frac{|G_E(6)\cap \Psi^{\operatorname{\mathrm{prime}}}_{K, 6, k}(6)|}{|G_E(6)|} \cdot \prod_{\ell \nmid 6}\left(1-\chi_K(\ell)\frac{\ell^2-\ell-1}{(\ell-\chi_K(\ell))(\ell-1)^2}\right). \end{split} \end{align*} $$
$$ \begin{align*} \begin{split} C_{E,6,k}^{\operatorname{\mathrm{prime}}} = \frac{3}{2} \cdot \frac{|G_E(6)\cap \Psi^{\operatorname{\mathrm{prime}}}_{K, 6, k}(6)|}{|G_E(6)|} \cdot \prod_{\ell \nmid 6}\left(1-\chi_K(\ell)\frac{\ell^2-\ell-1}{(\ell-\chi_K(\ell))(\ell-1)^2}\right). \end{split} \end{align*} $$
By adapting Suther land’s Galrep code [Reference Sutherland56], we compute
![]() $G_E(6)$
in Magma and find that
$G_E(6)$
in Magma and find that
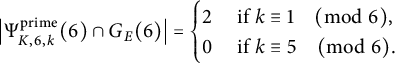 $$\begin{align*}\left|\Psi^{\operatorname{\mathrm{prime}}}_{K,6,k}(6)\cap G_E(6) \right| =\begin{cases} 2 & \text{ if }k \equiv 1 \quad\pmod{6}, \\ 0 & \text{ if } k \equiv 5 \quad\pmod{6}. \end{cases} \end{align*}$$
$$\begin{align*}\left|\Psi^{\operatorname{\mathrm{prime}}}_{K,6,k}(6)\cap G_E(6) \right| =\begin{cases} 2 & \text{ if }k \equiv 1 \quad\pmod{6}, \\ 0 & \text{ if } k \equiv 5 \quad\pmod{6}. \end{cases} \end{align*}$$
Thus, we conclude that
where
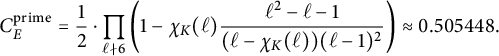 $$\begin{align*}C_{E}^{\operatorname{\mathrm{prime}}} = \frac{1}{2} \cdot \prod_{\ell \nmid 6}\left(1-\chi_K(\ell)\frac{\ell^2-\ell-1}{(\ell-\chi_K(\ell))(\ell-1)^2}\right) \approx 0.505448. \end{align*}$$
$$\begin{align*}C_{E}^{\operatorname{\mathrm{prime}}} = \frac{1}{2} \cdot \prod_{\ell \nmid 6}\left(1-\chi_K(\ell)\frac{\ell^2-\ell-1}{(\ell-\chi_K(\ell))(\ell-1)^2}\right) \approx 0.505448. \end{align*}$$
In fact, we can verify that
![]() $C^{\operatorname {\mathrm {prime}}}_{E,6,5} = 0$
using Deuring’s criterion. If p is a rational prime such that
$C^{\operatorname {\mathrm {prime}}}_{E,6,5} = 0$
using Deuring’s criterion. If p is a rational prime such that
![]() $p \equiv 5 \ \pmod 6$
, then p is inert in the CM field
$p \equiv 5 \ \pmod 6$
, then p is inert in the CM field
![]() $\mathbb {Q}(\sqrt {-3})$
. By Deuring’s criterion, p is supersingular, and hence
$\mathbb {Q}(\sqrt {-3})$
. By Deuring’s criterion, p is supersingular, and hence
![]() $|\widetilde {E}_p(\mathbb {F}_p)| = p+1$
. Since p is an odd prime, we see that p cannot be a prime of Koblitz reduction for E.
$|\widetilde {E}_p(\mathbb {F}_p)| = p+1$
. Since p is an odd prime, we see that p cannot be a prime of Koblitz reduction for E.
Acknowledgements
This article emerged from some initial conversations at the 2023 LuCaNT (LMFDB, Computation, and Number Theory) conference held at ICERM (Institute for Computational and Experimental Research in Mathematics). We are grateful to the conference organizers and the organizations that provided funding. An earlier version of this manuscript appears in the first author’s doctoral thesis. We are thankful for the doctoral committee members for their helpful comments. The third author, who conducted most of the work at the Max Planck Institute for Mathematics, is grateful for its funding and stimulating atmosphere of research.