Hostname: page-component-7dd5485656-bt4hw Total loading time: 0 Render date: 2025-10-29T04:06:29.579Z Has data issue: false hasContentIssue false
  • English
  • Français

Optimal Polynomial Recurrence

Published online by Cambridge University Press:  20 November 2018

Neil Lyall  and
Ákos Magyar
Neil Lyall
Affiliation:
Department of Mathematics, The University of Georgia, Athens, GA 30602, USA, e-mail: lyall@math.uga.edu
Ákos Magyar
Affiliation:
Department of Mathematics, University of British Columbia, Vancouver, BC V6T 1Z2, e-mail: magyar@math.ubc.ca
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 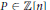$P\in \mathbb{Z}\left[ n \right]$ with 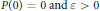$P(0)\,=\,0\,\text{and}\,\varepsilon \,>\,0$ . We show, using Fourier analytic techniques, that if 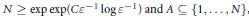$N\ge \exp \exp \left( C{{\varepsilon }^{-1}}\log {{\varepsilon }^{-1}} \right)\,\text{and}\,A\,\subseteq \,\left\{ 1,\,.\,.\,.\,,\,N \right\}$ then there must exist 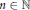$n\in \mathbb{N}$ such that

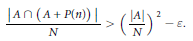$$\frac{\left| A\cap \left( A+P\left( n \right) \right) \right|}{N}>{{\left( \frac{\left| A \right|}{N} \right)}^{2}}-\,\varepsilon $$
.

In addition to this we show, using the same Fourier analytic methods, that if 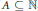$A\subseteq \mathbb{N}$ , then the setof $\varepsilon $ -optimal return times

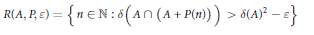$$R\left( A,P,\varepsilon\right)=\left\{ n\in \mathbb{N}:\delta \left( A\cap \left. \left( A+P\left( n \right) \right) \right)> \right.\delta {{\left( A \right)}^{2}}-\varepsilon\right\}$$

is syndetic for every 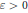$\varepsilon >0$ . Moreover, we show that 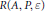$R\left( A,\,P,\,\varepsilon\right)$ is dense in every sufficiently long interval, in particular we show that there exists an 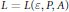$L=L\left( \varepsilon ,P,A \right)$ such that

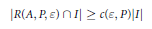$$\left| R\left( A,P,\varepsilon\right)\cap I \right|\ge c\left( \varepsilon ,P \right)\left| I \right|$$

for all intervals 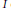$I$ of natural numbers with 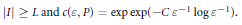$\left| I \right|\,\ge \,L\,\text{and}\,c\left( \varepsilon ,\,P \right)\,=\,\exp \exp \,\left( -C\,{{\varepsilon }^{-1}}\,\log {{\varepsilon }^{-1}} \right).$

Keywords

11B30Sarkozysyndeticpolynomial return times

Information

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 65 , Issue 1 , 01 February 2013 , pp. 171 - 194
Copyright
Copyright © Canadian Mathematical Society 2013

References

[1] Bergelson, V., The multifarious Poincaré recurrence theorem. In: Descriptive set theory and dynamical systems (Marseille–Luminy, 1996), London Math. Soc. Lecture Note Ser. 277, Cambridge Univ. Press, Cambridge, 2000, 31–57.Google Scholar
[2] Bergelson, V., Combinatorial and Diophantine applications of ergodic theory. Handbook of dynamical systems, Vol. 1B, Elsevier B.V., Amsterdam, 2006, 745–869.Google Scholar
[3]Bourgain, J., A Szemer´edi type theorem for sets of positive density in Rk, Israel J. Math. 54(1986), 307–316. http://dx.doi.org/10.1007/BF02764959 Google Scholar
[4]Frantzikinakis, N. and Kra, B., Ergodic averages for independent polynomials and applications. J. London Math. Soc. (2) 74(2006), 131–142. http://dx.doi.org/10.1112/S0024610706023374 Google Scholar
[5]Frantzikinakis, N. and McCutcheon, R., Ergodic Theory: Recurrence. In: Encyclopedia of Complexity and System Science, Part 5, Springer, 2009, 3083–3095.Google Scholar
[6]Furstenberg, H., Ergodic behavior of diagonal measures and a theorem of Szemer´edi on arithmetic progressions. J. Analyse Math. 71(1977), 204–256. http://dx.doi.org/10.1007/BF02813304 Google Scholar
[7] Green, B. and Tao, T., An arithmetic regularity lemma, associated counting lemma, and applications. In: An irregular mind: Szemeredi is 70, Bolyai Society Math. Stud. 21(2010).Google Scholar
[8] Khintchine, A. Y., Eine Verschärfung des Poincaréscen “Wiederkehrsatzes”. Compositio Math. 1(1934), 177–179.Google Scholar
[9]Kra, B., Ergodic methods in additive combinatorics. In: Additive combinatorics, CRM Proc. Lecture Notes 43, Amer. Math. Soc., Providence, RI, 2007, 103–144.Google Scholar
[10] Lyall, N. and Magyar, Á., Polynomial configurations in difference sets. J. Number Theory 129(2009), 439–450. http://dx.doi.org/10.1016/j.jnt.2008.05.003 Google Scholar
[11] Lyall, N., Polynomial configurations in difference sets (revised version). arxiv:arxiv.org/abs/0903.4504 http://dx.doi.org/10.1016/j.jnt.2008.05.003 Google Scholar
[12] Lyall, N., An optimal version of Sárközy's theorem. arxiv:arxiv.org/abs/1010.3451 Google Scholar
[13] Lyall, N., Simultaneous polynomial recurrence. Bull. London Math. Soc. 43(2011), 765–785 http://dx.doi.org/10.1112/blms/bdr011 Google Scholar
[14] Magyar, Á., On distance sets of large sets of integer points. Israel J. Math. 164(2008), 251–263. http://dx.doi.org/10.1007/s11856-008-0028-z Google Scholar
[15] McCutcheon, R., Elemental methods in ergodic Ramsey theory. Lecture Notes in Math. 1722, Springer-Verlag, Berlin, 1999.Google Scholar
[16]Poincaré, H., Les méthodes nouvelles de la mécanique céleste. I. Gauthiers-Villars, Paris 1892; II, 1893; III, 1899.Google Scholar