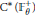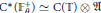Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Davidson, Kenneth R.
Power, Stephen C.
and
Yang, Dilian
2008.
Atomic representations of rank 2 graph algebras.
Journal of Functional Analysis,
Vol. 255,
Issue. 4,
p.
819.
PASK, DAVID
RAEBURN, IAIN
and
WEAVER, NATASHA A.
2010.
PERIODIC 2-GRAPHS ARISING FROM SUBSHIFTS.
Bulletin of the Australian Mathematical Society,
Vol. 82,
Issue. 1,
p.
120.
Power, Stephen C.
and
Solel, Baruch
2011.
Operator algebras associated with unitary commutation relations.
Journal of Functional Analysis,
Vol. 260,
Issue. 6,
p.
1583.
Fuller, Adam Hanley
2011.
Finitely correlated representations of product systems of C⁎-correspondences over Nk.
Journal of Functional Analysis,
Vol. 260,
Issue. 2,
p.
574.
Evans, D. Gwion
and
Sims, Aidan
2012.
When is the Cuntz–Krieger algebra of a higher-rank graph approximately finite-dimensional?.
Journal of Functional Analysis,
Vol. 263,
Issue. 1,
p.
183.
Kumjian, Alex
Pask, David
and
Sims, Aidan
2012.
Homology for higher-rank graphs and twisted C⁎-algebras.
Journal of Functional Analysis,
Vol. 263,
Issue. 6,
p.
1539.
Kumjian, Alex
Pask, David
and
Sims, Aidan
2013.
On theK-theory of twisted higher-rank-graphC∗-algebras.
Journal of Mathematical Analysis and Applications,
Vol. 401,
Issue. 1,
p.
104.
Brownlowe, Nathan
and
Raeburn, Iain
2013.
Two families of Exel–Larsen crossed products.
Journal of Mathematical Analysis and Applications,
Vol. 398,
Issue. 1,
p.
68.
Hazlewood, Robert
Raeburn, Iain
Sims, Aidan
and
Webster, Samuel B. G.
2013.
Remarks on some fundamental results about higher-rank graphs and their C*-algebras.
Proceedings of the Edinburgh Mathematical Society,
Vol. 56,
Issue. 2,
p.
575.
Maloney, Ben
Pask, David
and
Raeburn, Iain
2014.
Skew-products of higher-rank graphs and crossed products by semigroups.
Semigroup Forum,
Vol. 88,
Issue. 1,
p.
162.
Kang, Sooran
and
Pask, David
2014.
Aperiodicity and primitive ideals of row-finite k-graphs.
International Journal of Mathematics,
Vol. 25,
Issue. 03,
p.
1450022.
Brownlowe, Nathan
Ramagge, Jacqui
Robertson, David
and
Whittaker, Michael F.
2014.
Zappa–Szép products of semigroups and theirC⁎-algebras.
Journal of Functional Analysis,
Vol. 266,
Issue. 6,
p.
3937.
an Huef, Astrid
Laca, Marcelo
Raeburn, Iain
and
Sims, Aidan
2014.
KMS states onC⁎-algebras associated to higher-rank graphs.
Journal of Functional Analysis,
Vol. 266,
Issue. 1,
p.
265.
Carlsen, Toke Meier
Kang, Sooran
Shotwell, Jacob
and
Sims, Aidan
2014.
The primitive ideals of the Cuntz–Krieger algebra of a row-finite higher-rank graph with no sources.
Journal of Functional Analysis,
Vol. 266,
Issue. 4,
p.
2570.
Yang, Dilian
2015.
Cycline subalgebras of 𝑘-graph C*-algebras.
Proceedings of the American Mathematical Society,
Vol. 144,
Issue. 7,
p.
2959.
Brown, Jonathan H.
and
an Huef, Astrid
2015.
The Socle and Semisimplicity of a Kumjian–Pask Algebra.
Communications in Algebra,
Vol. 43,
Issue. 7,
p.
2703.
an Huef, Astrid
Laca, Marcelo
Raeburn, Iain
and
Sims, Aidan
2015.
KMS states on the C⁎-algebra of a higher-rank graph and periodicity in the path space.
Journal of Functional Analysis,
Vol. 268,
Issue. 7,
p.
1840.
YANG, DILIAN
2015.
PERIODIC -GRAPH ALGEBRAS REVISITED.
Journal of the Australian Mathematical Society,
Vol. 99,
Issue. 2,
p.
267.
Laca, Marcelo
Larsen, Nadia S.
Neshveyev, Sergey
Sims, Aidan
and
Webster, Samuel B. G.
2015.
Von Neumann algebras of strongly connected higher-rank graphs.
Mathematische Annalen,
Vol. 363,
Issue. 1-2,
p.
657.
an Huef, Astrid
Kang, Sooran
and
Raeburn, Iain
2015.
Spatial realisations of KMS states on the C⁎-algebras of higher-rank graphs.
Journal of Mathematical Analysis and Applications,
Vol. 427,
Issue. 2,
p.
977.