Hostname: page-component-7dd5485656-wxk4p Total loading time: 0 Render date: 2025-10-31T20:49:10.720Z Has data issue: false hasContentIssue false
  • English
  • Français

Polynomial Hulls of Sets Invariant Under an Action of the Special Unitary Group

Published online by Cambridge University Press:  20 November 2018

John T. Anderson
John T. Anderson*
Affiliation:
College of the Holy Cross, Worcester, Massachusetts
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

If K is a compact subset of C n , will denote the polynomial hull of K:

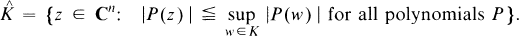
arises in the study of uniform algebras as the maximal ideal space of the algebra P(K) of uniform limits on K of polynomials (see [3]). The condition (K is polynomially convex) is a necessary one for uniform approximation on K of continuous functions by polynomials (P(K) = C(K)). If K is not polynomially convex, the question of existence of analytic structure in 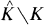is of particular interest. For n = 1, is the union of K and the bounded components of C\K. The determination of in dimensions greater than one is a more difficult problem. Among the special classes of compact sets K whose polynomial hulls have been determined are those invariant under certain group actions on C n .

Information

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 40 , Issue 5 , 01 October 1988 , pp. 1256 - 1271
Copyright
Copyright © Canadian Mathematical Society 1988

References

1. Adams, F., Lectures on Lie groups (W. A. Benjamin, N.Y., 1969).Google Scholar
2. Bjork, J.-E., Compact groups operating on Banach algebras, Math. Ann. 205 (1973), 281–297.Google Scholar
3. Browder, A., Introduction to function algebras (W. A. Benjamin, N.Y., 1969).Google Scholar
4. Browder, A., Cohomology of maximal ideal spaces, Bull. A.M.S. 67 (1961), 515–516.Google Scholar
5. Debiard, A. and Gaveau, B., Equations de Cauchy-Riemann sur SU(2) et leurs enveloppes d'holomorphie, Can. J. Math. 38 (1986), 1009–1024.Google Scholar
6. Gamelin, T., Hartogs series, Hartogs functions, and Jensen measures, in Spaces of analyticfunctions, Kristiansand, Norway (1975), Lecture Notes in Mathematics 512 (Springer-Verlag, N.Y., 1976).Google Scholar
7. Helgason, S., Differential geometry and symmetric spaces (Academic Press, N.Y., 1962).Google Scholar
8. Helms, L. L., Introduction to potential theory (John Wiley & Sons, N.Y., 1969).Google Scholar
9. Hormander, L. and J. Wermer, Uniform approximation on compact subsets in C n , Math. Scand. 23 (1968), 5–21.Google Scholar
10. Hua, L. K., On the theory ofautomorphic functions of a matrix variable I, Geometrical basis, Amer. J. Math. 66 (1944), 470–480.Google Scholar
11. Rudin, W., Function theory on the unit ball in C n (Springer-Verlag, N.Y., 1980).CrossRefGoogle Scholar
12. Wermer, J., Subharmonicity and hulls, Pac. J. Math. 38 (1975), 283–290.Google Scholar