Article contents
Predual of the Multiplier Algebra of Ap (G) and Amenability
Published online by Cambridge University Press: 20 November 2018
Abstract
For a locally compact group 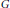 $G$ and
$G$ and 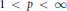 $1\,<\,p\,<\,\infty $ , let
$1\,<\,p\,<\,\infty $ , let 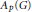 ${{A}_{p}}\left( G \right)$ be the Herz-Figà-Talamanca algebra and let
${{A}_{p}}\left( G \right)$ be the Herz-Figà-Talamanca algebra and let 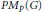 $P{{M}_{p}}\left( G \right)$ be its dual Banach space. For a Banach
$P{{M}_{p}}\left( G \right)$ be its dual Banach space. For a Banach 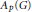 ${{A}_{p}}\left( G \right)$ -module
${{A}_{p}}\left( G \right)$ -module  $X$ of
$X$ of 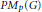 $P{{M}_{p}}\left( G \right)$ , we prove that the multiplier space
$P{{M}_{p}}\left( G \right)$ , we prove that the multiplier space 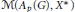 $\text{M}\left( {{A}_{p}}\left( G \right),{{X}^{*}} \right)$ is the dual Banach space of
$\text{M}\left( {{A}_{p}}\left( G \right),{{X}^{*}} \right)$ is the dual Banach space of 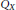 ${{Q}_{X}}$ , where
${{Q}_{X}}$ , where 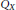 ${{Q}_{X}}$ is the norm closure of the linear span
${{Q}_{X}}$ is the norm closure of the linear span 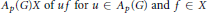 ${{A}_{p}}\left( G \right)X\,\text{of}\,u\,f\,\text{for}\,u\,\in \,{{A}_{p}}\left( G \right)\,\text{and}\,f\,\in \,X$ in the dual of
${{A}_{p}}\left( G \right)X\,\text{of}\,u\,f\,\text{for}\,u\,\in \,{{A}_{p}}\left( G \right)\,\text{and}\,f\,\in \,X$ in the dual of 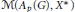 $\text{M}\left( {{A}_{p}}\left( G \right),{{X}^{*}} \right)$ . If
$\text{M}\left( {{A}_{p}}\left( G \right),{{X}^{*}} \right)$ . If 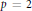 $p\,=\,2$ and
$p\,=\,2$ and 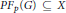 $P{{F}_{p}}\left( G \right)\subseteq X$ , then
$P{{F}_{p}}\left( G \right)\subseteq X$ , then 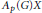 ${{A}_{p}}\left( G \right)X$ is closed in
${{A}_{p}}\left( G \right)X$ is closed in  $X$ if and only if
$X$ if and only if 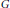 $G$ is amenable. In particular, we prove that the multiplier algebra
$G$ is amenable. In particular, we prove that the multiplier algebra 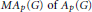 $M{{A}_{p}}\left( G \right)\,\text{of}\,{{A}_{p}}\left( G \right)$ is the dual of
$M{{A}_{p}}\left( G \right)\,\text{of}\,{{A}_{p}}\left( G \right)$ is the dual of 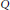 $Q$ , where
$Q$ , where 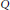 $Q$ is the completion of
$Q$ is the completion of 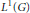 ${{L}^{1}}\left( G \right)$ in the
${{L}^{1}}\left( G \right)$ in the 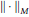 $||\cdot |{{|}_{M}}$ -norm.
$||\cdot |{{|}_{M}}$ -norm. 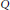 $Q$ is characterized by the following:
$Q$ is characterized by the following: 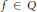 $f\,\in \,Q$ if an only if there are
$f\,\in \,Q$ if an only if there are 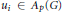 ${{u}_{i}}\,\in \,{{A}_{p}}\left( G \right)$ and
${{u}_{i}}\,\in \,{{A}_{p}}\left( G \right)$ and 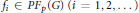 ${{f}_{i}}\in P{{F}_{p}}\left( G \right)\left( i=1,2,... \right)$ with
${{f}_{i}}\in P{{F}_{p}}\left( G \right)\left( i=1,2,... \right)$ with 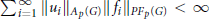 $\sum\nolimits_{i=1}^{\infty }{||}\,{{u}_{i}}\,|{{|}_{{{A}_{p}}\left( G \right)}}||fi|{{|}_{P{{F}_{p}}\left( G \right)}}\,<\,\infty $ such that
$\sum\nolimits_{i=1}^{\infty }{||}\,{{u}_{i}}\,|{{|}_{{{A}_{p}}\left( G \right)}}||fi|{{|}_{P{{F}_{p}}\left( G \right)}}\,<\,\infty $ such that 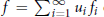 $f=\sum{_{i=1}^{\infty }\,{{u}_{i}}{{f}_{i}}}$ on
$f=\sum{_{i=1}^{\infty }\,{{u}_{i}}{{f}_{i}}}$ on 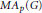 $M{{A}_{p}}\left( G \right)$ . It is also proved that if
$M{{A}_{p}}\left( G \right)$ . It is also proved that if 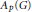 ${{A}_{p}}\left( G \right)$ is dense in
${{A}_{p}}\left( G \right)$ is dense in 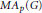 $M{{A}_{p}}\left( G \right)$ in the associated
$M{{A}_{p}}\left( G \right)$ in the associated 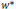 ${{w}^{*}}$ -topology, then the multiplier norm and
${{w}^{*}}$ -topology, then the multiplier norm and 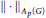 $||\cdot |{{|}_{{{A}_{p}}\left( G \right)}}$ -norm are equivalent on
$||\cdot |{{|}_{{{A}_{p}}\left( G \right)}}$ -norm are equivalent on 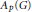 ${{A}_{p}}\left( G \right))$ if and only if
${{A}_{p}}\left( G \right))$ if and only if 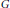 $G$ is amenable.
$G$ is amenable.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 2004
References
- 6
- Cited by

