No CrossRef data available.
Published online by Cambridge University Press: 20 November 2018
Le diagramme d’Eisenbud et Neumann d’un germe est un arbre qui représente ce germe et permet d’en calculer les invariants. On donne une démonstration algébrique d’un résultat caractérisant l’ensemble des quotients jacobiens d’un germe d’application 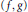 $(f,\,g)$ à partir du diagramme d’Eisenbud et Neumann de
$(f,\,g)$ à partir du diagramme d’Eisenbud et Neumann de 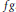 $fg$ .
$fg$ .
The Eisenbud and Neumann diagram of a plane curve germ is a tree that represents this germ and allows computation of its invariants. We algebraically show a result that gives a caracterization of the set of jacobian quotients of an application germ 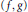 $(f,\,g)$ for the datum of the Eisenbud et Neumann diagram of
$(f,\,g)$ for the datum of the Eisenbud et Neumann diagram of 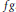 $fg$ .
$fg$ .