Article contents
Quotients of A 2 * T 2
Published online by Cambridge University Press: 20 November 2018
Abstract
We study unitary quotients of the free product unitary pivotal category 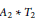 ${{A}_{2}}\,*\,{{T}_{2}}$ . We show that such quotients are parametrized by an integer
${{A}_{2}}\,*\,{{T}_{2}}$ . We show that such quotients are parametrized by an integer 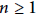 $n\,\ge \,1$ and an
$n\,\ge \,1$ and an 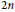 $2n$ –th root of unity
$2n$ –th root of unity 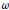 $\omega $ . We show that for
$\omega $ . We show that for 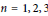 $n\,=\,1,\,2,\,3$ , there is exactly one quotient and
$n\,=\,1,\,2,\,3$ , there is exactly one quotient and 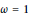 $\omega \,=\,1$ . For
$\omega \,=\,1$ . For 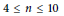 $4\,\le \,n\,\le \,10$ , we show that there are no such quotients. Our methods also apply to quotients of
$4\,\le \,n\,\le \,10$ , we show that there are no such quotients. Our methods also apply to quotients of 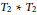 ${{T}_{2}}\,*\,{{T}_{2}}$ , where we have a similar result.
${{T}_{2}}\,*\,{{T}_{2}}$ , where we have a similar result.
The essence of our method is a consistency check on jellyfish relations. While we only treat the specific cases of 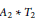 ${{A}_{2}}\,*\,{{T}_{2}}$ and
${{A}_{2}}\,*\,{{T}_{2}}$ and 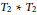 ${{T}_{2}}\,*\,{{T}_{2}}$ , we anticipate that our technique can be extended to a general method for proving the nonexistence of planar algebras with a specified principal graph.
${{T}_{2}}\,*\,{{T}_{2}}$ , we anticipate that our technique can be extended to a general method for proving the nonexistence of planar algebras with a specified principal graph.
During the preparation of this manuscript, we learnt of Liu's independent result on composites of 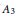 ${{A}_{3}}$ and
${{A}_{3}}$ and 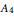 ${{A}_{4}}$ subfactor planar algebras (arxiv:1308.5691). In 1994, Bisch–Haagerup showed that the principal graph of a composite of
${{A}_{4}}$ subfactor planar algebras (arxiv:1308.5691). In 1994, Bisch–Haagerup showed that the principal graph of a composite of 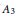 ${{A}_{3}}$ and
${{A}_{3}}$ and 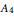 ${{A}_{4}}$ must fit into a certain family, and Liu has classified all such subfactor planar algebras. We explain the connection between the quotient categories and the corresponding composite subfactor planar algebras. As a corollary of Liu's result, there are no such quotient categories for
${{A}_{4}}$ must fit into a certain family, and Liu has classified all such subfactor planar algebras. We explain the connection between the quotient categories and the corresponding composite subfactor planar algebras. As a corollary of Liu's result, there are no such quotient categories for 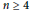 $n\,\ge \,4$ .
$n\,\ge \,4$ .
This is an abridged version of arxiv:1308.5723.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 2016
References
- 3
- Cited by

