No CrossRef data available.
Article contents
Reducible Riemannian manifolds with conformal product structures
Published online by Cambridge University Press: 24 November 2025
Abstract
We study conformal product structures on compact reducible Riemannian manifolds, and show that under a suitable technical assumption, the underlying Riemannian manifolds are either conformally flat or local triple products, i.e., locally isometric to Riemannian manifolds of the form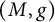 
$(M,g)$ with 
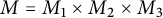$M=M_1\times M_2\times M_3$ and 
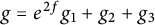$g=e^{2f}g_1+g_2+g_3$, where 
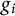$g_i$ is a Riemannian metric on 
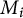$M_i$, for 
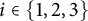$i\in \{1,2,3\}$, and 
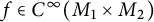$f\in C^\infty (M_1\times M_2)$.
Information
- Type
- Article
- Information
- Copyright
- © The Author(s), 2025. Published by Cambridge University Press on behalf of Canadian Mathematical Society
Footnotes
This work was partly supported by the PNRR-III-C9-2023-I8 grant CF 149/31.07.2023 Conformal Aspects of Geometry and Dynamics.
References
Belgun, F., Flamencourt, B., and Moroianu, A.,
Weyl structures with special holonomy on compact conformal manifolds
. Doc. Math. (2025). https://doi.org/10.4171/DM/1033
Google Scholar
Belgun, F. and Moroianu, A.,
Weyl-parallel forms, conformal products and Einstein-Weyl manifolds
. Asian J. Math. 15(2011), 499–520.Google Scholar
Belgun, F. and Moroianu, A.,
On the irreducibility of locally metric connections
. J. Reine Angew. Math. 714(2016), 123–150.Google Scholar
Calderbank, D. M. J., Selfdual Einstein metrics and conformal submersions. Preprint, 2000. arXiv:math/0001041v1.Google Scholar
Flamencourt, B.,
Locally conformally product structures
. Int. J. Math. 35(2024), no. 5, 2450013.Google Scholar
Flamencourt, B. and Zeghib, A., On foliations admitting a transverse similarity structure. Preprint, 2025. arXiv:2501.04814.Google Scholar
Fried, D.,
Closed similarity manifolds
. Comment. Math. Helv. 55(1980), no. 4, 576–582.Google Scholar
Gauduchon, P.,
Structures de Weyl-Einstein, espaces de twisteurs et variétés de type
${S}^1\times {S}^3$
. J. Reine Angew. Math. 469(1995), 1–50
Google Scholar
${S}^1\times {S}^3$
. J. Reine Angew. Math. 469(1995), 1–50
Google ScholarKourganoff, M.,
Similarity structures and de Rham decomposition
. Math. Ann. 373(2019), 1075–1101.Google Scholar
Kühnel, W. and Rademacher, H.-B.,
Conformal vector fields on pseudo-Riemannian spaces
. Differ. Geom. Appl. 7(1997), 237–250.Google Scholar
Kühnel, W. and Rademacher, H.-B.,
Einstein spaces with a conformal group
. Res. Math. 56(2009), 421–444.Google Scholar
Kühnel, W. and Rademacher, H.-B.,
Conformally Einstein product spaces
. Differ. Geom. Appl. 49(2016), 65–96.Google Scholar
Matveev, V. and Nikolayevsky, Y.,
A counterexample to Belgun-Moroianu conjecture
. C. R. Math. Acad. Sci. Paris 353(2015), 455–457.Google Scholar
Matveev, V. and Nikolayevsky, Y.,
Locally conformally Berwald manifolds and compact quotients of reducible manifolds by homotheties
. Ann. Inst. Fourier (Grenoble) 67(2017), no. 2, 843–862.Google Scholar
Merkulov, S. and Schwachhöfer, L.,
Classification of irreducible holonomies of torsion-free affine connections
. Ann. Math. 150(1999), no. 1, 77–149.Google Scholar
Moroianu, A.,
Conformally related Riemannian metrics with non-generic holonomy
. J. Reine Angew. Math. 755(2019), 279–292.Google Scholar
Moroianu, A. and Pilca, M.,
Einstein metrics on conformal products
. Ann. Glob. Anal. Geom. 65(2024), 20.Google Scholar
Moroianu, A. and Pilca, M.,
Conformal product structures on compact Kähler manifolds
. Adv. Math. 467(2025), Article no. 110181.Google Scholar
Moroianu, A. and Pilca, M., Conformal product structures on compact Einstein manifolds. Preprint, 2025. arXiv2504.07886.Google Scholar