No CrossRef data available.
Article contents
Resolution D'Equations Associees a un Systeme de Tchebycheff
Published online by Cambridge University Press: 20 November 2018
Extract
Soit {f 1(x),f 2(x), …,fm (x)} un système de Tchebycheff de dimension m, c'est-à-dire les fonctions fj (x) sont des fonctions réelles continues définies sur un intervalle ouvert (a, b) et toute fonction de la forme 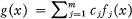 admet au plus m — 1 racines dans (a, b) lorsqu'au moins un des coefficients Cj diffère de 0. Notre point de départ est un théorème dû à Krein [3]. On se limite au cas où la dimension m est paire, m = 2n. Ce théorème dit que la totalité Ω des points
admet au plus m — 1 racines dans (a, b) lorsqu'au moins un des coefficients Cj diffère de 0. Notre point de départ est un théorème dû à Krein [3]. On se limite au cas où la dimension m est paire, m = 2n. Ce théorème dit que la totalité Ω des points 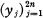 de R 2n qui se représentent ainsi
de R 2n qui se représentent ainsi 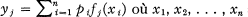 sont n points distincts de (a, b) et où pi > 0, 1 ≦ i≦n, forme effectivement un ouvert convexe de R 2n . Les systèmes d'équations que nous voulons traiter sont justement les équations:
sont n points distincts de (a, b) et où pi > 0, 1 ≦ i≦n, forme effectivement un ouvert convexe de R 2n . Les systèmes d'équations que nous voulons traiter sont justement les équations:
I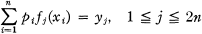
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 1982

