Hostname: page-component-76fb5796d-25wd4 Total loading time: 0 Render date: 2024-04-27T12:42:28.575Z Has data issue: false hasContentIssue false
  • English
  • Français

Riesz-type criteria for L-functions in the Selberg class

Part of: Zeta and $L$-functions: analytic theory

Published online by Cambridge University Press:  29 May 2023

Shivajee Gupta  and
Akshaa Vatwani Open the ORCID record for Akshaa Vatwani [Opens in a new window]
Shivajee Gupta
Affiliation:
Discipline of Mathematics, Indian Institute of Technology Gandhinagar, Palaj, Gandhinagar, India e-mail: shivajee.o@iitgn.ac.in
Akshaa Vatwani*
Affiliation:
Discipline of Mathematics, Indian Institute of Technology Gandhinagar, Palaj, Gandhinagar, India e-mail: shivajee.o@iitgn.ac.in
*
e-mail: akshaa.vatwani@iitgn.ac.in
Get access Rights & Permissions [Opens in a new window]

Abstract

We formulate a generalization of Riesz-type criteria in the setting of L-functions belonging to the Selberg class. We obtain a criterion which is sufficient for the grand Riemann hypothesis (GRH) for L-functions satisfying axioms of the Selberg class without imposing the Ramanujan hypothesis on their coefficients. We also construct a subclass of the Selberg class and prove a necessary criterion for GRH for L-functions in this subclass. Identities of Ramanujan–Hardy–Littlewood type are also established in this setting, specific cases of which yield new transformation formulas involving special values of the Meijer G-function of the type 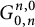${G^{n , 0}_{0 , n}}$.

Keywords

Selberg classgrand Riemann hypothesisRiesz-type criteriamodular relations

MSC classification

Primary: 11M06: $zeta (s)$ and $L(s, chi)$
Secondary: 11M26: Nonreal zeros of $zeta (s)$ and $L(s, chi)$; Riemann and other hypotheses 11M41: Other Dirichlet series and zeta functions 33C20: Generalized hypergeometric series, $_pF_q$
Type
Article
Information
Canadian Journal of Mathematics , First View , pp. 1 - 27
Check for updates
Copyright
© The Author(s), 2023. Published by Cambridge University Press on behalf of The Canadian Mathematical Society

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

The first author was supported by the Shyama Prasad Mukherjee fellowship CSIR SPM-06/1031(0281)/2018-EMR-I. The second author was supported by the MHRD SPARC project SPARC/2018-2019/P567/SL, the SERB-DST grant ECR/2018/001566, and the DST INSPIRE Faculty Award Program DST/INSPIRE/Faculty/Batch-13/2018.

References

Agarwal, A., Garg, M. and Maji, B., Riesz-type criteria for the Riemann Hypothesis. Proc. Amer. Math. Soc., 150 (2022), no. 12, 5151–5163.Google Scholar
Aistleitner, C. and Pańkowski, Ł., Large values of L-functions from the Selberg class . J. Math. Anal. Appl. 446(2017), 345–364.CrossRefGoogle Scholar
Banerjee, S. and Kumar, R., Equivalent criterion for the grand Riemann hypothesis associated to Maass cusp forms. Preprint, 2021. arXiv:2112.08143.Google Scholar
Berndt, B. C., Ramanujan’s notebooks, Part V, Springer-Verlag, New York, 1998.CrossRefGoogle Scholar
Conrey, J. B. and Ghosh, A., On the Selberg class of Dirichlet series: Small degrees . Duke Math. J. 72(1993), 673–693.CrossRefGoogle Scholar
Copson, E. T., Theory of functions of a complex variable, Oxford University Press, Oxford, 1935.Google Scholar
Dixit, A., Character analogues of Ramanujan-type integrals involving the Riemann $\varXi$ -function . Pacific J. Math. 255(2012), no. 2, 317–348.CrossRefGoogle Scholar
Dixit, A., Analogues of the general theta transformation formula . Proc. Roy. Soc. Edinburgh Sect. A 143(2013), 371–399.CrossRefGoogle Scholar
Dixit, A., Gupta, S., and Vatwani, A., A modular relation involving non-trivial zeros of the Dedekind zeta function, and the generalized Riemann hypothesis . J. Math. Anal. Appl. 515(2022), 126435.CrossRefGoogle Scholar
Dixit, A. and Murty, V. K., The Lindelöf class of L-functions II . Int. J. Number Theory 15(2019), no. 10, 2201–2221.CrossRefGoogle Scholar
Dixit, A. and Murty, V. K., The Lindelöf class of $L$ -functions II . Int. J. Number Theory 15(2019), no. 10, 2201–2221.CrossRefGoogle Scholar
Dixit, A., Roy, A., and Zaharescu, A., Ramanujan–Hardy–Littlewood–Riesz phenomena for Hecke forms . J. Math. Anal. Appl. 426(2015), 594–611.CrossRefGoogle Scholar
Dixit, A., Roy, A., and Zaharescu, A., Riesz-type criteria and theta transformation analogues . J. Number Theory 160(2016), 385–408.CrossRefGoogle Scholar
Hardy, G. H. and Littlewood, J. E., Contributions to the theory of the Riemann zeta-function and the theory of the distribution of primes . Acta Math. 41(1916), 119–196.CrossRefGoogle Scholar
Iwaniec, H. and Kowalski, E., Analytic Number Theory, Colloquium Publications, 53, American Mathematical Society, Providence, RI, 2004.Google Scholar
Kühn, P., Robles, N., and Roy, A., On a class of functions that satisfies explicit formulae involving the Möbius function . Ramanujan J. 38(2015), 383–422.CrossRefGoogle Scholar
Kumar Murty, V., The Lindelöf class of $L$ -functions. In: The conference on L-functions, World Sci. Publ., Hackensack, NJ, 2007, pp. 165–174.Google Scholar
Luke, Y. L., The special functions and their approximations, vol. 1, Mathematics in Science and Engineering, Vol. 53 Academic Press, New York-London, 1969.Google Scholar
McLachlan, N. W., Complex variable theory and transform calculus, Cambridge University Press, Cambridge, 1963.Google Scholar
Mukhopadhyay, A. and Srinivas, K., A zero density estimate for the Selberg class . Int. J. Number Theory 3(2007), no. 2, 263–273.CrossRefGoogle Scholar
Perelli, A., A survey of the Selberg class of $L$ -functions, part I . Milan J. Math. 73(2004), 1–28.Google Scholar
Ramanujan, S., Notebooks , vols. 1, 2, Tata Institute of Fundamental Research, Bombay, 1957; reprint 2012.Google Scholar
Riesz, M., Sur l’hypothèse de Riemann . Acta Math. 40(1916), 185–190.CrossRefGoogle Scholar
Roy, A., Zaharescu, A., and Zaki, M., Some identities involving convolutions of Dirichlet characters and the Möbius function . Proc. Indian Acad. Sci. Math. Sci. 126(2016), no. 1, 21–33.CrossRefGoogle Scholar
Titchmarsh, E. C., The theory of the Riemann zeta-function, 2nd ed., Clarendon Press, Oxford, 1986.Google Scholar
Watson, G. N., A treatise on the theory of Bessel functions, 2nd ed., Cambridge University Press, London, 1944.Google Scholar