No CrossRef data available.
Published online by Cambridge University Press: 20 November 2018
In this paper we study ruled surfaces which appear as exceptional surface in a succession of blowing-ups. In particular we prove that the 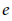 $e$-invariant of such a ruled exceptional surface
$e$-invariant of such a ruled exceptional surface 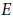 $E$ is strictly positive whenever its intersection with the other exceptional surfaces does not contain a fiber (of
$E$ is strictly positive whenever its intersection with the other exceptional surfaces does not contain a fiber (of 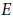 $E$). This fact immediately enables us to resolve an open problem concerning an intersection configuration on such a ruled exceptional surface consisting of three nonintersecting sections. In the second part of the paper we apply the non-vanishing of
$E$). This fact immediately enables us to resolve an open problem concerning an intersection configuration on such a ruled exceptional surface consisting of three nonintersecting sections. In the second part of the paper we apply the non-vanishing of 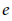 $e$ to the study of the poles of the well-known topological, Hodge and motivic zeta functions.
$e$ to the study of the poles of the well-known topological, Hodge and motivic zeta functions.