Hostname: page-component-8448b6f56d-sxzjt Total loading time: 0 Render date: 2024-04-24T04:10:10.668Z Has data issue: false hasContentIssue false
  • English
  • Français

Sector Analogue of the Gauss–Lucas Theorem

Part of: Geometric function theory

Published online by Cambridge University Press:  12 December 2019

Blagovest Sendov  and
Hristo Sendov
Blagovest Sendov
Affiliation:
Bulgarian Academy of Sciences, Institute of Information and Communication Technologies, Acad. G. Bonchev Str., bl. 25A, 1113 Sofia, Bulgaria
Hristo Sendov
Affiliation:
Department of Statistical and Actuarial Sciences, Western University, 1151 Richmond Str., London, ON, N6A 5B7 Canada Email: hssendov@stats.uwo.ca
Get access Rights & Permissions [Opens in a new window]

Abstract

The classical Gauss–Lucas theorem states that the critical points of a polynomial with complex coefficients are in the convex hull of its zeros. This fundamental theorem follows from the fact that if all the zeros of a polynomial are in a half plane, then the same is true for its critical points. The main result of this work replaces the half plane with a sector as follows.

We show that if the coefficients of a monic polynomial 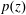$p(z)$ are in the sector {tei𝜓 : 𝜓∈ [0, 𝜙], t⩾0}, for some 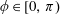$\unicode[STIX]{x1D719}\in [0,\unicode[STIX]{x1D70B})$, and the zeros are not in its interior, then the critical points of 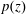$p(z)$ are also not in the interior of that sector.

In addition, we give a necessary condition for a polynomial to satisfy the premise of the main result.

Keywords

Gauss–Lucas theorempolynomialzeros and critical points of polynomialpolynomial with coefficients in a sectorinterlacing polynomialnon-convex

MSC classification

Primary: 30C10: Polynomials
Type
Article
Information
Canadian Journal of Mathematics , Volume 73 , Issue 2 , April 2021 , pp. 318 - 338
Check for updates
Copyright
© Canadian Mathematical Society 2019

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

The first author was partly supported by the Bulgarian National Science Fund under project FNI I 20/20 “Efficient Parallel Algorithms for Large-Scale Computational Problems”. The second author was partially supported by the Natural Sciences and Engineering Research Council (NSERC) of Canada.

†

Deceased.

References

Ćurgus, B. and Mascioni, V., A contraction of the Lucas polygon. Proc. Amer. Math. Soc. 132(2004), 2973–2981. https://doi.org/10.1090/S0002-9939-04-07231-4CrossRefGoogle Scholar
Díaz, D. B. and Shaffer, D. B., A generalization, to higher dimensions, of a theorem of Lucas concerning the zeros of the derivative of a polynomial of one complex variable. Applicable Anal. 6(1976/77), 109–117. https://doi.org/10.1080/00036817708839144CrossRefGoogle Scholar
Dimitrov, D. K., A refinement of the Gauss–Lucas theorem. Proc. Amer. Math. Soc. 126(1998), 2065–2070. https://doi.org/10.1090/S0002-9939-98-04381-0CrossRefGoogle Scholar
Goodman, A. W., Remarks on the Gauss–Lucas theorem in higher dimensional space. Proc. Amer. Math. Soc. 55(1976), 97–102.CrossRefGoogle Scholar
Malamud, S. M., Inverse spectral problem for normal matrices and the Gauss–Lucas theorem. Trans. Amer. Math. Soc. 357(2004), 4043–4064. https://doi.org/10.1090/S0002-9947-04-03649-9CrossRefGoogle Scholar
Pereira, R., Differentiators and the geometry of polynomials. J. Math. Anal. Appl. 285(2003), 336–348. https://doi.org/10.1016/S0022-247X(03)00465-7CrossRefGoogle Scholar
Rahman, Q. I. and Schmeisser, G., Analytic theory of polynomials. London Mathematical Society Monographs. New Series, 26, Oxford University Press, Oxford, 2002.Google Scholar
Rüdinger, A., Strengthening the Gauss–Lucas theorem for polynomials with zeros in the interior of the convex hull. arxiv:1405.0689v1Google Scholar
Totik, V., The Gauss–Lucas theorem in an asymptotic sense. Bull. London Math. Soc. 48(2016), 848–854. https://doi.org/10.1112/blms/bdw047CrossRefGoogle Scholar
Sendov, B. and Sendov, H. S., On the zeros and critical points of polynomials with non-negative coefficients: a non-convex analogue of the Gauss–Lucas theorem. Constr. Approx. 46(2017), 305–317. https://doi.org/10.1007/s00365-017-9374-6CrossRefGoogle Scholar
Specht, W., Eine Bemerkung zum Satze von Gauß-Lucas. Jber. Deutsch. Math.-Verein. 62(1959), 85–92.Google Scholar