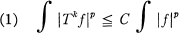A Simple Proof of the Maximal Ergodic Theorem

Alberto De La Torre

doi:10.4153/CJM-1976-106-8

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let X be a σ-finite measure space and let Tk, k any integer, be a group of positive linear transformations in Lp(X) such that

with C independent of / and k. From now on / will be a positive function in Lp(X) and we will use the following notation:

References

1. Akcoglu, M. A., A pointwise ergodic theorem inLp-spaces, Can. J. Math. 27 (1975), 1075–1082.Google Scholar

2. Calderon, A. P., Ergodic theory and translation invariant operators, Proc. Nat. Acad. Sci. 59 (1968), 349–353.Google Scholar

3. Coifman, R. R. and Weiss, G., Operators associated with representations of amendable groups, singular integrals induced by ergodic flows, the rotation method and multipliers, Studia Math. 47 (1973), 285–303.Google Scholar

4. Ionescu-Tulcea, A., Ergodic properties of isometries in Lp-spaces, Bull. Amer. Math. Soc. 70 (1964), 366–371.Google Scholar

5. Stein, E. M., Topics in harmonic analysis, Annals of Mathematics Studies 63.Google Scholar

6. Wiener, N., The ergodic theorem, Duke Math. J. 5 (1939), 1–18.Google Scholar

Crossref Citations

This article has been cited by the following publications. This list is generated based on data provided by Crossref.

Duncan, Richard 1977. Some Pointwise Convergence Results in Lp(μ), 1 < p < ∞. Canadian Mathematical Bulletin, Vol. 20, Issue. 3, p. 277.

1985. Ergodic Theorems. p. 321.

Assani, I. 1986. On the punctual and local ergodic theorem for nonpositive power bounded operators in 𝐿^{𝑝}_{𝐶}[0,1],1<𝑝<+∞. Proceedings of the American Mathematical Society, Vol. 96, Issue. 2, p. 306.

Sato, R. 1986. An individual ergodic theorem for superadditive processes. Acta Mathematica Hungarica, Vol. 47, Issue. 1-2, p. 153.

Zaharopol, Radu 1989. On the maximal ergodic theorem. Journal of Mathematical Analysis and Applications, Vol. 142, Issue. 1, p. 1.

Lin, Michael and Wittmann, Rainer 1994. Ergodic sequences of averages of group representations. Ergodic Theory and Dynamical Systems, Vol. 14, Issue. 1, p. 181.

Jajte, Ryszard 2004. Individual ergodic theorem for unitary maps of random matrices. Proceedings of the American Mathematical Society, Vol. 132, Issue. 8, p. 2475.

Яйте, Ричард and Jajte, Ryszard 2006. Индивидуальная эргодическая теорема для сжатий в пространствах $\mathbb{L}_p(\mathcal{H})$. Функциональный анализ и его приложения, Vol. 40, Issue. 2, p. 90.

Jajte, R. 2006. A pointwise ergodic theorem for contractions in $$\mathbb{L}_p $$ (ℋ)-spaces. Functional Analysis and Its Applications, Vol. 40, Issue. 2, p. 159.

Cabral, Adrián and Martín-Reyes, Francisco J. 2018. Sharp bound for the ergodic maximal operator associated to Cesàro bounded operators. Journal of Mathematical Analysis and Applications, Vol. 462, Issue. 1, p. 648.

Cohen, Guy 2018. Doubly power-bounded operators on L, 2 ≠ p > 1. Journal of Mathematical Analysis and Applications, Vol. 466, Issue. 2, p. 1327.

Martín-Reyes, Francisco J. and de la Rosa, Elena 2022. Ergodic theorems for Cesàro bounded operators in L1. Journal of Mathematical Analysis and Applications, Vol. 509, Issue. 2, p. 125973.

Hong, Guixiang Ray, Samya Kumar and Wang, Simeng 2023. Maximal ergodic inequalities for some positive operators on noncommutative Lp$L_p$‐spaces. Journal of the London Mathematical Society, Vol. 108, Issue. 1, p. 362.

Article contents

A Simple Proof of the Maximal Ergodic Theorem

Extract

References

Save article to Kindle

Save article to Dropbox

Save article to Google Drive

Reply to: Submit a response

Your details

You have entered the maximum number of contributors

Conflicting interests