Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Berg, Christian
and
Durán, Antonio J.
2008.
Iteration of the rational function z-1/z and a Hausdorff moment sequence.
Expositiones Mathematicae,
Vol. 26,
Issue. 4,
p.
375.
Berg, Christian
and
Petersen, Helle Bjerg
2013.
On an Iteration Leading to a q-Analogue of the Digamma Function.
Journal of Fourier Analysis and Applications,
Vol. 19,
Issue. 4,
p.
762.
Anand, Akash
and
Chavan, Sameer
2017.
Module tensor product of subnormal modules need not be subnormal.
Journal of Functional Analysis,
Vol. 272,
Issue. 11,
p.
4752.
Cárcamo, Javier
2017.
Maps Preserving Moment Sequences.
Journal of Theoretical Probability,
Vol. 30,
Issue. 1,
p.
212.
Anand, Akash
and
Chavan, Sameer
2017.
A Moment Problem and Joint q-Isometry Tuples.
Complex Analysis and Operator Theory,
Vol. 11,
Issue. 4,
p.
785.
Lin, Gwo Dong
2019.
On powers of the Catalan number sequence.
Discrete Mathematics,
Vol. 342,
Issue. 7,
p.
2139.
Reza, Md. Ramiz
and
Zhang, Genkai
2019.
Hausdorff Moment Sequences Induced by Rational Functions.
Complex Analysis and Operator Theory,
Vol. 13,
Issue. 8,
p.
4117.
Berg, Christian
and
Pedersen, Henrik L.
2023.
A Family of Horn-Bernstein Functions.
Experimental Mathematics,
Vol. 32,
Issue. 3,
p.
505.
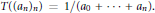 $T\left( {{\left( {{a}_{n}} \right)}_{n}} \right)\,=\,1/\left( {{a}_{0}}\,+\cdots +\,{{a}_{n}} \right).$ We give some examples of Hausdorff moment sequences arising from the transformations and provide the corresponding measures: one of these sequences is the reciprocal of the harmonic numbers
$T\left( {{\left( {{a}_{n}} \right)}_{n}} \right)\,=\,1/\left( {{a}_{0}}\,+\cdots +\,{{a}_{n}} \right).$ We give some examples of Hausdorff moment sequences arising from the transformations and provide the corresponding measures: one of these sequences is the reciprocal of the harmonic numbers 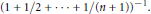 ${{\left( 1+1/2\,+\cdots +\,1/\left( n+1 \right) \right)}^{-1}}.$
${{\left( 1+1/2\,+\cdots +\,1/\left( n+1 \right) \right)}^{-1}}.$