Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Guardo, Elena
Harbourne, Brian
and
Van Tuyl, Adam
2013.
Asymptotic resurgences for ideals of positive dimensional subschemes of projective space.
Advances in Mathematics,
Vol. 246,
Issue. ,
p.
114.
Guardo, Elena
Harbourne, Brian
and
Van Tuyl, Adam
2013.
Fat lines in P3: Powers versus symbolic powers.
Journal of Algebra,
Vol. 390,
Issue. ,
p.
221.
Baczyńska, Magdalena
Dumnicki, Marcin
Habura, Agata
Malara, Grzegorz
Pokora, Piotr
Szemberg, Tomasz
Szpond, Justyna
and
Tutaj-Gasińska, Halszka
2014.
Points fattening on P1×P1 and symbolic powers of bi-homogeneous ideals.
Journal of Pure and Applied Algebra,
Vol. 218,
Issue. 8,
p.
1555.
Dumnicki, Marcin
Harbourne, Brian
Szemberg, Tomasz
and
Tutaj-Gasińska, Halszka
2014.
Linear subspaces, symbolic powers and Nagata type conjectures.
Advances in Mathematics,
Vol. 252,
Issue. ,
p.
471.
Guardo, Elena
and
Van Tuyl, Adam
2015.
Arithmetically Cohen-Macaulay Sets of Points in P^1 x P^1.
p.
71.
Guardo, Elena
and
Van Tuyl, Adam
2015.
Arithmetically Cohen-Macaulay Sets of Points in P^1 x P^1.
p.
117.
Bocci, Cristiano
Cooper, Susan
Guardo, Elena
Harbourne, Brian
Janssen, Mike
Nagel, Uwe
Seceleanu, Alexandra
Tuyl, Adam Van
and
Vu, Thanh
2016.
The Waldschmidt constant for squarefree monomial ideals.
Journal of Algebraic Combinatorics,
Vol. 44,
Issue. 4,
p.
875.
Ramos, Zaqueu
and
Simis, Aron
2017.
Homaloidal nets and ideals of fat points II: Subhomaloidal nets.
International Journal of Algebra and Computation,
Vol. 27,
Issue. 06,
p.
677.
Favacchio, Giuseppe
and
Guardo, Elena
2017.
The Minimal Free Resolution of Fat Almost Complete Intersections in ℙ1 × ℙ1.
Canadian Journal of Mathematics,
Vol. 69,
Issue. 6,
p.
1274.
Dao, Hailong
De Stefani, Alessandro
Grifo, Eloísa
Huneke, Craig
and
Núñez-Betancourt, Luis
2018.
Singularities and Foliations. Geometry, Topology and Applications.
Vol. 222,
Issue. ,
p.
387.
Cooper, Susan
Fatabbi, Giuliana
Guardo, Elena
Lorenzini, Anna
Migliore, Juan
Nagel, Uwe
Seceleanu, Alexandra
Szpond, Justyna
and
Tuyl, Adam Van
2020.
Symbolic powers of codimension two Cohen-Macaulay ideals.
Communications in Algebra,
Vol. 48,
Issue. 11,
p.
4663.
Favacchio, Giuseppe
and
Migliore, Juan
2021.
The ACM property for unions of lines in P1×P2.
Journal of Pure and Applied Algebra,
Vol. 225,
Issue. 11,
p.
106739.
Harbourne, B.
2021.
Commutative Algebra.
p.
445.
Dumnicki, Marcin
Harbourne, Brian
Roé, Joaquim
Szemberg, Tomasz
and
Tutaj-Gasińska, Halszka
2021.
Unexpected surfaces singular on lines in $${\mathbb {P}}^{3}$$.
European Journal of Mathematics,
Vol. 7,
Issue. 2,
p.
570.
Mandal, Mousumi
and
Kumar Pradhan, Dipak
2021.
Symbolic powers in weighted oriented graphs.
International Journal of Algebra and Computation,
Vol. 31,
Issue. 03,
p.
533.
Ballico, Edoardo
Favacchio, Giuseppe
Guardo, Elena
Milazzo, Lorenzo
and
Thomas, Abu Chackalamannil
2021.
Steiner Configurations Ideals: Containment and Colouring.
Mathematics,
Vol. 9,
Issue. 3,
p.
210.
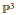 ${{\mathbb{P}}^{3}}$ that can also be viewed as points in
${{\mathbb{P}}^{3}}$ that can also be viewed as points in 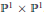 ${{\mathbb{P}}^{1}}\times {{\mathbb{P}}^{1}}$ . We also obtain results on the closely related problem, studied by Hochster and by Li and Swanson, of determining situations for which each symbolic power of an ideal is an ordinary power.
${{\mathbb{P}}^{1}}\times {{\mathbb{P}}^{1}}$ . We also obtain results on the closely related problem, studied by Hochster and by Li and Swanson, of determining situations for which each symbolic power of an ideal is an ordinary power.
