Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Stephenson, R. M.
1978.
Near compactness and separability of symmetrizable spaces.
Proceedings of the American Mathematical Society,
Vol. 68,
Issue. 1,
p.
108.
Davis, S.W.
Gruenhage, G.
and
Nyikos, P.J.
1978.
Gσ-sets in symmetrizable and related spaces.
General Topology and its Applications,
Vol. 9,
Issue. 3,
p.
253.
Davis, S. W.
and
Stephenson, R. M.
1979.
Separability and minimal weak base topologies.
Proceedings of the American Mathematical Society,
Vol. 74,
Issue. 2,
p.
371.
Stephenson, R.M.
1987.
Moore-closed and first countable feebly compact extension spaces.
Topology and its Applications,
Vol. 27,
Issue. 1,
p.
11.
Tanaka, Yoshio
2005.
On products of k-spaces.
Topology and its Applications,
Vol. 146-147,
Issue. ,
p.
593.
Liu, Chuan
and
Tanaka, Yoshio
2007.
Open Problems in Topology II.
p.
23.
Arhangel'skii, A.V.
2007.
Locally compact spaces of countable core and Alexandroff compactification.
Topology and its Applications,
Vol. 154,
Issue. 3,
p.
625.
Tanaka, Yoshio
2009.
Products of symmetric spaces, and k -networks.
Topology and its Applications,
Vol. 156,
Issue. 5,
p.
926.
Liu, Xin
Liu, Chuan
and
Lin, Shou
2019.
Strict Pytkeev networks with sensors and their applications in topological groups.
Topology and its Applications,
Vol. 258,
Issue. ,
p.
58.
Lin, Shou
and
Zhang, Jing
2024.
Recent Progress on Point-Countable Covers and Sequence-Covering Mappings.
Axioms,
Vol. 13,
Issue. 10,
p.
728.

 -, and Weakly First Countable Spaces
-, and Weakly First Countable Spaces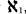 , then
, then 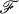 -space
-space 