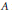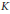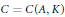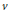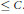Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Akbary, Amir
Gun, Sanoli
and
Murty, M. Ram
2018.
Geometry, Algebra, Number Theory, and Their Information Technology Applications.
Vol. 251,
Issue. ,
p.
1.
Zaman, Asif
2018.
The least unramified prime which does not split completely.
Forum Mathematicum,
Vol. 30,
Issue. 3,
p.
651.
Ge, Zhenchao
Milinovich, Micah B.
and
Pollack, Paul
2019.
A note on the least prime that splits completely in a nonabelian Galois number field.
Mathematische Zeitschrift,
Vol. 292,
Issue. 1-2,
p.
183.