Hostname: page-component-cb9f654ff-p5m67 Total loading time: 0 Render date: 2025-08-21T21:44:29.982Z Has data issue: false hasContentIssue false
  • English
  • Français

Tree densities in sparse graph classes

Part of: Graph theory

Published online by Cambridge University Press:  29 June 2021

Tony Huynh  and
David R. Wood
Tony Huynh*
Affiliation:
School of Mathematics, Monash University, Melbourne, Australia e-mail: david.wood@monash.edu
David R. Wood
Affiliation:
School of Mathematics, Monash University, Melbourne, Australia e-mail: david.wood@monash.edu
*
e-mail: tony.bourbaki@gmail.com
Get access Rights & Permissions [Opens in a new window]

Abstract

What is the maximum number of copies of a fixed forest T in an n-vertex graph in a graph class 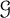$\mathcal {G}$ as 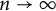$n\to \infty $? We answer this question for a variety of sparse graph classes 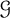$\mathcal {G}$. In particular, we show that the answer is 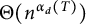$\Theta (n^{\alpha _{d}(T)})$ where 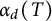$\alpha _{d}(T)$ is the size of the largest stable set in the subforest of T induced by the vertices of degree at most d, for some integer d that depends on 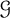$\mathcal {G}$. For example, when 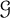$\mathcal {G}$ is the class of k-degenerate graphs then 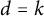$d=k$; when 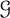$\mathcal {G}$ is the class of graphs containing no 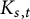$K_{s,t}$-minor (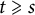$t\geqslant s$) then 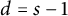$d=s-1$; and when 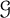$\mathcal {G}$ is the class of k-planar graphs then 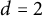$d=2$. All these results are in fact consequences of a single lemma in terms of a finite set of excluded subgraphs.

Keywords

Extremal combinatoricstreesgraph minorssparsity

MSC classification

Primary: 90C35: Programming involving graphs or networks
Secondary: 05C05: Trees 05C83: Graph minors

Information

Type
Article
Information
Canadian Journal of Mathematics , Volume 74 , Issue 5 , October 2022 , pp. 1385 - 1404
Check for updates
Copyright
© Canadian Mathematical Society 2021

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

Footnotes

Research supported by the Australian Research Council.

References

Alameddine, A. F., On the number of cycles of length  $4$  in a maximal planar graph . J. Graph Theory 4(1980), no. 4, 417–422.CrossRefGoogle Scholar
Alexander, J., Cutler, J., and Mink, T., Independent sets in graphs with given minimum degree. Electron. J. Combin. 19(2012), no. 3, P37.CrossRefGoogle Scholar
Alon, N. and Caro, Y., On the number of subgraphs of prescribed type of planar graphs with a given number of vertices . In: Convexity and graph theory, North-Holland Math. Stud., 86, North-Holland, 1984, pp. 25–36.Google Scholar
Alon, N., Kostochka, A., and Shikhelman, C., Many cliques in  $H$ -free subgraphs of random graphs . J. Comb. 9(2018), no. 4, 567–597.Google Scholar
Alon, N. and Shikhelman, C., Many $T$ copies in  $H$ -free graphs . J. Combin. Theory Ser. B 121(2016), 146–172.CrossRefGoogle Scholar
Alon, N. and Shikhelman, C., $H$ -free subgraphs of dense graphs maximizing the number of cliques and their blow-ups . Discrete Math. 342(2019), no. 4, 988–996.CrossRefGoogle Scholar
Alweiss, R., Lovett, S., Wu, K., and Zhang, J., Improved bounds for the sunflower lemma . In: Proc. 52nd Annual ACM Symp. on Theory of Computing (STOC 2020), 2020, pp. 624–630.CrossRefGoogle Scholar
Bae, S. W., Baffier, J.-F., Chun, J., Eades, P., Eickmeyer, K., Grilli, L., Hong, S.-H., Korman, M., Montecchiani, F., Rutter, I., and Tóth, C. D., Gap-planar graphs. Theor. Comput. Sci. 745(2018), 36–52.CrossRefGoogle Scholar
Bell, T., Chueluecha, S., and Warnke, L., Note on sunflowers. Discrete Math. 344(2021), no. 7, 112367.CrossRefGoogle Scholar
Biedl, T. and Wilkinson, D. F., Bounded-degree independent sets in planar graphs. Theory Comput. Syst. 38(2005), no. 3, 253–278.CrossRefGoogle Scholar
Bienstock, D., Robertson, N., Seymour, P. D., and Thomas, R., Quickly excluding a forest. J. Combin. Theory Ser. B 52(1991), no. 2, 274–283.CrossRefGoogle Scholar
Bose, P., Dujmović, V., and Wood, D. R., Induced subgraphs of bounded treewidth and bounded degree. Contrib. Discrete Math. 1(2006), no. 1, 88–105.Google Scholar
Bose, P., Smid, M., and Wood, D. R., Light edges in degree-constrained graphs. Discrete Math. 282(2004), nos. 1–3, 35–41. MR:2059504.Google Scholar
Chase, Z., The maximum number of triangles in a graph of given maximum degree. Adv. Combin. (2020), 5–10.Google Scholar
Chen, Z.-Z., Approximation algorithms for independent sets in map graphs. J. Algorithms 41(2001), no. 1, 20–40.CrossRefGoogle Scholar
Chen, Z.-Z., New bounds on the edge number of a $k$ -map graph . J. Graph Theory 55(2007), no. 4, 267–290.CrossRefGoogle Scholar
Chen, Z.-Z., Grigni, M., and Papadimitriou, C. H., Map graphs. J. ACM. 49(2002), no. 2, 127–138.CrossRefGoogle Scholar
Conway, J. H. and Gordon, C. M., Knots and links in spatial graphs. J. Graph Theory 7(1983), 445–453.CrossRefGoogle Scholar
Cutler, J. and Radcliffe, A. J., Extremal problems for independent set enumeration. Electron. J. Combin. 18(2011), no. 1, P169.CrossRefGoogle Scholar
Cutler, J. and Radcliffe, A. J., The maximum number of complete subgraphs in a graph with given maximum degree. J. Combin. Theory Ser. B 104(2014), 60–71.CrossRefGoogle Scholar
Cutler, J. and Radcliffe, A. J., The maximum number of complete subgraphs of fixed size in a graph with given maximum degree. J. Graph Theory 84(2017), no. 2, 134–145.CrossRefGoogle Scholar
de Mendez, P. O., Oum, S.-i., and Wood, D. R., Defective colouring of graphs excluding a subgraph or minor. Combinatorica 39(2019), no. 2, 377–410.CrossRefGoogle Scholar
de Verdière, Y. C., Sur un nouvel invariant des graphes et un critère de planarité. J. Combin. Theory Ser. B 50(1990), no. 1, 11–21.CrossRefGoogle Scholar
de Verdière, Y. C., On a new graph invariant and a criterion for planarity. In: Graph structure theory, Contemp. Math., 147, Amer. Math. Soc., 1993, pp. 137–147.Google Scholar
Demaine, E. D., Fomin, F. V., Hajiaghayi, M., and Thilikos, D. M., Fixed-parameter algorithms for  $\left(k,r\right)$ -center in planar graphs and map graphs . ACM Trans. Algorithms 1(2005), no. 1, 33–47.CrossRefGoogle Scholar
Dujmović, V., Eppstein, D., and Wood, D. R., Structure of graphs with locally restricted crossings. SIAM J. Discrete Math. 31(2017), no. 2, 805–824.CrossRefGoogle Scholar
Dujmović, V., Fijavž, G., Joret, G., Sulanke, T., and Wood, D. R., On the maximum number of cliques in a graph embedded in a surface. European J. Combin. 32(2011), no. 8, 1244–1252.Google Scholar
Dujmović, V., Morin, P., and Wood, D. R., Graph product structure for non-minor-closed classes. 2019. arXiv:1907.05168 Google Scholar
Eckhoff, J., The maximum number of triangles in a  ${K}_4$ -free graph . Discrete Math. 194(1999), nos. 1–3, 95–106.CrossRefGoogle Scholar
Eckhoff, J., A new Turán-type theorem for cliques in graphs. Discrete Math. 282(2004), nos. 1–3, 113–122.CrossRefGoogle Scholar
Engbers, J. and Galvin, D., Counting independent sets of a fixed size in graphs with a given minimum degree. J. Graph Theory 76(2014), no. 2, 149–168.CrossRefGoogle Scholar
Eppstein, D., Connectivity, graph minors, and subgraph multiplicity. J. Graph Theory 17(1993), no. 3, 409–416.CrossRefGoogle Scholar
Eppstein, D. and Gupta, S., Crossing patterns in nonplanar road networks. In: Proc. 25th ACM SIGSPATIAL Int’l Conf. on Advances in Geographic Information Systems, 40, 2017, pp. 1–9.Google Scholar
Erdős, P. and Rado, R., Intersection theorems for systems of sets. J. London Math. Soc. Second Ser. 35(1960), no. 1, 85–90.CrossRefGoogle Scholar
Erdős, P. and Stone, A. H., On the structure of linear graphs. Bull. Amer. Math. Soc. 52(1946), 1087–1091.CrossRefGoogle Scholar
Ergemlidze, B., Methuku, A., Salia, N., and Győri, E., A note on the maximum number of triangles in a  ${C}_5$ -free graph . J. Graph Theory 90(2019), no. 3, 227–230.CrossRefGoogle Scholar
Fiorini, S., Joret, G., Theis, D. O., and Wood, D. R., Small minors in dense graphs. Eur. J. Combin. 33(2012), no. 6, 1226–1245.CrossRefGoogle Scholar
Fisher, D. C. and Ryan, J., Conjectures on the number of complete subgraphs. In: Proc. 20th Southeastern Conf. on Combinatorics, Graph Theory, and Computing, 70, pp. 217–219. 1990.Google Scholar
Fisher, D. C. and Ryan, J., Bounds on the number of complete subgraphs. Discrete Math. 103(1992), no. 3, 313–320.CrossRefGoogle Scholar
Foisy, J., Intrinsically knotted graphs. J. Graph Theory 39(2002), no. 3, 178–187.CrossRefGoogle Scholar
Fomin, F. V., Lokshtanov, D., and Saurabh, S., Bidimensionality and geometric graphs. In: Proc. 23rd Annual ACM-SIAM Symp. on Discrete Algorithms, 2012, pp. 1563–1575.CrossRefGoogle Scholar
Fomin, F. V., Oum, S.-I., and Thilikos, D. M., Rank-width and tree-width of  $H$ -minor-free graphs . Eur. J. Combin. 31(2010), no. 7, 1617–1628.CrossRefGoogle Scholar
Fox, J. and Wei, F., On the number of cliques in graphs with a forbidden minor. J. Combin. Theory Ser. B 126(2017), 175–197.CrossRefGoogle Scholar
Fox, J. and Wei, F., On the number of cliques in graphs with a forbidden subdivision or immersion. SIAM J. Discrete Math. 34(2020), no. 4, 2556–2582.CrossRefGoogle Scholar
Frohmader, A., A Kruskal-Katona type theorem for graphs. J. Combin. Theory Ser. A 117(2010), no. 1, 17–37.CrossRefGoogle Scholar
Galvin, D., Two problems on independent sets in graphs. Discrete Math. 311(2011), no. 20, 2105–2112.CrossRefGoogle Scholar
Gan, W., Loh, P.-S., and Sudakov, B., Maximizing the number of independent sets of a fixed size. Combin. Probab. Comput. 24(2015), no. 3, 521–527.CrossRefGoogle Scholar
Gerbner, D., Győri, E., Methuku, A., and Vizer, M., Generalized Turán problems for even cycles. J. Combin. Theory Ser. B 145(2020), 169–213.CrossRefGoogle Scholar
Gerbner, D., Methuku, A., and Vizer, M., Generalized Turán problems for disjoint copies of graphs. Discrete Math. 342(2019), no. 11, 3130–3141.CrossRefGoogle Scholar
Gerbner, D. and Palmer, C., Counting copies of a fixed subgraph in  $F$ -free graphs . Eur. J. Combin. 82(2019), 103001.CrossRefGoogle Scholar
Goldberg, F. and Berman, A., On the Colin de Verdière number of graphs. Linear Algebra Appl. 434(2011), no. 7, 1656–1662.CrossRefGoogle Scholar
Goldberg, N., Mattman, T. W., and Naimi, R., Many, many more intrinsically knotted graphs. Algebr. Geom. Topol. 14(2014), no. 3, 1801–1823.CrossRefGoogle Scholar
Győri, E., Paulos, A., Salia, N., Tompkins, C., and Zamora, O., The maximum number of paths of length three in a planar graph. Preprint 2019. arXiv:1909.13539 Google Scholar
Győri, E., Paulos, A., Salia, N., Tompkins, C., and Zamora, O., The maximum number of pentagons in a planar graph. Preprint 2019. arXiv:1909.13532 Google Scholar
Győri, E., Salia, N., Tompkins, C., and Zamora, O., The maximum number of  ${P}_{\ell }$  copies in  ${P}_k$ -free graphs . Discrete Math. Theor. Comput. Sci. 21(2019), 14.Google Scholar
Harant, J., Horňák, M., and Skupień, Z., Separating 3-cycles in plane triangulations. Discrete Math. 239(2001), nos. 1–3, 127–136.CrossRefGoogle Scholar
Harvey, D. J. and Wood, D. R., Parameters tied to treewidth. J. Graph Theory 84(2017), no. 4, 364–385.CrossRefGoogle Scholar
Hedman, B., The maximum number of cliques in dense graphs. Discrete Math. 54(1985), no. 2, 161–166.CrossRefGoogle Scholar
Huynh, T., Joret, G., and Wood, R. D., Subgraph densities in a surface, Preprint, 2020, arXiv:2003.13777 Google Scholar
Kahn, J., An entropy approach to the hard-core model on bipartite graphs. Combin. Probab. Comput. 10(2001), no. 3, 219–237.CrossRefGoogle Scholar
Khadzhiivanov, N. and Nenov, N., Sharp estimates of the highest number of cliques of a graph. Annuaire Univ. Sofia Fac. Math. Méc. 70(1975/76), 23–26.Google Scholar
Kirsch, R. and Radcliffe, A. J., Many triangles with few edges. Electron. J. Combin. 26(2019), no. 2, P2.36.CrossRefGoogle Scholar
Kobourov, S. G., Liotta, G., and Montecchiani, F., An annotated bibliography on 1-planarity. Comput. Sci. Rev. 25(2017), 49–67.Google Scholar
König, D., Theorie der endlichen und unendlichen Graphen . Kombinatorische Topologie der Streckenkomplexe, Akademische Verlagsgesellschaft, Leipzig, 1936.Google Scholar
Kostochka, A. V., Lower bound of the Hadwiger number of graphs by their average degree. Combinatorica 4(1984), no. 4, 307–316.CrossRefGoogle Scholar
Lee, C. and Oum, S.-I., Number of cliques in graphs with a forbidden subdivision. SIAM J. Disc. Math. 29(2015), no. 4, 1999–2005.CrossRefGoogle Scholar
Letzter, S., Many  $H$ -copies in graphs with a forbidden tree . SIAM J. Discrete Math 33(2019), no. 4, 2360–2368.Google Scholar
Louis Hakimi, S., On the degrees of the vertices of a directed graph. J. Franklin Inst. 279(1965), 290–308.Google Scholar
Hakimi, S. Louis and Schmeichel, E. F., On the number of cycles of length  $k$  in a maximal planar graph . J. Graph Theory 3(1979), no. 1, 69–86.CrossRefGoogle Scholar
Hakimi, S. Louis and Schmeichel, E. F., Bounds on the number of cycles of length three in a planar graph. Israel J. Math. 41(1982), nos. 1–2, 161–180.CrossRefGoogle Scholar
Luo, R., The maximum number of cliques in graphs without long cycles. J. Combin. Theory Ser. B 128(2018), 219–226.CrossRefGoogle Scholar
Ma, J. and Qiu, Y., Some sharp results on the generalized Turán numbers. Eur. J. Combin. 84(2020), 103026.Google Scholar
Mader, W., Homomorphiesätze für Graphen. Math. Ann. 178(1968), 154–168.CrossRefGoogle Scholar
Mohar, B. and Thomassen, C., Graphs on surfaces . Johns Hopkins University Press, 2001.Google Scholar
Montgomery, R., Logarithmically small minors and topological minors. J. London Math. Soc. 91(2015), no. 1, 71–88.CrossRefGoogle Scholar
Nešetřil, J. and de Mendez, P. O., How many  $F$ ’s are there in  $G$ ? Eur. J. Combin. 32(2011), no. 7, 1126–1141.CrossRefGoogle Scholar
Nešetřil, J. and de Mendez, P. O., Sparsity. Algorithms and Combinatorics, 28, Springer, 2012.CrossRefGoogle Scholar
Nešetřil, J. and de Mendez, P. O., On low tree-depth decompositions. Graphs Combin 31(2015), no. 6, 1941–1963.Google Scholar
Norine, S., Seymour, P., Thomas, R., and Wollan, P., Proper minor-closed families are small. J. Combin. Theory Ser. B 96(2006), no. 5, 754–757.Google Scholar
Pach, J. and Tóth, G., Recognizing string graphs is decidable. Discrete Comput. Geom. 28(2002), no. 4, 593–606.CrossRefGoogle Scholar
Papadimitriou, C. H. and Yannakakis, M., The clique problem for planar graphs. Inform. Process. Lett. 13(1981), nos. 4–5, 131–133.Google Scholar
Petingi, L. and Rodriguez, J., A new proof of the Fisher-Ryan bounds for the number of cliques of a graph. In: Proc. 31st Southeastern Int’l Conf. on Combinatorics, Graph Theory and Computing, Congr. Numer., 146, 2000, pp. 143–146.Google Scholar
Ramírez Alfonsín, J. L., Knots and links in spatial graphs: a survey. Discrete Math 302(2005), nos. 1–3, 225–242.CrossRefGoogle Scholar
Reed, B. and Wood, D. R., A linear time algorithm to find a separator in a graph excluding a minor. ACM Trans. Algorithms 5(2009), no. 4, 39.Google Scholar
Reed, B. A., Tree width and tangles: a new connectivity measure and some applications. In: Bailey, R. A. (ed.), Surveys in combinatorics, London Math. Soc. Lecture Note Ser., 241, Cambridge Univ. Press, 1997, pp. 87–162.Google Scholar
Ringel, G., Das Geschlecht des vollständigen paaren Graphen. Abh. Math. Sem. Univ. Hamburg 28(1965), 139–150.CrossRefGoogle Scholar
Robertson, N., Seymour, P., and Thomas, R., A survey of linkless embeddings . In: Robertson, N. and Seymour, P. (eds.), Graph structure theory, Proc. AMS-IMS-SIAM Joint Summer Research Conf. on Graph Minors, Contemporary Math., 147, Amer. Math. Soc., 1993, pp. 125–136.Google Scholar
Robertson, N., Seymour, P., and Thomas, R., Sachs’ linkless embedding conjecture. J. Combin. Theory Ser. B 64(1995), 185–227.Google Scholar
Sachs, H., On a spatial analogue of Kuratowski’s theorem on planar graphs — an open problem. In: Borowiecki, M., Kennedy, J. W., and Syslo, M. M. (eds.), Proc. Conf. on Graph Theory, Lecture Notes in Math., 1018, Springer, 1983, pp. 230–241.Google Scholar
Schrijver, A., Minor-monotone graph invariants. In: Surveys in combinatorics, London Math. Soc. Lecture Note Ser., 241, Cambridge Univ. Press, 1997, pp. 163–196.CrossRefGoogle Scholar
Shapira, A. and Sudakov, B., Small complete minors above the extremal edge density. Combinatorica 35(2015), no. 1, 75–94.CrossRefGoogle Scholar
Shimabara, M., Knots in certain spatial graphs. Tokyo J. Math 11(1988), no. 2, 405–413.CrossRefGoogle Scholar
Thomason, A., An extremal function for contractions of graphs. Math. Proc. Cambridge Philos. Soc 95(1984), no. 2, 261–265.CrossRefGoogle Scholar
Turán, P., On an extremal problem in graph theory. Mat. Fiz. Lapok 48(1941), 436–452.Google Scholar
van Batenburg, W. C., Huynh, T., Joret, G., and Raymond, J.-F., A tight Erdős-Pósa function for planar minors. Adv. Combin. 2(2019).Google Scholar
van der Holst, H., Lovász, L., and Schrijver, A., The Colin de Verdière graph parameter. In: Graph theory and combinatorial biology, Bolyai Soc. Math. Stud., 7, János Bolyai Math. Soc., 1999, pp. 29–85.Google Scholar
Wood, D. R., On the maximum number of cliques in a graph. Graphs Combin. 23(2007), no. 3, 337–352.CrossRefGoogle Scholar
Wormald, N. C., On the frequency of  $3$ -connected subgraphs of planar graphs . Bull. Austral. Math. Soc. 34(1986), no. 2, 309–317.CrossRefGoogle Scholar
Zykov, A. A., On some properties of linear complexes. Mat. Sbornik N.S. 24(1949), no. 66, 163–188.Google Scholar