Hostname: page-component-8448b6f56d-t5pn6 Total loading time: 0 Render date: 2024-04-19T16:14:50.355Z Has data issue: false hasContentIssue false
  • English
  • Français

Two-Dimensional Linear Groups Over Local Rings

Published online by Cambridge University Press:  20 November 2018

Norbert H. J. Lacroix
Norbert H. J. Lacroix*
Affiliation:
Université Laval, Québec, Québec
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The problem of classifying the normal subgroups of the general linear group over a field was solved in the general case by Dieudonné (see 2 and 3). If we consider the problem over a ring, it is trivial to see that there will be more normal subgroups than in the field case. Klingenberg (4) has investigated the situation over a local ring and has shown that they are classified by certain congruence groups which are determined by the ideals in the ring.

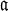Klingenberg's solution roughly goes as follows. To a given ideal , attach certain congruence groups 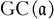and 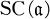. Next, assign a certain ideal (called the order) to a given subgroup G. The main result states that if G is normal with order a, then 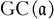≧ G ≧ 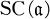, that is, G satisfies the so-called ladder relation at 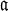; conversely, if G satisfies the ladder relation at 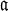, then G is normal and has order .

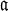Type
Research Article
Information
Canadian Journal of Mathematics , Volume 21 , 1969 , pp. 106 - 135
Copyright
Copyright © Canadian Mathematical Society 1969

References

1. Artin, E., Geometric algebra (Interscience, New York, 1957).Google Scholar
2. Dieudonné, J., Les déterminants sur un corps non commutatif, Bull. Soc. Math. France 71 (1943), 27–45.Google Scholar
3. Dieudonné, J., La géométrie des groupes classiques, 2e éd. (Springer-Verlag, Berlin, 1963).Google Scholar
4. Klingenberg, W., Lineare Gruppen ilber lokalen Ringen, Amer. J. Math. 83 (1961), 137–153.Google Scholar
5. Ledermann, W., Introduction to the theory of finite groups (Oliver and Boyd, Edinburgh, 1961).Google Scholar
6. O'Meara, O. T., Introduction to quadratic forms (Springer-Verlag, Berlin, 1963).Google Scholar
7. Zassenhaus, H. J., The theory of groups, 2nd. ed. (Chelsea, New York, 1958).Google Scholar