Article contents
Uniformly Continuous Functionals andM-Weakly Amenable Groups
Published online by Cambridge University Press: 20 November 2018
Abstract
Let  $G$ be a locally compact group. Let
$G$ be a locally compact group. Let 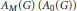 ${{A}_{M}}\left( G \right)\,\left( {{A}_{0}}\left( G \right) \right)$ denote the closure of
${{A}_{M}}\left( G \right)\,\left( {{A}_{0}}\left( G \right) \right)$ denote the closure of 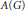 $A\left( G \right)$ , the Fourier algebra of
$A\left( G \right)$ , the Fourier algebra of  $G$ in the space of bounded (completely bounded) multipliers of
$G$ in the space of bounded (completely bounded) multipliers of 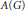 $A\left( G \right)$ . We call a locally compact group
$A\left( G \right)$ . We call a locally compact group 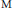 $\text{M}$ -weakly amenable if
$\text{M}$ -weakly amenable if 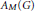 ${{A}_{M}}\left( G \right) $ has a bounded approximate identity. We will show that when
${{A}_{M}}\left( G \right) $ has a bounded approximate identity. We will show that when  $G$ is
$G$ is 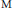 $\text{M}$ -weakly amenable, the algebras
$\text{M}$ -weakly amenable, the algebras 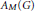 ${{A}_{M}}\left( G \right) $ and
${{A}_{M}}\left( G \right) $ and 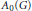 ${{A}_{0}}\left( G \right)$ have properties that are characteristic of the Fourier algebra of an amenable group. Along the way we show that the sets of topologically invariant means associated with these algebras have the same cardinality as those of the Fourier algebra.
${{A}_{0}}\left( G \right)$ have properties that are characteristic of the Fourier algebra of an amenable group. Along the way we show that the sets of topologically invariant means associated with these algebras have the same cardinality as those of the Fourier algebra.
Keywords
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 2013
References
- 4
- Cited by

