Hostname: page-component-7dd5485656-kp629 Total loading time: 0 Render date: 2025-10-30T18:36:19.523Z Has data issue: false hasContentIssue false
  • English
  • Français

Weak Semiprojectivity in Purely Infinite Simple C*-Algebras

Published online by Cambridge University Press:  20 November 2018

Huaxin Lin
Huaxin Lin*
Affiliation:
Department of Mathematics, East China Normal University, Shangai, P.R. China, and Department of Mathematics, University of Oregon, Eugene, OR 97403-1222, U.S.A. email: hlin@uoregon.edu
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 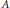$A$ be a separable amenable purely infinite simple 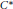${{C}^{*}}$ -algebra which satisfies the Universal Coefficient Theorem. We prove that 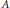$A$ is weakly semiprojective if and only if 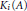${{K}_{i}}(A\text{)}$ is a countable direct sum of finitely generated groups 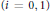$\left( i\,=\,0,\,1 \right)$ . Therefore, if 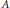$A$ is such a 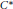${{C}^{*}}$ -algebra, for any 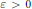$\varepsilon \,>\,0$ and any finite subset 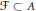$\mathcal{F}\,\subset \,A$ there exist 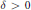$\delta \,>\,0$ and a finite subset 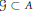$G\,\subset \,A$ satisfying the following: for any contractive positive linear map 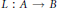$L\,:\,A\,\to \,B$ (for any 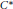${{C}^{*}}$ -algebra $B$ ) with 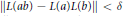$||L\left( ab \right)\,-\,L\left( a \right)L\left( b \right)||\,<\,\delta$ for 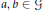$a,\,b\,\in \,\mathcal{G}$ there exists a homomorphism 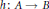$h:\,A\,\to \,B$ such that 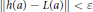$||\,h\left( a \right)\,-\,L\left( a \right)||\,<\,\varepsilon$ for 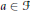$a\,\in \,\mathcal{F}$ .

Keywords

46L0546L80weakly semiprojectivepurely infinite simpleC*-algebras

Information

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 59 , Issue 2 , 01 April 2007 , pp. 343 - 371
Copyright
Copyright © Canadian Mathematical Society 2007

References

[BG] Bartle, R. G. and Graves, L. M., Mappings between function spaces. Trans. Amer. Math. Soc. 72(1952), 400–413.Google Scholar
[BEEK] Bratteli, O., Elliott, G. A., Evans, D. and Kishimoto, A., On the classification of C*-algebras of real rank zero. III. The infinite case. In: Operator algebras and their applications, Fields Inst. Commun. 20, American Mathematical Society, Providence, RI, 1998, pp. 11–72.Google Scholar
[BSKR] Bratteli, O., Størmer, E., Kishimoto, A., and Rørdam, M., The crossed product of a UHF algebra by a shift. Ergodic Theory Dynam. Systems 13(1993), no. 4, 615–626.Google Scholar
[Br] Brown, L. G., Stable isomorphism of hereditary subalgebras of C*-algebras. Pacific J. Math. 71(1977), no. 2, 335–348.Google Scholar
[Cu1] Cuntz, J., Simple C*-algebras generated by isometries, Comm. Phys. 57(1977), 173–185.Google Scholar
[Cu2] Cuntz, J., K-theory for certain C*-algebras, Ann. of Math. 113(1981), 181–197.Google Scholar
[DE] Dadarlat, M. and Eilers, S., On the classification of nuclear C*-algebras. Proc. London Math. Soc. 85(2002), no. 1, 168–210.Google Scholar
[DL] Dadarlat, M. and Loring, T., A universal multi-coefficient theorem for the Kasparov groups. Duke J. Math. 84(1996), 355–377.Google Scholar
[ER] Elliott, G. A. and Rørdam, M., Classification of certain infinite simple C*-algebras. II. Comment. Math. Helvetici 70(1995), 615–638.Google Scholar
[GL1] Gong, G. and Lin, H., Almost multiplicative morphisms and almost commuting matrices. J. Operator Theory 40(1998), no. 2, 217–27.Google Scholar
[GL2] Gong, G. and Lin, H., Almost multiplicative morphisms and K-theory. Internat. J. Math. 11(2000), no. 8, 983–1000.Google Scholar
[H] Higson, N., A characterization of KK-theory. Pacific J. Math. 126(1987), 253–276.Google Scholar
[K] Kirchberg, E., The classification of purely infinite simple C*-algebras using Kasparov's theory, to appear in the Fields Institute Communication series.Google Scholar
[KP] Kirchberg, E. and Phillips, N. C., Embedding of exact C*-algebras in the Cuntz algebr. O2. J. Reine Angew. Math. 552(2000), 17–53.Google Scholar
[Ln1] Lin, H., Equivalent open projections and corresponding hereditary C*-subalgebras. J. London Math. Soc. 41(1990), no. 2, 295–301.Google Scholar
[Ln2] Lin, H., Almost commuting unitaries and classification of purely infinite simple C*-algebras. J. Funct. Anal. 155(1998), no. 1, 1–24.Google Scholar
[Ln3] Lin, H., Stable approximate unitary equivalence of homomorphisms. J. Operator Theory 47(2002), no. 2, 343–378.Google Scholar
[Ln4] Lin, H., Classification of simple tracially AF C*-algebras. Canad. J. Math. 53(2001), no. 1, 161–194.Google Scholar
[Ln5] Lin, H., An introduction to the classification of amenable C*-algebras. World Scientific Publishing, Riveredge, NJ, 2001.Google Scholar
[Ln6] Lin, H., An approximate universal coefficient theorem. Trans. Amer. Math. Soc. 357(2005), 3375–3405 (electronic).Google Scholar
[Ln7] Lin, H., A separable Brown-Douglas-Fillmore theorem and weak stability. Trans. Amer.Math. Soc. 356(2004), no. 7, 2889–2925.Google Scholar
[LP1] Lin, H. and Phillips, N. C., Classification of direct limits of even Cuntz-circle algebras. Mem. Amer. Math. Soc. 118(1995), no. 565.Google Scholar
[LP2] Lin, H. and Phillips, N. C., Approximate unitary equivalence of homomorphisms from . J. Reine Angew. Math. 464(1995), 173–186.Google Scholar
[Lo] Loring, T., Lifting solutions to perturbing problems in C*-algebras. Fields Institute Monographs 8, American Mathematical Society, Providence, RI, 1997.Google Scholar
[P1] Phillips, N. C., Approximate unitary equivalence of homomorphisms from odd Cuntz algebras. In: Operator Algebras and Their Applications. Fields Inst. Commun. 13, American Mathematical Society, Providence, RI, 1997, pp. 243–255.Google Scholar
[P2] Phillips, N. C., A classification theorem for nuclear purely infinite simple C*-algebras. Doc. Math. 5(2000), 49–114.Google Scholar
[Ro1] Rørdam, M., Classification of inductive limits of Cuntz algebras. J. Reine Angew. Math. 440(1993), 175–200.Google Scholar
[Ro2] Rørdam, M., Classification of certain infinite simple C*-algebras. J. Funct. Anal. 131(1995), no. 2, 415–458.Google Scholar
[Ro3] Rørdam, M., A short proof of Elliott's theorem. . C. R. Math. Rep. Acad. Sci. Canada 16(1994), no. 1, 31–36.Google Scholar
[Ro4] Rørdam, M., Classification of nuclear C*-algebras. in Operator Algebras, VII, Encyclopaedia of Mathematical Sciences, Springer-Verlag, Berlin, Heidelberg and New York, 2000.Google Scholar
[RS] Rosenberg, J. and Schochet, C., The Künneth theorem and the universal coefficient theorem for Kasparov's generalized functor. Duke Math. J. 55(1987), 431–474.Google Scholar
[S1] Schochet, C., Topological methods for C*-algebras. III. Axiomatic homology. Pacific J. Math. 114(1984), no. 2, 399–445.Google Scholar
[S2] Schochet, C., Topological methods for C*-algebras. IV. Mod p homology. Pacific J. Math. 114(1984), no. 2, 447–468.Google Scholar
[S3] Schochet, C., The fine structure of the Kasparov groups. I. Continuity of the KK-paring. J. Funct. Anal. 186(2001), no. 1, 25–61.Google Scholar
[Sp] Spielberg, J., Semiprojectivity of certain purely infinite C*-algebras. preprint, 2001.Google Scholar
[Sz] Szymanski, W., On semiprojectivity of C*-algebras of direct graphs. preprint 2001.Google Scholar
[Zh1] Zhang, S., Stable isomorphism of hereditary C*-subalgebras and stable equivalence of open projections. Proc. Amer. Math. Soc. 105(1989), no. 3, 677–682.Google Scholar