Article contents
Weighted Distribution of Low-lying Zeros of GL(2) 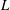 $L$-functions
$L$-functions
Published online by Cambridge University Press: 08 January 2019
Abstract
We show that if the zeros of an automorphic 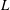 $L$-function are weighted by the central value of the
$L$-function are weighted by the central value of the 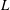 $L$-function or a quadratic imaginary base change, then for certain families of holomorphic GL(2) newforms, it has the effect of changing the distribution type of low-lying zeros from orthogonal to symplectic, for test functions whose Fourier transforms have sufficiently restricted support. However, if the
$L$-function or a quadratic imaginary base change, then for certain families of holomorphic GL(2) newforms, it has the effect of changing the distribution type of low-lying zeros from orthogonal to symplectic, for test functions whose Fourier transforms have sufficiently restricted support. However, if the 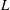 $L$-value is twisted by a nontrivial quadratic character, the distribution type remains orthogonal. The proofs involve two vertical equidistribution results for Hecke eigenvalues weighted by central twisted
$L$-value is twisted by a nontrivial quadratic character, the distribution type remains orthogonal. The proofs involve two vertical equidistribution results for Hecke eigenvalues weighted by central twisted 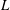 $L$-values. One of these is due to Feigon and Whitehouse, and the other is new and involves an asymmetric probability measure that has not appeared in previous equidistribution results for GL(2).
$L$-values. One of these is due to Feigon and Whitehouse, and the other is new and involves an asymmetric probability measure that has not appeared in previous equidistribution results for GL(2).
Keywords
Information
- Type
- Article
- Information
- Copyright
- © Canadian Mathematical Society 2018
Footnotes
This work was partially supported by grant #317659 from the Simons Foundation to author A. K. Section 3 is based in part on the University of Maine MA thesis of author C. R.
References
- 5
- Cited by

