Hostname: page-component-7dd5485656-g8tfn Total loading time: 0 Render date: 2025-10-30T22:48:08.274Z Has data issue: false hasContentIssue false
  • English
  • Français

Zeta Functions and ‘Kontsevich Invariants’ on Singular Varieties

Published online by Cambridge University Press:  20 November 2018

Willem Veys
Willem Veys*
Affiliation:
K. U. Leuven, Departement Wiskunde, Celestijnenlaan 200B, B–3001 Leuven, Belgium website: http://www.wis.kuleuven.ac.be/wis/algebra/veys.htm email: wim.veys@wis.kuleuven.ac.be
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 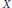$X$ be a nonsingular algebraic variety in characteristic zero. To an effective divisor on 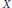$X$ Kontsevich has associated a certain motivic integral, living in a completion of the Grothendieck ring of algebraic varieties. He used this invariant to show that birational (smooth, projective) Calabi-Yau varieties have the same Hodge numbers. Then Denef and Loeser introduced the invariant motivic (Igusa) zeta function, associated to a regular function on 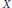$X$ , which specializes to both the classical 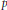$p$ -adic Igusa zeta function and the topological zeta function, and also to Kontsevich's invariant.

This paper treats a generalization to singular varieties. Batyrev already considered such a ‘Kontsevich invariant’ for log terminal varieties (on the level of Hodge polynomials of varieties instead of in the Grothendieck ring), and previously we introduced a motivic zeta function on normal surface germs. Here on any 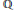$\mathbb{Q}$ -Gorenstein variety 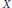$X$ we associate a motivic zeta function and a ‘Kontsevich invariant’ to effective 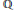$\mathbb{Q}$ -Cartier divisors on 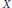$X$ whose support contains the singular locus of 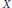$X$ .

Keywords

14B0514E1532S5032S45singularity invarianttopological zeta functionmotivic zeta function

Information

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 53 , Issue 4 , 01 August 2001 , pp. 834 - 865
Copyright
Copyright © Canadian Mathematical Society 2001

References

[AKMW] Abramovich, D., Karu, K., Matsuki, K. and Włodarczyk, J., Torification and factorization of birational maps. Math.AG/9904135, 1999.Google Scholar
[B1] Batyrev, V., Birational Calabi-Yau n-folds have equal Betti numbers. In: New trends in algebraic geometry (Warwick, 1996), London Math. Soc. Lecture Note Ser. 264(eds. Hulek, K. et al.), Cambridge University Press, 1999, 1–11.Google Scholar
[B2] Batyrev, V., Stringy Hodge numbers of varieties with Gorenstein canonical singularities. In: Integrable Systems and Algebraic Geometry (Kobe/Kyoto, 1997), World Sci. Publishing, 1998, 1–32.Google Scholar
[B3] Batyrev, V., Non-Archimedian integrals and stringy Euler numbers of log terminal pairs. J. Eur. Math. Soc. 1(1999), 5–33.Google Scholar
[BLR] Bosch, S., Lütkebohmert, W. and Raynaud, M., Néron Models. In: Ergeb. Math. Grenzgeb. (3) 21, Springer Verlag, Berlin, 1990.Google Scholar
[C] Craw, A., An introduction to motivic integration. Math.AG/9911179, 1999.Google Scholar
[D1] Denef, J., On the degree of Igusa's local zeta function. Amer. J. Math. 109(1987), 991–1008.Google Scholar
[D2] Denef, J., Report on Igusa's local zeta function. Séminaire Bourbaki 741, Astérisque 201–203(1991), 359–386.Google Scholar
[DL1] Denef, J. and Loeser, F., Caractéristiques d’Euler-Poincaré, fonctions zêta locales, et modifications analytiques. J. Amer. Math. Soc. 5(1992), 705–720.Google Scholar
[DL2] Denef, J. and Loeser, F., Motivic Igusa zeta functions. J. Algebraic Geom. 7(1998), 505–537.Google Scholar
[DL3] Denef, J. and Loeser, F., Germs of arcs on singular algebraic varieties and motivic integration. Invent. Math. 135(1999), 201–232.Google Scholar
[DL4] Denef, J. and Loeser, F., Motivic integration, quotient singularities and the McKay correspondence. Compositio Math., to appear.Google Scholar
[Hiro] Hironaka, H., Resolution of singularities of an algebraic variety over a field of characteristic zero. Ann. Math. 79(1964), 109–326.Google Scholar
[Hirz] Hirzebruch, F., Topological methods in algebraic geometry. Springer Verlag, 1966.Google Scholar
[I] Igusa, J., Complex powers and asymptotic expansions I. J. Reine Angew. Math. 268/269(1974), 110–130; II, ibid. 278/279(1975), 307–321.Google Scholar
[KM] Kollár, J. and Mori, S., Birational geometry of algebraic varieties. Cambridge Tracts in Mathematics 134, Cambridge University Press, 1998.Google Scholar
[KMM] Kawamata, Y., Matsuda, K. and Matsuki, K., Introduction to the Minimal Model Program. In: Algebraic geometry (Sendai, 1985), Adv. Stud. Pure Math. 10(1987), 283–360.Google Scholar
[Kol] Kollár, J. et al., Flips and abundance for algebraic threefolds. Seminar (Salt Lake City, 1991), Astérisque 211, 1992.Google Scholar
[Kon] Kontsevich, M., Lecture at Orsay, December 7, 1995.Google Scholar
[L] Loeser, F., Fonctions d’Igusa p-adiques et polynômes de Bernstein. Amer. J. Math. 110(1988), 1–22.Google Scholar
[M] Mumford, D., The topology of normal singularities of an algebraic surface and a criterion for simplicity. Inst. Hautes Études Sci. Publ. Math. 9(1961), 5–22.Google Scholar
[S] Szabó, E., Divisorial log terminal singularities. J. Math. Sci. Univ. Tokyo 1(1994), 631–639.Google Scholar
[V1] Veys, W., Determination of the poles of the topological zeta function for curves. Manuscripta Math. 87(1995), 435–448.Google Scholar
[V2] Veys, W., Zeta functions for curves and log canonical models. Proc. London Math. Soc. 74(1997), 360–378.Google Scholar
[V3] Veys, W., The topological zeta function associated to a function on a normal surface germ. Topology 38(1999), 439–456.Google Scholar
[Wa] Wang, C.-L., On the topology of birational minimal models. J. Differential Geom. 50(1998), 129–146.Google Scholar
[Wł] Włodarczyk, J., Combinatorial structures on toroidal varieties and a proof of the weak factorization theorem. Math.AG/9904076, 1999.Google Scholar