No CrossRef data available.
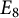 $E_8$
$E_8$Published online by Cambridge University Press: 10 September 2021
We show that the Tits index 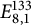 $E_{8,1}^{133}$ cannot be obtained by means of the Tits construction over a field with no odd degree extensions. The proof uses a general method coming from the theory of symmetric spaces. We construct two cohomological invariants, in degrees
$E_{8,1}^{133}$ cannot be obtained by means of the Tits construction over a field with no odd degree extensions. The proof uses a general method coming from the theory of symmetric spaces. We construct two cohomological invariants, in degrees 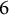 $6$ and
$6$ and  $8$, of the Tits construction and the more symmetric Allison–Faulkner construction of Lie algebras of type
$8$, of the Tits construction and the more symmetric Allison–Faulkner construction of Lie algebras of type 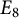 $E_8$ and show that these invariants can be used to detect the isotropy rank.
$E_8$ and show that these invariants can be used to detect the isotropy rank.
The first author was supported by RFBR grant 19-01-00513. The second author was supported by FWO project G004018N.