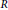Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Dobbs, David E.
2020.
A minimal ring extension of a large finite local prime ring is probably ramified.
Journal of Algebra and Its Applications,
Vol. 19,
Issue. 01,
p.
2050015.
Lei, Antonio
and
Poulin, Antoine
2020.
On Certain Probabilistic Properties of Polynomials over the Ring of p-adic Integers.
The American Mathematical Monthly,
Vol. 127,
Issue. 6,
p.
519.