Published online by Cambridge University Press: 24 October 2019
This paper investigates the computational complexity of deciding if a given finite idempotent algebra has a ternary term operation  $m$ that satisfies the minority equations
$m$ that satisfies the minority equations 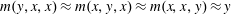 $m(y,x,x)\approx m(x,y,x)\approx m(x,x,y)\approx y$. We show that a common polynomial-time approach to testing for this type of condition will not work in this case and that this decision problem lies in the class NP.
$m(y,x,x)\approx m(x,y,x)\approx m(x,x,y)\approx y$. We show that a common polynomial-time approach to testing for this type of condition will not work in this case and that this decision problem lies in the class NP.
Author A. K. was supported by Charles University grants PRIMUS/SCI/12 and UNCE/SCI/022; J. O. was supported by the European Research Council (Grant Agreement no. 681988, CSP-Infinity) and the UK EPSRC (Grant EP/R034516/1); M. V. was supported by the Natural Sciences and Engineering Council of Canada; D. Z. was supported by the Russian Foundation for Basic Research (grant 19-01-00200).