Hostname: page-component-76fb5796d-25wd4 Total loading time: 0 Render date: 2024-04-26T07:55:23.363Z Has data issue: false hasContentIssue false
  • English
  • Français

Integral mean estimates for univalent and locally univalent harmonic mappings

Part of: Geometric function theory Two-dimensional theory Spaces and algebras of analytic functions

Published online by Cambridge University Press:  15 January 2024

Suman Das Open the ORCID record for Suman Das [Opens in a new window]  and
Anbareeswaran Sairam Kaliraj Open the ORCID record for Anbareeswaran Sairam Kaliraj [Opens in a new window]
Suman Das*
Affiliation:
Department of Mathematics, Indian Institute of Technology Ropar, Rupnagar, Punjab 140001, India, e-mail: sairam@iitrpr.ac.in
Anbareeswaran Sairam Kaliraj
Affiliation:
Department of Mathematics, Indian Institute of Technology Ropar, Rupnagar, Punjab 140001, India, e-mail: sairam@iitrpr.ac.in
*
e-mail: sumandas471@gmail.com
Get access Rights & Permissions [Opens in a new window]

Abstract

We verify a long-standing conjecture on the membership of univalent harmonic mappings in the Hardy space, whenever the functions have a “nice” analytic part. We also produce a coefficient estimate for these functions, which is in a sense best possible. The problem is then explored in a new direction, without the additional hypothesis. Interestingly, our ideas extend to certain classes of locally univalent harmonic mappings. Finally, we prove a Baernstein-type extremal result for the function 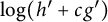$\log (h'+cg')$, when 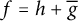$f=h+\overline {g}$ is a close-to-convex harmonic function, and c is a constant. This leads to a sharp coefficient inequality for these functions.

Keywords

Integral meansunivalent harmonic functionsgrowth problemsHardy spaceBaernstein-type inequalities

MSC classification

Primary: 31A05: Harmonic, subharmonic, superharmonic functions 30C45: Special classes of univalent and multivalent functions (starlike, convex, bounded rotation, etc.)
Secondary: 30H10: Hardy spaces
Type
Article
Information
Canadian Mathematical Bulletin , First View , pp. 1 - 15
Check for updates
Copyright
© The Author(s), 2024. Published by Cambridge University Press on behalf of Canadian Mathematical Society

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

The second author was partly supported by the Core Research Grant (CRG/2022/008920) from the Science and Engineering Research Board (SERB), India.

References

Abu-Muhanna, Y. and Lyzzaik, A., The boundary behaviour of harmonic univalent maps . Pacific J. Math. 141(1990), no. 1, 1–20.CrossRefGoogle Scholar
Baernstein, A., Integral means, univalent functions and circular symmetrization . Acta Math. 133(1974), 139–169.CrossRefGoogle Scholar
Baernstein, A., Some sharp inequalities for conjugate functions . Indiana Univ. Math. J. 27(1978), 833–852.CrossRefGoogle Scholar
Brown, J. E., Derivatives of close-to-convex functions, integral means and bounded mean oscillation . Math. Z. 178(1981), 353–358.CrossRefGoogle Scholar
Bshouty, D. and Hengartner, W., Univalent harmonic mappings in the plane . Ann. Univ. Mariae Curie-Skłodowska Sect. A 48(1994), 12–42.Google Scholar
Clunie, J. and Sheil-Small, T., Harmonic univalent functions . Ann. Acad. Sci. Fenn. Ser. A I Math. 9(1984), 3–25.CrossRefGoogle Scholar
Das, S. and Sairam Kaliraj, A., Growth of harmonic mappings and Baernstein type inequalities . Potential Anal. (2023), 17 pp. https://doi.org/10.1007/s11118-023-10081-w Google Scholar
de Branges, L., A proof of the Bieberbach conjecture . Acta Math. 154(1985), 137–152.CrossRefGoogle Scholar
Duren, P. L., Theory of Hp spaces, Pure and Applied Mathematics, 38, Academic Press, New York, 1970.Google Scholar
Duren, P. L., Harmonic mappings in the plane, Cambridge Tracts in Mathematics, 156, Cambridge University Press, Cambridge, 2004.CrossRefGoogle Scholar
Duren, P. L. and Leung, Y. J., Logarithmic coefficients of univalent functions . J. Analyse Math. 36(1979), 36–43.CrossRefGoogle Scholar
Girela, D., Integral means and BMOA-norms of logarithms of univalent functions . J. Lond. Math. Soc. 33(1986), no. 2, 117–132.CrossRefGoogle Scholar
Girela, D., Integral means, bounded mean oscillation, and Gelfer functions . Proc. Amer. Math. Soc. 113(1991), 365–370.Google Scholar
Koosis, P., Introduction to Hp spaces, 2nd ed., Cambridge Tracts in Mathematics, 115, Cambridge University Press, Cambridge, 1998.Google Scholar
Leung, Y. J., Integral means of the derivatives of some univalent functions . Bull. Lond. Math. Soc. 11(1979), 289–294.CrossRefGoogle Scholar
Nowak, M., Some inequalities for BMOA functions . Complex Variables Theory Appl. 16(1991), 81–86.Google Scholar
Nowak, M., Integral means of univalent harmonic maps . Ann. Univ. Mariae Curie-Skłodowska Sect. A 50(1996), 155–162.Google Scholar
Pavlović, M., Introduction to function spaces on the disk, Biblioteka Posebna Izdanja, 20, Matematicki Institut SANU, Belgrade, 2004.Google Scholar
Pommerenke, C., Univalent functions, Vandenhoeck & Ruprecht, Göttingen, 1975.Google Scholar
Ponnusamy, S., Qiao, J., and Wang, X., Uniformly locally univalent harmonic mappings . Proc. Indian Acad. Sci. Math. Sci. 128(2018), Article no. 32, 14 pp.CrossRefGoogle Scholar
Sheil-Small, T., Constants for planar harmonic mappings . J. Lond. Math. Soc. 42(1990), no. 2, 237–248.CrossRefGoogle Scholar
Spencer, D. C., On finitely mean valent functions . Proc. Lond. Math. Soc. 47(1941), no. 2, 201–211.Google Scholar
Wang, X.-T., Liang, X.-Q., and Zhang, Y.-L., Precise coefficient estimates for close-to-convex harmonic univalent mappings . J. Math. Anal. Appl. 263(2001), 501–509.CrossRefGoogle Scholar