No CrossRef data available.
Article contents
Linear fractional self-maps of the unit ball
Published online by Cambridge University Press: 15 November 2023
Abstract
Determining the range of complex maps plays a fundamental role in the study of several complex variables and operator theory. In particular, one is often interested in determining when a given holomorphic function is a self-map of the unit ball. In this paper, we discuss a class of maps in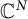 
$\mathbb {C}^N$ that generalize linear fractional maps. We then proceed to determine precisely when such a map is a self-map of the unit ball. In particular, we take a novel approach, obtaining numerous new results about this class of maps along the way.
MSC classification
Primary:
32A10: Holomorphic functions
Information
- Type
- Article
- Information
- Copyright
- © The Author(s), 2023. Published by Cambridge University Press on behalf of The Canadian Mathematical Society
References
Ahn, H., Byun, J., and Park, J.-D.,
Automorphisms of the Hartogs type domains over classical symmetric domains
. Internat. J. Math. 23(2012), 1250098.CrossRefGoogle Scholar
Bisi, C. and Bracci, F.,
Linear fractional maps of the unit ball: A geometric study
. Adv. Math. 167(2002), no. 2, 265–287.CrossRefGoogle Scholar
Cowen, C. and MacCluer, B.,
Linear fractional maps of the ball and Theiry composition operators
. Acta Sci. Math. (Szeged) 66(2000), 351–376.Google Scholar
Humphreys, J., Linear algebraic groups, Graduate Texts in Mathematics, Springer, New York, 1981.Google Scholar
Hinkkanen, A.,
Schur products of certain polynomials, Lipa’s Legacy
. Contemp. Math. 211(1998), 285–295.CrossRefGoogle Scholar
MacCluer, B.,
Iterates of holomorphic self-maps of the unit ball in
${\mathbb{C}}^N$
. Michigan Math. J. 30(1983), no. 1, 97–106.CrossRefGoogle Scholar
${\mathbb{C}}^N$
. Michigan Math. J. 30(1983), no. 1, 97–106.CrossRefGoogle ScholarMartín, M., Composition operators with linear fractional symbols and their adjoints, First Advanced Course in Operator Theory and Complex Analysis, University of Seville, Seville, 2004.Google Scholar
Press, W., Flannery, B., Teukolsky, S., and Vetterling, W., Numerical recipes in Fortran 77: The art of scientific computing. 2nd ed., Cambridge University Press, Cambridge, 1992.Google Scholar
Richman, A.,
The range of linear fractional maps on the unit ball
. Proc. Amer. Math. Soc. 131(2003), 889–895.CrossRefGoogle Scholar
Rudin, W., Function theory in polydiscs, Mathematics Lecture Note Series, 41, W.A. Benjamin, New York, 1969.Google Scholar
Rudin, W., Function theory in the unit ball of
${\mathbb{C}}^n$
, Grundlehren der Mathematischen Wissenschaften [Fundamental Principles of Mathematical Science], 241, Springer, New York, 1980.CrossRefGoogle Scholar
${\mathbb{C}}^n$
, Grundlehren der Mathematischen Wissenschaften [Fundamental Principles of Mathematical Science], 241, Springer, New York, 1980.CrossRefGoogle Scholar