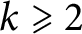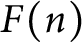Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Das, Sourabhashis
Elma, Ertan
Kuo, Wentang
and
Liu, Yu-Ru
2023.
On the number of irreducible factors with a given multiplicity in function fields.
Finite Fields and Their Applications,
Vol. 92,
Issue. ,
p.
102281.
Elma, Ertan
and
Martin, Greg
2024.
Distribution of the number of prime factors with a given multiplicity.
Canadian Mathematical Bulletin,
Vol. 67,
Issue. 4,
p.
1107.
Das, Sourabhashis
Kuo, Wentang
and
Liu, Yu-Ru
2025.
Distribution of ω(n) over h-free and h-full numbers.
International Journal of Number Theory,
Vol. 21,
Issue. 03,
p.
715.
Das, Sourabhashis
2025.
On limiting distributions of arithmetic functions.
The Ramanujan Journal,
Vol. 68,
Issue. 2,
Wang, Biao
Wei, Zhining
Yan, Pan
and
Yi, Shaoyun
2025.
Generalizations of the Erdős–Kac Theorem and the Prime Number Theorem.
Communications in Mathematics and Statistics,
Vol. 13,
Issue. 5,
p.
1177.
Das, Sourabhashis
Kuo, Wentang
and
Liu, Yu-Ru
2025.
On the number of prime factors with a given multiplicity over h-free and h-full numbers.
Journal of Number Theory,
Vol. 267,
Issue. ,
p.
176.