Published online by Cambridge University Press: 23 August 2021
Fix a poset Q on  $\{x_1,\ldots ,x_n\}$
. A Q-Borel monomial ideal
$\{x_1,\ldots ,x_n\}$
. A Q-Borel monomial ideal 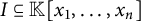 $I \subseteq \mathbb {K}[x_1,\ldots ,x_n]$
is a monomial ideal whose monomials are closed under the Borel-like moves induced by Q. A monomial ideal I is a principal Q-Borel ideal, denoted
$I \subseteq \mathbb {K}[x_1,\ldots ,x_n]$
is a monomial ideal whose monomials are closed under the Borel-like moves induced by Q. A monomial ideal I is a principal Q-Borel ideal, denoted 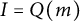 $I=Q(m)$
, if there is a monomial m such that all the minimal generators of I can be obtained via Q-Borel moves from m. In this paper we study powers of principal Q-Borel ideals. Among our results, we show that all powers of
$I=Q(m)$
, if there is a monomial m such that all the minimal generators of I can be obtained via Q-Borel moves from m. In this paper we study powers of principal Q-Borel ideals. Among our results, we show that all powers of 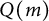 $Q(m)$
agree with their symbolic powers, and that the ideal
$Q(m)$
agree with their symbolic powers, and that the ideal 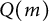 $Q(m)$
satisfies the persistence property for associated primes. We also compute the analytic spread of
$Q(m)$
satisfies the persistence property for associated primes. We also compute the analytic spread of 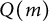 $Q(m)$
in terms of the poset Q.
$Q(m)$
in terms of the poset Q.
Camps is supported by Conacyt. Sarmiento’s research is supported by SNI-Conacyt. Camps and Sarmiento are supported by PIFI IPN 20201016. Van Tuyl’s research is supported by NSERC Discovery Grant 2019-05412.