Hostname: page-component-586b7cd67f-r5fsc Total loading time: 0 Render date: 2024-11-22T23:58:54.432Z Has data issue: false hasContentIssue false
  • English
  • Français

Admissibility of Local Systems for some Classes of Line Arrangements

Published online by Cambridge University Press:  20 November 2018

Nguyen Tat Thang
Nguyen Tat Thang*
Affiliation:
Institute of Mathematics, Vietnam Academy of Science and Technology, 10307 Hanoi, Vietnam and (temporary) Mathematical Institute, Tohoku University, 980-8578 Sendai, Japan e-mail: ntthang@math.ac.vn
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 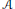$\mathcal{A}$ be a line arrangement in the complex projective plane 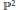${{\mathbb{P}}^{2}}$ and let 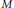$M$ be its complement. A rank one local system 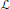$\mathcal{L}$ on 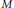$M$ is admissible if, roughly speaking, the cohomology groups 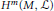${{H}^{m}}\left( M,\,\mathcal{L} \right)$ can be computed directly from the cohomology algebra 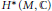${{H}^{*}}\left( M,\,\mathbb{C} \right)$. In this work, we give a sufficient condition for the admissibility of all rank one local systems on 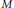$M$. As a result, we obtain some properties of the characteristic variety 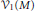${{\mathcal{V}}_{1}}\left( M \right)$ and the Resonance variety 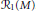${{\mathcal{R}}_{1}}\left( M \right)$.

Keywords

14F9932S2252C3505A1805C4014H50local system, line arrangementcharacteristic varietymultinetresonance variety
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 57 , Issue 3 , 01 September 2014 , pp. 658 - 672
Copyright
Copyright © Canadian Mathematical Society 2014

References

[1] Arapura, D., Geometry of cohomology support loci for local systems. I. J. Algebraic Geom. 6 (1997), no. 3, 563–597.Google Scholar
[2] Beauville, A., Annulation du H1 pour les fibr´es en droites plats. In: Complex algebraic varieties (Bayreuth, 1990), Lecture Notes in Math., 1507, Springer, Berlin, 1992, pp. 1–15.Google Scholar
[3] Choudary, A. D. R., Dimca, A., and Papadima, S., Some analogs of Zariski's theorem on nodal line arrangements. Algebr. Geom. Topol. 5 (2005), 691–711. http://dx.doi.org/10.2140/agt.2005.5.691 Google Scholar
[4] Dimca, A., On admissible rank one local systems. J. Algebra 321 (2009), no. 11, 3145–3157. http://dx.doi.org/10.1016/j.jalgebra.2008.01.039 Google Scholar
[5] Dimca, A. and Maxim, L., Multivariable Alexander invariants of hypersurface complements. Trans. Amer. Math. Soc. 359 (2007), no. 7, 3505–3528. http://dx.doi.org/10.1090/S0002-9947-07-04241-9 Google Scholar
[6] Dimca, A., Papadima, S., and Suciu, A., Topology and geometry of cohomology jump loci. Duke Math. J. 148 (2009), no. 3, 405–457. http://dx.doi.org/10.1215/00127094-2009-030 Google Scholar
[7] Dinh, T., Arrangements de droites et systçmes locaux admissibles. Ph.D. Thesis, Universit´e de Nice, 2009.Google Scholar
[8] Dinh, T., Characteristic varieties for a class of line arrangements. Canad. Math. Bull. 54 (2011), no. 1, 56-67. http://dx.doi.org/10.4153/CMB-2010-092-6 Google Scholar
[9] Eliyahu, M., Garber, D., and Teicher, M., A conjugation-free geometric presentation of fundamental groups of arrangements. Manuscripta Math. 133 (2010), no. 1–2, 247–271. http://dx.doi.org/10.1007/s00229-010-0380-2 Google Scholar
[10] Esnault, H., Schechtman, V., and Viehweg, E., Cohomology of local systems on the complement of hyperplanes. Invent. Math. 109 (1992), 557–561; Erratum, ibid. 112 (1993), 447. http://dx.doi.org/10.1007/BF01232040 Google Scholar
[11] Falk, M., Arrangements and cohomology. Ann. Comb. 1 (1997), no. 2, 135–157. http://dx.doi.org/10.1007/BF02558471 Google Scholar
[12] Falk, M. and Yuzvinsky, S., Multinets, resonance varieties, and pencils of plane curves. Compos. Math. 143 (2007), no. 4, 1069–1088.Google Scholar
[13] Fan, K.-M., Direct product of free groups as the fundamental group of the complement of a union of lines. Michigan Math. J. 44 (1997), no. 2, 283–291. http://dx.doi.org/10.1307/mmj/1029005704 Google Scholar
[14] Green, M. and Lazarsfeld, R., Higher obstructions to deforming cohomology groups of line bundles. J. Amer. Math. Soc. 4 (1991), no. 1, 87–103. http://dx.doi.org/10.1090/S0894-0347-1991-1076513-1 Google Scholar
[15] Jiang, T. and Yau, S. S.-T., Diffeomorphic types of the complements of arrangements of hyperplanes. Compositio Math. 92 (1994), no. 2, 133–155.Google Scholar
[16] Libgober, A. and Yuzvinsky, S., Cohomology of the Orlik-Solomon algebras and local systems. Compositio Math. 121 (2000), no. 3, 337–361. http://dx.doi.org/10.1023/A:1001826010964 Google Scholar
[17] Nazir, S. and Raza, Z., Admissible local systems for a class of line arrangements. Proc. Amer. Math. Soc. 137 (2009), no. 4, 1307–1313. http://dx.doi.org/10.1090/S0002-9939-08-09661-5 Google Scholar
[18] Schechtman, V., Terao, H., and Varchenko, A., Local systems over complements of hyperplanes and the Kac-Kazhdan condition for singular vectors. J. Pure Appl. Alg. 100 (1995), no. 1–3, 93–102. http://dx.doi.org/10.1016/0022-4049(95)00014-N Google Scholar
[19] Simpson, C., Subspaces of moduli spaces of rank one local systems. Ann. Sci. E´ cole Norm. Sup. 26 (1993), no. 3, 361–401.Google Scholar