Hostname: page-component-cd9895bd7-mkpzs Total loading time: 0 Render date: 2024-12-23T10:20:55.779Z Has data issue: false hasContentIssue false
  • English
  • Français

Approximate Fixed Point Sequences of Nonlinear Semigroups in Metric Spaces

Published online by Cambridge University Press:  20 November 2018

M. A. Khamsi
M. A. Khamsi*
Affiliation:
Department of Mathematical Sciences, University of Texas at El Paso, El Paso, TX 79968, USA and Department ofMathematics and Statistics, King Fahd University of Petroleum andMinerals, Dhahran 31261, Saudi Arabia. e-mail: mohamed@utep.edu, e-mail: mkhamsi@kfupm.edu.sa
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this paper, we investigate the common approximate fixed point sequences of nonexpansive semigroups of nonlinear mappings ${{\left\{ {{T}_{t}} \right\}}_{t\ge 0}}$, i.e., a family such that 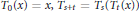${{T}_{0}}\left( x \right)\,=\,x,\,{{T}_{s+t}}\,=\,{{T}_{s}}\left( {{T}_{t}}\left( x \right) \right)$, where the domain is a metric space 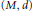$\left( M,\,d \right)$. In particular, we prove that under suitable conditions the common approximate fixed point sequences set is the same as the common approximate fixed point sequences set of two mappings from the family. Then we use the Ishikawa iteration to construct a common approximate fixed point sequence of nonexpansive semigroups of nonlinear mappings.

Keywords

47H0946B2047H1047E10approximate fixed pointfixed pointhyperbolic metric spaceIshikawa iterationsnonexpansive mappingsemigroup of mappingsuniformly convex hyperbolic space
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 58 , Issue 2 , 01 June 2015 , pp. 297 - 305
Copyright
Copyright © Canadian Mathematical Society 2015

References

[1] Belluce, L. P. and Kirk, W. A., Fixed-point theorems for families of contraction mappings. Pacific. J. Math. 18 (1966), 213–217. http://dx.doi.org/10.2140/pjm.1966.18.213 Google Scholar
[2] Belluce, L. P. and Kirk, W. A., Nonexpansive mappings and fixed-points inBanach spaces. Illinois. J. Math. 11 (1967), 474–479.Google Scholar
[3] Browder, E E., Nonexpansive nonlinear operators in a Banach space. Proc. Nat. Acad. Sci. U.S.A. 54 (1965), 1041–1044. http://dx.doi.Org/10.1073/pnas.54.4.1041 Google Scholar
[4] Bruck, R. E., A common fixed point theorem for a commuting family of nonexpansive mappings. Pacific. J. Math. 53 (1974), 59–71. http://dx.doi.Org/10.2140/pjm.1974.53.59 Google Scholar
[5] Busemann, H., Spaces with non-positive curvature. Acta. Math. 80 (1948), 259–310. http://dx.doi.org/10.1007/BF02393651 Google Scholar
[6] Clarkson, J. A., Uniformly convex spaces. Trans. Amer. Math. Soc. 40 (1936), no. 3, 396–414. http://dx.doi.org/10.1090/S0002-9947-1936-1501880-4 Google Scholar
[7] Das, G. and Debata, P., Fixed points of quasi-nonexpansive mappings. Indian J. Pure Appl. Math. 17 (1986), no. 11, 1263–1269.Google Scholar
[8] DeMarr, R. E., Common fixed-points for commuting contraction mappings. Pacific. J. Math. 13 (1963), 1139–1141. http://dx.doi.org/10.2140/pjm.1963.13.1139 Google Scholar
[9] Fukhar-ud-din, H. and Khamsi, M. A., Approximating common fixed points in hyperbolic spaces. Fixed Point Theory Appl., to appear.Google Scholar
[10] Goebel, K. and Reich, S., Uniform convexity, hyperbolic geometry, and nonexpansive mappings. Monographs and Textbooks in Pure and Applied Mathematics, 83, Marcel Dekker, New York, 1984.Google Scholar
[11] Goebel, K., Sekowski, T., and Stachura, A., Uniform convexity of the hyperbolic metric and fixed points of holomorphic mappings in the Hilbert ball. Nonlinear Anal. 4 (1980), no. 5, 1011–1021. http://dx.doi.Org/10.1016/0362-546X(80)90012-7 Google Scholar
[12] Hussain, N. and Khamsi, M. A., On asymptoticpointwise contractions in metric spaces. Nonlinear Anal. 71 (2009), no. 10,4423^429. http://dx.doi.Org/10.1016/j.na.2009.02.126Google Scholar
[13] Khamsi, M. A. and Khan, A. R., Inequalities in metric spaces with applications. Nonlinear Anal. 74 (2011), no. 12,4036–4045. http://dx.doi.Org/10.1016/j.na.2011.03.034 Google Scholar
[14] Kirk, W. A., An abstract fixed point theorem for nonexpansive mappings. Proc. Amer. Math. Soc. 82 (1981), no. 4, 640–642. http://dx.doi.org/10.1090/S0002-9939-1981-0614894-6 Google Scholar
[15] Kirk, W. A., Fixed point theory for nonexpansive mappings. II. In: Fixed points and nonexpansive mappings (Cincinnati, Ohio, 1982), Contemp. Math. 18, American Mathematical Society, Providence, RI, 1983, pp. 121–140.Google Scholar
[16] Kirk, W. A., A fixed point theorem in CAT(O) spaces and R-trees. Fixed Point Theory Appl. 2004, no. 4, 309–316.Google Scholar
[17] Kirk, W. A. and Xu, H. K., Asymptoticpointwise contractions. Nonlinear Anal. 69 (2008), no. 12, 4706–4712. http://dx.doi.Org/10.1016/j.na.2007.11.023 Google Scholar
[18] Leustean, L., A quadratic rate of asymptotic regularity for CAT(O)-spaces. J. Math. Anal. Appl. 325 (2007), no. 1, 386–399. http://dx.doi.org/10.101 6/j.jmaa.2006.01.081 Google Scholar
[19] Lim, T. C., A fixed point theorem for families ofnonexpansive mappings. Pacific J. Math. 53 (1974), 487–493. http://dx.doi.org/10.2140/pjm.1974.53.487 Google Scholar
[20] Menger, K., Untersuchungen iiber allgemeineMetrik. Math. Ann. 100 (1928), no. 1, 75–163. http://dx.doi.Org/10.1007/BF01448840 Google Scholar
[21] Reich, S. and Shafrir, I., Nonexpansive iterations in hyperbolic spaces. Nonlinear Anal. 15 (1990), no. 6, 537–558. http://dx.doi.Org/10.1016/0362-546X(90)90058-O Google Scholar
[22] Shimizu, T., A convergence theorem to common fixed points of families of nonexpansive mappings in convex metric spaces. In: Nonlinear analysis and convex analysis, Yokohama Publ., Yokohama, 2007, pp. 575–585.Google Scholar
[23] Stewart, I. and Tall, D., Algebraic number theory and Fermat's last theorem, Third éd., A K Peters Ltd, Natick, MA, 2002.Google Scholar