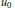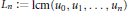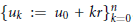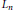Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Hong, Shaofang
and
Qian, Guoyou
2017.
New lower bounds for the least common multiple of polynomial sequences.
Journal of Number Theory,
Vol. 175,
Issue. ,
p.
191.
Qian, Guoyou
2017.
On the sum of reciprocals of least common multiples.
Comptes Rendus. Mathématique,
Vol. 355,
Issue. 11,
p.
1127.
Zhao, Jianrong
Qian, Guoyou
and
Zhao, Wei
2021.
On the sum of reciprocals of least common multiples, II.
Applied Mathematics and Computation,
Vol. 399,
Issue. ,
p.
126003.
Bousla, Sid Ali
2021.
Nontrivial upper bounds for the least common multiple of an arithmetic progression.
Asian-European Journal of Mathematics,
Vol. 14,
Issue. 08,
p.
2150138.
Fang, Jin-Hui
and
Ma, Jie
2022.
The sum of reciprocals of least common multiples.
Periodica Mathematica Hungarica,
Vol. 84,
Issue. 1,
p.
119.
Chiu, Sunben
He, Yuqing
and
Yuan, Pingzhi
2022.
The exact upper bound for the sum of reciprocals of least common multiples.
Applied Mathematics and Computation,
Vol. 416,
Issue. ,
p.
126756.