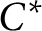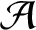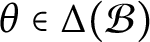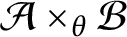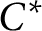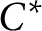Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Amiri, Mitra
and
Rejali, Ali
2024.
$$C^{*}$$-algebra structure on vector valued-Banach algebras.
Monatshefte für Mathematik,
Vol. 203,
Issue. 1,
p.
1.