No CrossRef data available.
Article contents
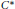${{C}^{*}}$ -Algebras and Factorization Through Diagonal Operators
Published online by Cambridge University Press: 20 November 2018
Abstract
Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.
Let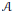 
$\mathcal{A}$ be a 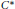${{C}^{*}}$ -algebra and 
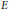$E$ be a Banach space with the Radon-Nikodym property. We prove that if 
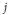$j$ is an embedding of 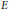$E$ into an injective Banach space then for every absolutely summing operator 
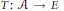$T:\,\mathcal{A}\,\to \,E$ , the composition 
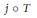$j\,\circ \,T$ factors through a diagonal operator from 
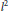${{l}^{2}}$ into 
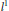${{l}^{1}}$ . In particular, 
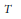$T$ factors through a Banach space with the Schur property. Similarly, we prove that for 
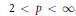$2\,<\,p\,<\,\infty $ , any absolutely summing operator from 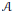$\mathcal{A}$ into 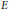$E$ factors through a diagonal operator from 
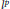${{l}^{p}}$ into 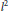${{l}^{2}}$ .
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 2004
References
[1]
Diestel, J., Sequences and series in Banach spaces. Graduate Texts in Mathematics, 92, Springer-Verlag, New York, 1984.Google Scholar
[2]
Diestel, J., Jarchow, H., and Tonge, A., Absolutely summing operators, Cambridge University Press, Cambridge, 1995.Google Scholar
[3]
Diestel, J. and Uhl, J. J. Jr., Vector measures. Math. Surveys, 15, American Mathematical Society, Providence, R.I., 1977.Google Scholar
[4]
Kadison, K. V. and Ringrose, J. R., Fundamentals of the theory of operator algebras. Vol. I: Elementary theory. Academic Press, New York, 1983.Google Scholar
[5]
Kadison, K. V. and Ringrose, J. R., Fundamentals of the theory of operator algebras. Vol. II: Advanced theory. Academic Press, New York, 1986.Google Scholar
[7]
Randrianantoanina, N., Factorization of operators on C*-algebras. Studia Math. 128 (1998), 273–285.Google Scholar
[8]
Randrianantoanina, N., Absolutely summing operators on non commutative C*-algebras and applications. Houston J. Math. 25 (1999), 745–755.Google Scholar
[9]
Randrianantoanina, N., Compact range property and operators on C*-algebras. Proc. Amer. Math. Soc. 129 (2001), 865–871.Google Scholar
[10]
Saphar, P., Applications p décomposantes et p absolument sommantes. Israel J. Math. 11 (1972), 164–179.Google Scholar
[12]
Upmeier, H., Symmetric Banach manifolds and Jordan C*-algebras. Notas de Matemática [Mathematical Notes], 96. North-Holland, Amsterdam, 1985.Google Scholar
You have
Access