Hostname: page-component-cb9f654ff-d5ftd Total loading time: 0 Render date: 2025-08-07T17:05:03.729Z Has data issue: false hasContentIssue false
  • English
  • Français

Carmichael Meets Chebotarev

Published online by Cambridge University Press:  20 November 2018

William D. Banks ,
Ahmet M. Güloğlu  and
Aaron M. Yeager
William D. Banks
Affiliation:
Department of Mathematics, University of Missouri, Columbia, MO 65211 USA e-mail: bankswd@missouri.edu
Ahmet M. Güloğlu
Affiliation:
Department of Mathematics, Bilkent University, 06800 Bilkent, Ankara, Turkey e-mail: guloglua@fen.bilkent.edu.tr
Aaron M. Yeager
Affiliation:
Department of Mathematics, University of Missouri, Columbia, MO 65211, USA e-mail: amydm6@mail.missouri.edu
Rights & Permissions [Opens in a new window]

Abstract.

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

For any finite Galois extension $K$ of 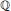$\mathbb{Q}$ and any conjugacy class 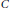$C$ in 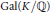$\text{Gal}\left( {K}/{\mathbb{Q}}\; \right)$ , we show that there exist infinitely many Carmichael numbers composed solely of primes for which the associated class of Frobenius automorphisms is 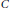$C$ . This result implies that for every natural number $n$ there are infinitely many Carmichael numbers of the form 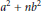${{a}^{2}}\,+\,n{{b}^{2}}$ with 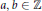$a,\,b\,\in \,\mathbb{Z}$ .

Keywords

11N2511R45Carmichael numbersChebotarev density theorem

Information

Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 56 , Issue 4 , 01 December 2013 , pp. 695 - 708
Copyright
Copyright © Canadian Mathematical Society 2013

References

[1] Alford, W. R., Granville, A., and Pomerance, C., There are infinitely many Carmichael numbers. Ann. of Math. (2) 139 (1994), no. 3, 703–722. http://dx.doi.org/10.2307/2118576 Google Scholar
[2] Banks, W. D., Carmichael numbers with a square totient. Canad. Math. Bull. 52 (2009), no. 1, 3–8. http://dx.doi.org/10.4153/CMB-2009-001-7 Google Scholar
[3] Banks, W. D. and Pomerance, C., On Carmichael numbers in arithmetic progressions. J. Austral. Math. Soc. 88 (2010), no. 3, 313–321. http://dx.doi.org/10.1017/S1446788710000169 Google Scholar
[4] Cox, D. A., Primes of the form x2 + ny2. Fermat, class field theory and complex multiplication. John Wiley & Sons, Inc., New York, 1989.Google Scholar
[5] Dummit, D. S. and Foote, R. M., Abstract algebra. Third ed. John Wiley & Sons, Inc., Hoboken, NJ, 2004.Google Scholar
[6] Ekstrom, A., Pomerance, C., and Thakur, D. S., Infinitude of elliptic Carmichael numbers. J. Austral. Math. Soc. 92 (2012), 45–60. http://dx.doi.org/10.1017/S1446788712000080 Google Scholar
[7] Friedlander, J. B., Shifted primes without large prime factors. In: Number theory and applications (Banff, AB, 1988), NATO Adv. Sci. Inst. Ser. C Math. Phys. Sci., 265, Kluwer Acad. Publ., Dordrecht, 1989, pp. 393–401.Google Scholar
[8] Grantham, J., There are infinitely many Perrin pseudoprimes. J. Number Theory 130 (2010), no. 5, 1117–1128. http://dx.doi.org/10.1016/j.jnt.2009.11.008 Google Scholar
[9] Janusz, G. J., Algebraic number fields. Pure and Applied Mathematics, 55, Academic Press, New York-London, 1973.Google Scholar
[10] Lagarias, J. C. and Odlyzko, A. M., Effective versions of the Chebotarev density theorem. In: Algebraic number fields: L-functions and Galois properties (Proc. Sympos., Univ. Durham, Durham, 1975), Academic Press, London, 1977, pp. 409–464.Google Scholar
[11] Matomäki, K., Carmichael numbers in arithmetic progressions. J. Austral. Math. Soc., to appear.Google Scholar
[12] Montgomery, H.L. and Vaughan, R. C., The large sieve. Mathematika 20 (1973), 119–134. http://dx.doi.org/10.1112/S0025579300004708 Google Scholar
[13] Neukirch, J., Algebraic number theory. Grundlehren der MathematischenWissenschaften, 322, Springer-Verlag, Berlin, 1999.Google Scholar
[14] Rosser, J. B. and Schoenfeld, L., Approximate formulas for some functions of prime numbers. Illinois J. Math. 6 (1962), 64–94.Google Scholar
[15] Washington, L. C., Introduction to cyclotomic fields. Second ed., Graduate Texts in Mathematics, 83, Springer-Verlag, New York, 1997.Google Scholar
[16] Weiss, A., The least prime ideal. J. Reine Angew. Math. 338 (1983), 56–94.Google Scholar