No CrossRef data available.
Article contents
Character Sums with Division Polynomials
Published online by Cambridge University Press: 20 November 2018
Abstract
Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.
We obtain nontrivial estimates of quadratic character sums of division polynomials 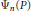 ${{\text{ }\!\!\psi\!\!\text{ }}_{n}}\left( P \right)$ ,
${{\text{ }\!\!\psi\!\!\text{ }}_{n}}\left( P \right)$ , 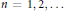 $n\,=\,1,\,2,\,\ldots $ , evaluated at a given point
$n\,=\,1,\,2,\,\ldots $ , evaluated at a given point  $P$ on an elliptic curve over a finite field of
$P$ on an elliptic curve over a finite field of  $q$ elements. Our bounds are nontrivial if the order of
$q$ elements. Our bounds are nontrivial if the order of  $P$ is at least
$P$ is at least 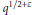 ${{q}^{{}^{1}/{}_{2+\varepsilon }}}$ for some fixed
${{q}^{{}^{1}/{}_{2+\varepsilon }}}$ for some fixed 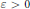 $\varepsilon \,>\,0$ . This work is motivated by an open question about statistical indistinguishability of some cryptographically relevant sequences that was recently brought up by K. Lauter and the second author.
$\varepsilon \,>\,0$ . This work is motivated by an open question about statistical indistinguishability of some cryptographically relevant sequences that was recently brought up by K. Lauter and the second author.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 2012
References
[1] Chen, Z., Elliptic curve analogue of Legendre sequences. Monatsh. Math.
154(2008), no. 1, 1–10. http://dx.doi.org/10.1007/s00605-008-0520-x
Google Scholar
[2] Everest, G., van der Poorten, A. J., Shparlinski, I. E., and Ward, T., Recurrence Sequences. Mathematical Surveys and Monographs 104. American Mathematical Society, Providence, RI, 2003.Google Scholar
[3] Iwaniec, H. and Kowalski, E., Analytic Number Theory. American Mathematical Society Colloquium Publications 53. American Mathematical Society, Providence, RI, 2004.Google Scholar
[4] Kohel, D. R. and Shparlinski, I. E., On exponential sums and group generators for elliptic curves over finite fields. Lecture Notes in Comput. Sci. 1838, Springer, Berlin, 2000, pp. 395–404.Google Scholar
[5] Lauter, K. E. and Stange, K. E., The elliptic curve discrete logarithm problem and equivalent hard problems for elliptic divisibility sequences. Lecture Notes in Comput. Sci. 5381, Springer-Verlag, Berlin, 2009, pp. 309–327.Google Scholar
[6] Perret, M., Multiplicative character sums and Kummer coverings. Acta Arith.
59(1991), no. 3, 279–290.Google Scholar
[7] Russell, A. C. and Shparlinski, I. E., Classical and quantum function reconstruction via character evaluation.
J. Complexity
20(2004), no. 2-3, 404–422. http://dx.doi.org/10.1016/j.jco.2003.08.019
Google Scholar
[8] Shparlinski, I. E., Distribution of nonresidues and primitive roots in recurrent sequences. Mat. Zametki
24(1978), no. 5, 603–613, 733, (in Russian).Google Scholar
[9] Silverman, J. H., The Arithmetic of Elliptic Curves.
Second edition. Graduate Texts in Mathematics 106. Springer, Dordrecht, 2009.Google Scholar
[10] Silverman, J. H., p-adic properties of division polynomials and elliptic divisibility sequences. Math. Ann.
332(2005), no. 2, 443–471. http://dx.doi.org/10.1007/s00208-004-0608-0
Google Scholar
[11] Swart, C., Elliptic Curves and Related Sequences. Ph.D. thesis, Royal Holloway and Bedford New College, University of London, 2003.Google Scholar
[12] Ward, M., Memoir on elliptic divisibility sequences. Amer. J. Math.
70(1948), 31–74. http://dx.doi.org/10.2307/2371930
Google Scholar

