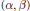Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Pişcoran, Laurian-Ioan
and
Mishra, Vishnu Narayan
2017.
S-curvature for a new class of $$(\alpha , \beta )$$ ( α , β ) -metrics.
Revista de la Real Academia de Ciencias Exactas, Físicas y Naturales. Serie A. Matemáticas,
Vol. 111,
Issue. 4,
p.
1187.
Li, Ying
and
Mo, Xiaohuan
2019.
On dually flat square metrics.
Differential Geometry and its Applications,
Vol. 62,
Issue. ,
p.
60.
张, 娜
2022.
Cartan Torsion of Minkowskian Product Finsler Manifold.
Pure Mathematics,
Vol. 12,
Issue. 05,
p.
826.