Hostname: page-component-8448b6f56d-jr42d Total loading time: 0 Render date: 2024-04-23T22:39:34.440Z Has data issue: false hasContentIssue false
  • English
  • Français

A Classification of Three-dimensional Real Hypersurfaces in Non-flat Complex Space Forms in Terms of their Generalized Tanaka–Webster Lie Derivative

Published online by Cambridge University Press:  20 November 2018

George Kaimakamis ,
Konstantina Panagiotidou  and
Juan de Dios Perez
George Kaimakamis
Affiliation:
Faculty of Mathematics and Engineering Sciences, Hellenic Military Academy, Vari, Attiki, Greece e-mail: gmiamis@gmail.com e-mail: konpanagiotidou@gmail.com
Konstantina Panagiotidou
Affiliation:
Faculty of Mathematics and Engineering Sciences, Hellenic Military Academy, Vari, Attiki, Greece e-mail: gmiamis@gmail.com e-mail: konpanagiotidou@gmail.com
Juan de Dios Perez
Affiliation:
Departmento de Geometria y Topologia, Universidad de Granada, 18071, Granada Spain e-mail: jdperez@ugr.es
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

On a real hypersurface 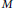$M$ in a non-flat complex space form there exist the Levi–Civita and the $k$-th generalized Tanaka–Webster connections. The aim of this paper is to study three dimensional real hypersurfaces in non-flat complex space forms, whose Lie derivative of the structure Jacobi operatorwith respect to the Levi–Civita connection coincides with the Lie derivative of it with respect to the $k$-th generalized Tanaka-Webster connection. The Lie derivatives are considered in direction of the structure vector field and in direction of any vector field orthogonal to the structure vector field.

Keywords

53C1553B25k-th generalized Tanaka–Webster connectionnon-flat complex space formreal hypersurfaceLie derivativestructure Jacobi operator
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 59 , Issue 4 , 01 December 2016 , pp. 813 - 823
Copyright
Copyright © Canadian Mathematical Society 2016

References

[1] Berndt, J., Real hypersurfaces with constant principal curvatures in complex hyperbolic space. J. Reine Angew. Math. 395(1989), 132–141. http://dx.doi.Org/10.1515/crll.1989.395.132 Google Scholar
[2] Cho, J. T., CR structures on real hypersurfaces of a complex space form. Publ. Math. Debrecen 54(1999), no. 3-4, 473–487.Google Scholar
[3] Cho, J. T., Pseudo-Einstein CR-structures on real hypersurfaces in a complex space form. Hokkaido Math. J. 37(2008), no. 1, 1–17. http://dx.doi.Org/10.14492/hokmj71253539581 Google Scholar
[4] Ivey, T. A. and P. Ryan, J., The structure Jacobi operator for real hypersurfaces in CP2 and CH2. Results Math. 56(2009), no. 1-4, 473–488. http://dx.doi.Org/10.1007/s00025-009-0380-2 Google Scholar
[5] Ki, U.-H. and Suh, Y. J., On real hypersurfaces of a complex space form. Math. J. Okayama Univ. 32(1990), 207–221.Google Scholar
[6] Kimura, M., Real hypersurfaces and complex submanifolds in complex protective space. Trans. Amer. Math. Soc. 296(1986), no. 1,137-149. http://dx.doi.Org/10.1090/S0002-9947-1986-0837803-2 Google Scholar
[7] Maeda, Y., On real hypersurfaces of a complex protective space. J. Math. Soc. Japan 28(1976), no. 3, 529–540. http://dx.doi.Org/10.2969/jmsj702830529 Google Scholar
[8] Montiel, S., Real hypersurfaces of a complex hyperbolic space. J. Math. Soc. Japan 35(1985), no. 3, 515–535. http://dx.doi.Org/10.2969/jmsj703730515 Google Scholar
[9] Montiel, S. and Romero, A., On some real hypersurfaces of a complex hyperbolic space. Geom. Dedicata 20(1986), no. 2, 245–261. http://dx.doi.Org/10.1007/BF00164402 Google Scholar
[10] Niebergall, R. and Ryan, P. J., Real hypersurfaces in complex space forms. In: Tight and taut submanifolds, Math. Sci. Res. Inst. Publ., 32, Cambridge University Press, Cambridge, 1997, pp. 233–305.Google Scholar
[11] Okumura, M., On some real hypersurfaces of a complex projective space. Trans. Amer. Math. Soc. 212(1975), 355–364. http://dx.doi.Org/10.1090/S0002-9947-1975-0377787-X Google Scholar
[12] Panagiotidou, K. and Xenos, Ph. J., Real hypersurfaces in CP2 and CH2 whose structure Jacobi operator is Lie ID-parallel. Note Mat. 32(2012), no. 2, 89–99.Google Scholar
[13] Takagi, R., On homogeneous real hypersurfaces in a complex projective space. Osaka J. Math. 10(1973), 495–506.Google Scholar
[14] Takagi, R., Real hypersurfaces in complex projective space with constant principal curvatures. J. Math. Soc. Japan 27(1975), 43–53. http://dx.doi.Org/10.2969/jmsj702710043 Google Scholar
[15] Takagi, R., Real hypersurfaces in complex projective space with constant principal curvatures. II. J. Math. Soc. Japan 27(1975), no. 4, 507–516. http://dx.doi.Org/10.2969/jmsj702740507 Google Scholar
[16] Tanaka, N., On non-degenerate real hypersurfaces, graded Lie algebras and Cartan connections. Japan. J. Math. 2(1976), no. 1,131-190.Google Scholar
[17] Tanno, S., Variational problems on contact Riemannian manifolds. Trans. Amer. Math. Soc. 314(1989), 349–379. http://dx.doi.Org/10.1090/S0002-9947-1989-1000553-9 Google Scholar
[18] Webster, S. M., Pseudohermitian structures on a real hypersurface. J. Diff. Geom. 13(1978), no. 1, 25–41.Google Scholar