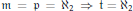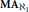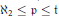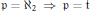Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Halbeisen, Lorenz J.
2012.
Combinatorial Set Theory.
p.
179.
Malliaris, Maryanthe
and
Shelah, Saharon
2013.
General topology meets model theory, on 𝔭 and 𝔱.
Proceedings of the National Academy of Sciences,
Vol. 110,
Issue. 33,
p.
13300.