Hostname: page-component-76c49bb84f-zv2rg Total loading time: 0 Render date: 2025-07-12T02:57:55.971Z Has data issue: false hasContentIssue false
  • English
  • Français

Construction of Generalized Harish-Chandra Modules with Arbitrary Minimal -Type

Published online by Cambridge University Press:  20 November 2018

Ivan Penkov  and
Gregg Zuckerman
Ivan Penkov
Affiliation:
Jacobs University Bremen, Campus Ring 1, D-28759 Bremen, Germany e-mail: i.penkov@ijacobs-university.de
Gregg Zuckerman
Affiliation:
Department of Mathemaics, Yale University, New Haven, CT 06520-8283, U.S.A. e-mail: gregg@math.yale.edu
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 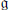$\mathfrak{g}$ be a semisimple complex Lie algebra and 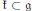$\mathfrak{k}\,\subset \mathfrak{g}$ be any algebraic subalgebra reductive in 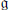$\mathfrak{g}$. For any simple finite dimensional 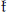$\mathfrak{k}$-module 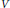$V$, we construct simple 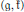$\left( \mathfrak{g},\mathfrak{k} \right)$-modules 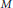$M$ with finite dimensional 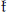$\mathfrak{k}$-isotypic components such that 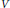$V$ is a 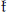$\mathfrak{k}$-submodule of 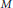$M$ and the Vogan norm of any simple 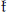$\mathfrak{k}$-submodule 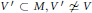$V\prime \subset M,V\prime \ne \,V$, is greater than the Vogan norm of 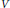$V$. The 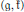$\left( \mathfrak{g},\mathfrak{k} \right)$-modules 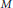$M$ are subquotients of the fundamental series of 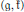$\left( \mathfrak{g},\mathfrak{k} \right)$-modules.

Keywords

17B1017B55

Information

Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 50 , Issue 4 , 01 December 2007 , pp. 603 - 609
Copyright
Copyright © Canadian Mathematical Society 2007

References

[1] Fernando, S., Lie algebra modules with finite-dimensional weight spaces. I. Trans. Amer. Math. Soc. 322(1990), no. 2, 757–781.Google Scholar
[2] Mathieu, O., Classification of irreducible weight modules. Ann. Inst. Fourier (Grenoble) 50(2000), 537–592.Google Scholar
[3] Penkov, I., Serganova, V., and Zuckerman, G., On the existence of (g, k)-modules of finite type. Duke Math. J. 125(2004), no. 2, 329–349.Google Scholar
[4] Penkov, I. and Zuckerman, G., Generalized Harish-Chandra modules: a new direction in the structure theory of representations. Acta Appl. Math. 81(2004), no. 1-3, 311–326.Google Scholar
[5] Penkov, I. and Zuckerman, G., Generalized Harish-Chandra modules with a generic minimal k-type. Asian J. Math. 8 2004, no. 4, 795–811.Google Scholar
[6] Vogan, D., Representations of Real Reductive Lie Groups. Progress in Mathematics 15, Birkhäuser, Boston, 1981.Google Scholar