In 2012, Gubeladze (Adv. Math. 2012) introduced the notion of $k$ -convex-normal polytopes to show that integral polytopes all of whose edges are longer than 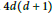$4d(d+1)$ have the integer decomposition property. In the first part of this paper we show that for lattice polytopes there is no diòerence between $k$ - and 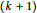$(k+1)$ -convex-normality (for 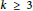$k\ge 3$ ) and improve the bound to 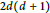$2d(d+1)$ . In the second part we extend the definition to pairs of polytopes. Given two rational polytopes $P$ and 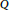$\text{Q}$ , where the normal fan of $P$ is a refinement of the normal fan of 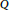$\text{Q}$ , if every edge 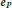${{e}_{P}}$ of $P$ is at least $d$ times as long as the corresponding face (edge or vertex) 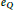${{e}_{\text{Q}}}$ of 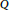$\text{Q}$ , then 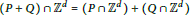$(P+\text{Q})\cap {{\mathbb{Z}}^{d}}=(P\cap {{\mathbb{Z}}^{d}})+(\text{Q}\cap {{\mathbb{Z}}^{d}})$ .