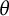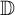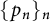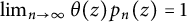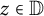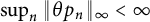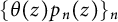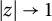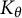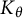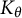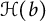1 Background and the main results
1.1 Cyclic singular inner functions
Let X be a topological space consisting of functions which are analytic in the unit disk
![]() $\mathbb {D} = \{ z \in \mathbb {C} : |z| < 1\}$
and which satisfy some customary desirable properties, such as that the evaluation
$\mathbb {D} = \{ z \in \mathbb {C} : |z| < 1\}$
and which satisfy some customary desirable properties, such as that the evaluation
![]() $f \mapsto f(\lambda )$
is a continuous functional on X for each
$f \mapsto f(\lambda )$
is a continuous functional on X for each
![]() $\lambda \in \mathbb {D}$
and that the function
$\lambda \in \mathbb {D}$
and that the function
![]() $z \mapsto zf(z)$
is contained in the space X whenever
$z \mapsto zf(z)$
is contained in the space X whenever
![]() $f \in X$
. A function
$f \in X$
. A function
![]() $g \in X$
is said to be cyclic if there exists a sequence of analytic polynomials
$g \in X$
is said to be cyclic if there exists a sequence of analytic polynomials
![]() $\{p_n\}_n$
for which the polynomial multiples
$\{p_n\}_n$
for which the polynomial multiples
![]() $\{gp_n\}_n$
converge to the constant function
$\{gp_n\}_n$
converge to the constant function
![]() $1$
in the topology of the space.
$1$
in the topology of the space.
The well-known Hardy classes
![]() $H^p$
are among the very few examples of analytic function spaces in which the cyclicity phenomenon is completely understood. The cyclic functions g are of the form
$H^p$
are among the very few examples of analytic function spaces in which the cyclicity phenomenon is completely understood. The cyclic functions g are of the form
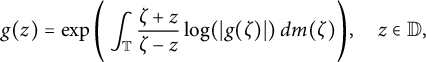 $$ \begin{align} g(z) = \exp\Bigg( \int_{\mathbb{T}} \frac{\zeta + z}{\zeta - z} \log(|g(\zeta)|) \, d\textit{m}(\zeta)\Bigg), \quad z \in \mathbb{D}, \end{align} $$
$$ \begin{align} g(z) = \exp\Bigg( \int_{\mathbb{T}} \frac{\zeta + z}{\zeta - z} \log(|g(\zeta)|) \, d\textit{m}(\zeta)\Bigg), \quad z \in \mathbb{D}, \end{align} $$
where
![]() $d\textit {m}$
is the (normalized) Lebesgue measure of the unit circle
$d\textit {m}$
is the (normalized) Lebesgue measure of the unit circle
![]() $\mathbb {T} = \{ z\in \mathbb {C} : |z| = 1\}$
. Functions as in (1.1) are called outer functions. The inner functions are of the form
$\mathbb {T} = \{ z\in \mathbb {C} : |z| = 1\}$
. Functions as in (1.1) are called outer functions. The inner functions are of the form
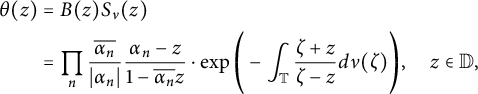 $$ \begin{align} \theta(z) & = B(z) S_\nu(z) \nonumber \\ & = \prod_{n} \frac{\overline{\alpha_n}}{|\alpha_n|}\frac{\alpha_n - z}{1-\overline{\alpha_n}z} \cdot \exp\Bigg( -\int_{\mathbb{T}} \frac{\zeta + z}{\zeta - z} d\nu(\zeta)\Bigg), \quad z \in \mathbb{D}, \end{align} $$
$$ \begin{align} \theta(z) & = B(z) S_\nu(z) \nonumber \\ & = \prod_{n} \frac{\overline{\alpha_n}}{|\alpha_n|}\frac{\alpha_n - z}{1-\overline{\alpha_n}z} \cdot \exp\Bigg( -\int_{\mathbb{T}} \frac{\zeta + z}{\zeta - z} d\nu(\zeta)\Bigg), \quad z \in \mathbb{D}, \end{align} $$
where
![]() $\nu $
is a positive finite singular Borel measure on
$\nu $
is a positive finite singular Borel measure on
![]() $\mathbb {T}$
and
$\mathbb {T}$
and
![]() $\{\alpha _n\}_n$
is a Blaschke sequence. It is clear that if the Blaschke product B on the left is nontrivial, then
$\{\alpha _n\}_n$
is a Blaschke sequence. It is clear that if the Blaschke product B on the left is nontrivial, then
![]() $\theta $
vanishes at points in
$\theta $
vanishes at points in
![]() $\mathbb {D}$
and therefore cannot be cyclic in any reasonable space of analytic functions X. The right factor
$\mathbb {D}$
and therefore cannot be cyclic in any reasonable space of analytic functions X. The right factor
![]() $S_\nu $
is a singular inner function, and it is well known that if a function
$S_\nu $
is a singular inner function, and it is well known that if a function
![]() $g \in H^p$
has a singular inner function as a factor, then g is not cyclic in
$g \in H^p$
has a singular inner function as a factor, then g is not cyclic in
![]() $H^p$
. As a consequence, if
$H^p$
. As a consequence, if
![]() $\{p_n\}_n$
is a sequence of polynomials for which we have
$\{p_n\}_n$
is a sequence of polynomials for which we have
then necessarily the Hardy class norms of the sequence must explode
for finite
![]() $p \geq 1$
, or in case
$p \geq 1$
, or in case
![]() $p = \infty $
,
$p = \infty $
,
When other norms are considered, cyclic singular inner functions might exist, and here the Bergman spaces
![]() $L^p_a(\mathbb {D})$
provide a famous set of examples. The Bergman norms are of the form
$L^p_a(\mathbb {D})$
provide a famous set of examples. The Bergman norms are of the form
where
![]() $dA$
is the normalized area measure of
$dA$
is the normalized area measure of
![]() $\mathbb {D}$
. After a sequence of partial results by multiple authors, Korenblum in [Reference Korenblum12] and Roberts in [Reference Roberts15] independently characterized the cyclic singular inner functions in the Bergman spaces in terms of the vanishing on certain subsets of
$\mathbb {D}$
. After a sequence of partial results by multiple authors, Korenblum in [Reference Korenblum12] and Roberts in [Reference Roberts15] independently characterized the cyclic singular inner functions in the Bergman spaces in terms of the vanishing on certain subsets of
![]() $\mathbb {T}$
of the corresponding singular measure
$\mathbb {T}$
of the corresponding singular measure
![]() $\nu $
appearing in (1.2). A construction of a singular inner function which is cyclic in the classical Bloch space appears in [Reference Anderson, Fernandez and Shields3].
$\nu $
appearing in (1.2). A construction of a singular inner function which is cyclic in the classical Bloch space appears in [Reference Anderson, Fernandez and Shields3].
Recently, Ransford in [Reference Ransford14] noted that singular inner functions exist which decay arbitrarily slowly near the boundary of the disk. As we shall see below, this fact has as a direct consequence the existence of an abundance of spaces of analytic function which admit cyclic singular inner functions. Here is the precise statement of the main result of [Reference Ransford14].
Theorem 1.1 Let
![]() $w:[0,1) \to (0,1)$
be any function satisfying
$w:[0,1) \to (0,1)$
be any function satisfying
![]() $\lim _{r \to 1^-} w(r) = 0$
. Then there exists a singular inner function
$\lim _{r \to 1^-} w(r) = 0$
. Then there exists a singular inner function
![]() $\theta $
for which we have
$\theta $
for which we have
It has been remarked to the present author that, in fact, this theorem appears already in the literature. For instance, Shapiro similarly mentions in [Reference Shapiro17] that a singular inner function always satisfies an estimate of the form
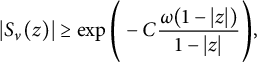 $$ \begin{align} |S_\nu(z)| \geq \exp\Bigg(- C \frac{\omega(1-|z|)}{1-|z|}\Bigg), \end{align} $$
$$ \begin{align} |S_\nu(z)| \geq \exp\Bigg(- C \frac{\omega(1-|z|)}{1-|z|}\Bigg), \end{align} $$
where C is some positive constant, and
![]() $\omega = \omega _\nu $
is the modulus of continuity of the measure
$\omega = \omega _\nu $
is the modulus of continuity of the measure
![]() $\nu $
:
$\nu $
:
The supremum above is taken over arcs I of the circle
![]() $\mathbb {T}$
which are of length h. In [Reference Shapiro18], Shapiro proves that a singular measure
$\mathbb {T}$
which are of length h. In [Reference Shapiro18], Shapiro proves that a singular measure
![]() $\nu $
exists with a modulus of continuity
$\nu $
exists with a modulus of continuity
![]() $\omega _\nu $
for which
$\omega _\nu $
for which
![]() $\omega _\nu (h)/h$
grows to infinity arbitrarily slowly as h decreases to zero, hence proving Theorem 1.1 as a consequence of the estimate (1.4). In fact, such singular measures have been known to exist at least since the work of Hartman and Kershner in [Reference Hartman and Kershner10]. The proof of Ransford in [Reference Ransford14] also involves establishing the existence of such a measure.
$\omega _\nu (h)/h$
grows to infinity arbitrarily slowly as h decreases to zero, hence proving Theorem 1.1 as a consequence of the estimate (1.4). In fact, such singular measures have been known to exist at least since the work of Hartman and Kershner in [Reference Hartman and Kershner10]. The proof of Ransford in [Reference Ransford14] also involves establishing the existence of such a measure.
The following result is the abovementioned consequence of Theorem 1.1 on existence of cyclic singular inner function. The result is surely well known, and has an elementary proof which we include for convenience.
Corollary 1.2 Let
![]() $w:[0,1) \to (0,1)$
be any decreasing function satisfying
$w:[0,1) \to (0,1)$
be any decreasing function satisfying
![]() $\lim _{t \to 1^-} w(t) = 0$
. There exist a singular inner function
$\lim _{t \to 1^-} w(t) = 0$
. There exist a singular inner function
![]() $\theta = S_\nu $
and a sequence of analytic polynomials
$\theta = S_\nu $
and a sequence of analytic polynomials
![]() $\{p_n\}_n$
such that:
$\{p_n\}_n$
such that:
-
(1)
 $\lim _{n \to \infty } \theta (z) p_n(z) = 1, \quad z \in \mathbb {D},$
$\lim _{n \to \infty } \theta (z) p_n(z) = 1, \quad z \in \mathbb {D},$
-
(2)
 $\sup _{z \in \mathbb {D}} |\theta (z) p_n(z)| w(|z|) \leq 2$
.
$\sup _{z \in \mathbb {D}} |\theta (z) p_n(z)| w(|z|) \leq 2$
.
Proof Apply Theorem 1.1 to the function w to produce a singular inner function
![]() $\theta $
satisfying (1.3). For integers
$\theta $
satisfying (1.3). For integers
![]() $n \geq 2$
, we set
$n \geq 2$
, we set
![]() $r_n := 1- 1/n$
and
$r_n := 1- 1/n$
and
![]() $Q_n(z) := 1/\theta (r_n z)$
. Then
$Q_n(z) := 1/\theta (r_n z)$
. Then
![]() $Q_n$
is holomorphic in a neighborhood of the closed disk
$Q_n$
is holomorphic in a neighborhood of the closed disk
![]() $\overline {\mathbb {D}}$
, and because we are assuming that w is decreasing, we have the estimate
$\overline {\mathbb {D}}$
, and because we are assuming that w is decreasing, we have the estimate
We can approximate
![]() $Q_n$
by an analytic polynomial
$Q_n$
by an analytic polynomial
![]() $p_n$
so that
$p_n$
so that
Then
It is clear from the construction that
![]() $\theta (z)p_n(z) \to 1$
as
$\theta (z)p_n(z) \to 1$
as
![]() $n \to \infty $
, for any
$n \to \infty $
, for any
![]() $z \in \mathbb {D}$
.
$z \in \mathbb {D}$
.
Corollary 1.2 says that there exist cyclic singular inner functions in essentially any space of analytic functions defined in terms of a growth condition, or in any space in which such a growth space is continuously embedded.
The purpose of this note is to apply Theorem 1.1, or more precisely its simple consequence stated in Corollary 1.2, to the questions of existence of functions with certain smoothness properties in model spaces
![]() $K_\theta $
. We will establish sharpness of certain existing approximation results in these spaces. Moreover, we take the opportunity to discuss similar questions in the broader class of de Branges–Rovnyak spaces
$K_\theta $
. We will establish sharpness of certain existing approximation results in these spaces. Moreover, we take the opportunity to discuss similar questions in the broader class of de Branges–Rovnyak spaces
![]() $\mathcal {H}(b)$
. Our results are proved by rather well-known methods, but their statements seem to be missing in the existing literature, and we wish to fill in this gap.
$\mathcal {H}(b)$
. Our results are proved by rather well-known methods, but their statements seem to be missing in the existing literature, and we wish to fill in this gap.
In the proofs of the main results, which will be stated shortly, we will concern ourselves with the following weak type of cyclicity of singular inner functions. Let Y be some linear space of analytic functions which is contained in
![]() $H^1$
. We want to investigate if there exist a singular inner function
$H^1$
. We want to investigate if there exist a singular inner function
![]() $\theta $
and a sequence of polynomials
$\theta $
and a sequence of polynomials
![]() $\{p_n\}_n$
such that
$\{p_n\}_n$
such that
holds for all
![]() $f \in Y$
. The above situation means that the sequence
$f \in Y$
. The above situation means that the sequence
![]() $\{\theta p_n\}_n$
converges to the constant
$\{\theta p_n\}_n$
converges to the constant
![]() $1$
, weakly over the space Y. Now, clearly, if Y is too large of a space (say,
$1$
, weakly over the space Y. Now, clearly, if Y is too large of a space (say,
![]() $Y = H^2$
), then (1.6) can never hold for all
$Y = H^2$
), then (1.6) can never hold for all
![]() $f \in Y$
. However, if Y is sufficiently small, then the situation in (1.6) might occur. For instance, in the extreme case, when Y is a set of analytic polynomials, then any singular inner function
$f \in Y$
. However, if Y is sufficiently small, then the situation in (1.6) might occur. For instance, in the extreme case, when Y is a set of analytic polynomials, then any singular inner function
![]() $\theta $
and any sequence of polynomials
$\theta $
and any sequence of polynomials
![]() $\{p_n\}_n$
which satisfies
$\{p_n\}_n$
which satisfies
![]() $\lim _{n \to \infty } p_n(z) = 1/\theta (z)$
for
$\lim _{n \to \infty } p_n(z) = 1/\theta (z)$
for
![]() $z \in \mathbb {D}$
is sufficient to make (1.6) hold. Philosophically speaking, it is the uniform smoothness of the functions in the class Y that allows the existence of singular inner functions
$z \in \mathbb {D}$
is sufficient to make (1.6) hold. Philosophically speaking, it is the uniform smoothness of the functions in the class Y that allows the existence of singular inner functions
![]() $\theta $
for which the above situation occurs. Under insignificant assumptions on Y, a straightforward argument shows that if (1.6) occurs, then the intersection between Y and
$\theta $
for which the above situation occurs. Under insignificant assumptions on Y, a straightforward argument shows that if (1.6) occurs, then the intersection between Y and
![]() $K_\theta $
is trivial, whereas Corollary 1.2 provides us with a huge class of spaces Y for which (1.6) can be achieved.
$K_\theta $
is trivial, whereas Corollary 1.2 provides us with a huge class of spaces Y for which (1.6) can be achieved.
1.2 Main results
Recall that the space
![]() $K_\theta $
is constructed from an inner function
$K_\theta $
is constructed from an inner function
![]() $\theta $
by taking the orthogonal complement of the subspace
$\theta $
by taking the orthogonal complement of the subspace
in the Hardy space
![]() $H^2$
:
$H^2$
:
For background on the spaces
![]() $K_\theta $
, one can consult the books [Reference Cima, Matheson and Ross5, Reference Garcia, Mashreghi and Ross9]. In our first result, we will show that the famous approximation theorem of Aleksandrov from [Reference Aleksandrov1] on density in
$K_\theta $
, one can consult the books [Reference Cima, Matheson and Ross5, Reference Garcia, Mashreghi and Ross9]. In our first result, we will show that the famous approximation theorem of Aleksandrov from [Reference Aleksandrov1] on density in
![]() $K_\theta $
of functions which extend continuously to the boundary is in fact essentially sharp, as it cannot be extended to any class of functions satisfying an estimate on their modulus of continuity. By a modulus of continuity
$K_\theta $
of functions which extend continuously to the boundary is in fact essentially sharp, as it cannot be extended to any class of functions satisfying an estimate on their modulus of continuity. By a modulus of continuity
![]() $\omega $
, we mean here a function
$\omega $
, we mean here a function
![]() $\omega : [0,\infty ) \to [0, \infty )$
which is continuous, increasing, satisfies
$\omega : [0,\infty ) \to [0, \infty )$
which is continuous, increasing, satisfies
![]() $\omega (0) = 0$
, and for which
$\omega (0) = 0$
, and for which
![]() $\omega (t)/t$
is a decreasing function with
$\omega (t)/t$
is a decreasing function with
For such a function
![]() $\omega $
, we define
$\omega $
, we define
![]() $\Lambda ^\omega _a$
to be the space of functions f which are analytic in
$\Lambda ^\omega _a$
to be the space of functions f which are analytic in
![]() $\mathbb {D}$
, extend continuously to
$\mathbb {D}$
, extend continuously to
![]() $\overline {\mathbb {D}}$
, and satisfy
$\overline {\mathbb {D}}$
, and satisfy
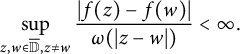 $$ \begin{align} \sup_{z,w \in \overline{\mathbb{D}}, z \neq w} \frac{|f(z)-f(w)|}{\omega(|z-w|)} < \infty. \end{align} $$
$$ \begin{align} \sup_{z,w \in \overline{\mathbb{D}}, z \neq w} \frac{|f(z)-f(w)|}{\omega(|z-w|)} < \infty. \end{align} $$
Then
![]() $\Lambda ^\omega _a$
is the space of analytic functions on
$\Lambda ^\omega _a$
is the space of analytic functions on
![]() $\mathbb {D}$
which have a modulus of continuity dominated by
$\mathbb {D}$
which have a modulus of continuity dominated by
![]() $\omega $
. We make
$\omega $
. We make
![]() $\Lambda ^\omega _a$
into a normed space by introducing the quantity
$\Lambda ^\omega _a$
into a normed space by introducing the quantity
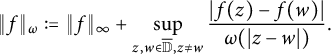 $$ \begin{align*}\|f\|_\omega := \|f\|_\infty + \sup_{z,w \in \overline{\mathbb{D}}, z \neq w} \frac{|f(z)-f(w)|}{\omega(|z-w|)}.\end{align*} $$
$$ \begin{align*}\|f\|_\omega := \|f\|_\infty + \sup_{z,w \in \overline{\mathbb{D}}, z \neq w} \frac{|f(z)-f(w)|}{\omega(|z-w|)}.\end{align*} $$
By a theorem of Tamrazov from [Reference Tamrazov19], we could have replaced the supremum over
![]() $\overline {\mathbb {D}}$
by a supremum over
$\overline {\mathbb {D}}$
by a supremum over
![]() $\mathbb {T}$
, and obtain the same space of functions (we remark that a nice proof of this result is contained in [Reference Bouya4, Appendix A]). The following is an optimality statement regarding Aleksandrov’s density theorem.
$\mathbb {T}$
, and obtain the same space of functions (we remark that a nice proof of this result is contained in [Reference Bouya4, Appendix A]). The following is an optimality statement regarding Aleksandrov’s density theorem.
Theorem 1.3 Let
![]() $\omega $
be a modulus of continuity. There exists a singular inner function
$\omega $
be a modulus of continuity. There exists a singular inner function
![]() $\theta $
such that
$\theta $
such that
This statement will be proved in Section 3. In fact, we will see that Theorem 1.3 is a consequence of a variant, and in some directions a strengthening, of a theorem of Dyakonov and Khavinson from [Reference Dyakonov and Khavinson6]. For a sequence of positive numbers
![]() $\boldsymbol {\lambda } = \{\lambda _n\}_{n=0}^\infty $
, we define the class
$\boldsymbol {\lambda } = \{\lambda _n\}_{n=0}^\infty $
, we define the class
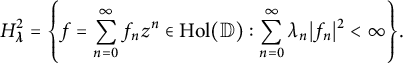 $$ \begin{align} H^2_{\boldsymbol{\lambda}} = \Bigg\{ f = \sum_{n=0}^\infty f_n z^n \in \mathrm{Hol}(\mathbb{D}) : \sum_{n=0}^\infty \lambda_n|f_n|^2 < \infty \Bigg\}. \end{align} $$
$$ \begin{align} H^2_{\boldsymbol{\lambda}} = \Bigg\{ f = \sum_{n=0}^\infty f_n z^n \in \mathrm{Hol}(\mathbb{D}) : \sum_{n=0}^\infty \lambda_n|f_n|^2 < \infty \Bigg\}. \end{align} $$
The next theorem, proved in Section 2, reads as follows.
Theorem 1.4 Let
![]() $\boldsymbol {\lambda } = \{\lambda _n\}_{n=0}^\infty $
be any increasing sequence of positive numbers with
$\boldsymbol {\lambda } = \{\lambda _n\}_{n=0}^\infty $
be any increasing sequence of positive numbers with
![]() $\lim _{n \to \infty } \lambda _n = \infty $
. Then there exists a singular inner function
$\lim _{n \to \infty } \lambda _n = \infty $
. Then there exists a singular inner function
![]() $\theta $
such that
$\theta $
such that
The result can be compared to the mentioned result of Dyakonov and Khavinson in [Reference Dyakonov and Khavinson6], from which the above result can be deduced in the special case
![]() $\boldsymbol {\lambda } = \{ (k+1)^{\alpha }\}_{k=0}^\infty $
with any
$\boldsymbol {\lambda } = \{ (k+1)^{\alpha }\}_{k=0}^\infty $
with any
![]() $\alpha> 0$
.
$\alpha> 0$
.
The theory of de Branges–Rovnyak spaces
![]() $\mathcal {H}(b)$
is a well-known generalization of the theory of model spaces
$\mathcal {H}(b)$
is a well-known generalization of the theory of model spaces
![]() $K_\theta $
. The symbol of the space b is now any analytic self-map of the unit disk, and we have
$K_\theta $
. The symbol of the space b is now any analytic self-map of the unit disk, and we have
![]() $\mathcal {H}(b) = K_b$
whenever b is inner. For background on
$\mathcal {H}(b) = K_b$
whenever b is inner. For background on
![]() $\mathcal {H}(b)$
spaces, one can consult [Reference Sarason16] or [Reference Fricain and Mashreghi7, Reference Fricain and Mashreghi8]. A consequence of the author’s work in collaboration with Aleman in [Reference Aleman and Malman2] is that the abovementioned density theorem of Aleksandrov generalizes to the broader class of
$\mathcal {H}(b)$
spaces, one can consult [Reference Sarason16] or [Reference Fricain and Mashreghi7, Reference Fricain and Mashreghi8]. A consequence of the author’s work in collaboration with Aleman in [Reference Aleman and Malman2] is that the abovementioned density theorem of Aleksandrov generalizes to the broader class of
![]() $\mathcal {H}(b)$
spaces: any such space admits a dense subset of functions which extend continuously to the boundary. Since Theorem 1.3 proves optimality of Aleksandrov’s theorem for inner functions
$\mathcal {H}(b)$
spaces: any such space admits a dense subset of functions which extend continuously to the boundary. Since Theorem 1.3 proves optimality of Aleksandrov’s theorem for inner functions
![]() $\theta $
, one could ask if at least for outer symbols b any improvement of the density result in
$\theta $
, one could ask if at least for outer symbols b any improvement of the density result in
![]() $\mathcal {H}(b)$
from [Reference Aleman and Malman2] can be obtained. In Section 4, we remark that this is not the case, and the result in [Reference Aleman and Malman2] is also essentially optimal, even for outer symbols b.
$\mathcal {H}(b)$
from [Reference Aleman and Malman2] can be obtained. In Section 4, we remark that this is not the case, and the result in [Reference Aleman and Malman2] is also essentially optimal, even for outer symbols b.
Theorem 1.5 Let
![]() $\boldsymbol {\lambda } = \{\lambda _n\}_{n=0}^\infty $
be any increasing sequence of positive numbers with
$\boldsymbol {\lambda } = \{\lambda _n\}_{n=0}^\infty $
be any increasing sequence of positive numbers with
![]() $\lim _{n \to \infty } \lambda _n = \infty $
. There exists an outer function
$\lim _{n \to \infty } \lambda _n = \infty $
. There exists an outer function
![]() $b:\mathbb {D} \to \mathbb {D}$
such that
$b:\mathbb {D} \to \mathbb {D}$
such that
Theorem 1.6 Let
![]() $\omega $
be a modulus of continuity. There exists an outer function
$\omega $
be a modulus of continuity. There exists an outer function
![]() $b:\mathbb {D} \to \mathbb {D}$
such that
$b:\mathbb {D} \to \mathbb {D}$
such that
We will show that the above results are essentially equivalent to a theorem of Khrushchev from [Reference Khrushchev11].
In Section 5, we list a few questions we have not found an answer for, and some ideas for further research.
2 Proof of Theorem 1.4
In the proof of the theorem, we will need to use the following crude construction of an integrable weight with large moments.
Lemma 2.1 Let
![]() $\{\lambda _n\}_{n=0}^\infty $
be a decreasing sequence of positive numbers with
$\{\lambda _n\}_{n=0}^\infty $
be a decreasing sequence of positive numbers with
![]() $\lim _{n \to \infty } \lambda _n = 0$
. There exists a nonnegative function
$\lim _{n \to \infty } \lambda _n = 0$
. There exists a nonnegative function
![]() $\Lambda \in L^1([0,1])$
which satisfies
$\Lambda \in L^1([0,1])$
which satisfies
Proof Recall that the sequence
![]() $(1-1/n)^n = \exp (n\log (1-1/n))$
is decreasing and satisfies
$(1-1/n)^n = \exp (n\log (1-1/n))$
is decreasing and satisfies
It follows that
for some constant
![]() $\alpha> 0$
which is independent of n. For
$\alpha> 0$
which is independent of n. For
![]() $n \geq 1$
, we define the intervals
$n \geq 1$
, we define the intervals
![]() $I_n = \big ( 1 - 1/n, 1 - 1/(n+1) \big )$
. Our function
$I_n = \big ( 1 - 1/n, 1 - 1/(n+1) \big )$
. Our function
![]() $\Lambda $
will be chosen to be of the form
$\Lambda $
will be chosen to be of the form
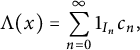 $$ \begin{align*}\Lambda(x) = \sum_{n=0}^\infty 1_{I_n} c_n,\end{align*} $$
$$ \begin{align*}\Lambda(x) = \sum_{n=0}^\infty 1_{I_n} c_n,\end{align*} $$
where
![]() $1_{I_n}$
is the indicator function of the interval
$1_{I_n}$
is the indicator function of the interval
![]() $I_n$
and the
$I_n$
and the
![]() $c_n$
are positive constants to be chosen shortly. Note that
$c_n$
are positive constants to be chosen shortly. Note that
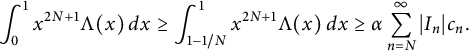 $$ \begin{align} \int_0^1 x^{2N+1} \Lambda(x) \, dx \geq \int_{1-1/N}^1 x^{2N+1} \Lambda(x) \, dx \geq \alpha \sum_{n = N}^\infty |I_n| c_n. \end{align} $$
$$ \begin{align} \int_0^1 x^{2N+1} \Lambda(x) \, dx \geq \int_{1-1/N}^1 x^{2N+1} \Lambda(x) \, dx \geq \alpha \sum_{n = N}^\infty |I_n| c_n. \end{align} $$
We choose
This choice of coefficients
![]() $c_n$
makes
$c_n$
makes
![]() $\Lambda $
integrable over
$\Lambda $
integrable over
![]() $[0,1]$
:
$[0,1]$
:
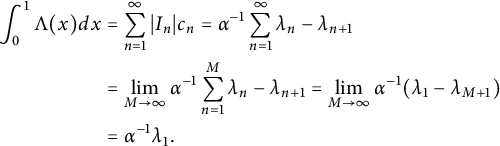 $$ \begin{align*} \int_{0}^1 \Lambda(x) dx &= \sum_{n=1}^\infty |I_n|c_n = \alpha^{-1} \sum_{n=1}^\infty \lambda_n - \lambda_{n+1} \\&= \lim_{M \to \infty} \alpha^{-1} \sum_{n=1}^M \lambda_n - \lambda_{n+1} = \lim_{M \to \infty} \alpha^{-1} (\lambda_1 - \lambda_{M+1}) \\& = \alpha^{-1} \lambda_1. \end{align*} $$
$$ \begin{align*} \int_{0}^1 \Lambda(x) dx &= \sum_{n=1}^\infty |I_n|c_n = \alpha^{-1} \sum_{n=1}^\infty \lambda_n - \lambda_{n+1} \\&= \lim_{M \to \infty} \alpha^{-1} \sum_{n=1}^M \lambda_n - \lambda_{n+1} = \lim_{M \to \infty} \alpha^{-1} (\lambda_1 - \lambda_{M+1}) \\& = \alpha^{-1} \lambda_1. \end{align*} $$
In the last step, we used the assumption that the sequence
![]() $\{\lambda _n\}_n$
converges to zero. Moreover, by (2.1) and the choice of
$\{\lambda _n\}_n$
converges to zero. Moreover, by (2.1) and the choice of
![]() $c_n$
, we can estimate
$c_n$
, we can estimate
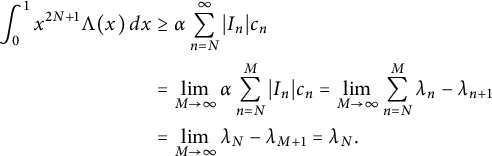 $$ \begin{align*}\int_0^1 x^{2N+1} \Lambda(x) \, dx &\geq \alpha \sum_{n=N}^\infty |I_n|c_n \\&= \lim_{M \to \infty} \alpha \sum_{n=N}^M |I_n| c_n = \lim_{M \to \infty} \sum_{n=N}^M \lambda_n -\lambda_{n+1} \\&= \lim_{M \to \infty} \lambda_N - \lambda_{M+1} = \lambda_N.\end{align*} $$
$$ \begin{align*}\int_0^1 x^{2N+1} \Lambda(x) \, dx &\geq \alpha \sum_{n=N}^\infty |I_n|c_n \\&= \lim_{M \to \infty} \alpha \sum_{n=N}^M |I_n| c_n = \lim_{M \to \infty} \sum_{n=N}^M \lambda_n -\lambda_{n+1} \\&= \lim_{M \to \infty} \lambda_N - \lambda_{M+1} = \lambda_N.\end{align*} $$
The proof is complete.
The significance of the above lemma is the estimate
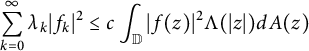 $$ \begin{align} \sum_{k=0}^\infty \lambda_k|f_k|^2 \leq c \int_{\mathbb{D}} |f(z)|^2 \Lambda(|z|) dA(z) \end{align} $$
$$ \begin{align} \sum_{k=0}^\infty \lambda_k|f_k|^2 \leq c \int_{\mathbb{D}} |f(z)|^2 \Lambda(|z|) dA(z) \end{align} $$
for some numerical constant
![]() $c> 0$
and any function f which is holomorphic in a neighborhood of the closed disk
$c> 0$
and any function f which is holomorphic in a neighborhood of the closed disk
![]() $\overline {\mathbb {D}}$
. The estimate can be verified by direct computation of the integral on the right-hand side, using polar coordinates.
$\overline {\mathbb {D}}$
. The estimate can be verified by direct computation of the integral on the right-hand side, using polar coordinates.
We will also use the following well-known construction.
Lemma 2.2 For any function
![]() $g \in L^1([0,1])$
, there exists a positive and increasing function
$g \in L^1([0,1])$
, there exists a positive and increasing function
![]() $w: [0,1) \to \mathbb {R}$
which satisfies
$w: [0,1) \to \mathbb {R}$
which satisfies
and
Proof The integrability condition on g implies that
Thus, there exists a sequence of intervals
![]() $\{I_n\}_{n=1}^\infty $
which have
$\{I_n\}_{n=1}^\infty $
which have
![]() $1$
as the right endpoint and length shrinking to zero, which satisfy
$1$
as the right endpoint and length shrinking to zero, which satisfy
![]() $I_{n+1} \subset I_n$
for all
$I_{n+1} \subset I_n$
for all
![]() $n \geq 1$
, and
$n \geq 1$
, and
If we set
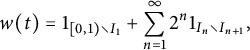 $$ \begin{align*}w(t) = 1_{[0,1) \setminus I_1} + \sum_{n=1}^\infty 2^n 1_{I_n \setminus I_{n+1}},\end{align*} $$
$$ \begin{align*}w(t) = 1_{[0,1) \setminus I_1} + \sum_{n=1}^\infty 2^n 1_{I_n \setminus I_{n+1}},\end{align*} $$
where
![]() $1_{I_n \setminus I_{n+1}}$
is the indicator function of the set difference
$1_{I_n \setminus I_{n+1}}$
is the indicator function of the set difference
![]() $I_n \setminus I_{n+1}$
, then w is increasing, satisfies
$I_n \setminus I_{n+1}$
, then w is increasing, satisfies
![]() $\lim _{t \to 1^-} w(t) = \infty $
, and
$\lim _{t \to 1^-} w(t) = \infty $
, and
for all
![]() $n \geq 1$
. Consequently,
$n \geq 1$
. Consequently,
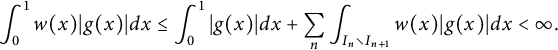 $$ \begin{align*}\int_{0}^1 w(x)|g(x)|dx \leq \int_{0}^1 |g(x)|dx + \sum_{n} \int_{I_n \setminus I_{n+1}} w(x)|g(x)| dx < \infty.\\[-40pt] \end{align*} $$
$$ \begin{align*}\int_{0}^1 w(x)|g(x)|dx \leq \int_{0}^1 |g(x)|dx + \sum_{n} \int_{I_n \setminus I_{n+1}} w(x)|g(x)| dx < \infty.\\[-40pt] \end{align*} $$
Proof of Theorem 1.4
Let
![]() $\Lambda $
be the function in Lemma 2.1 which corresponds to the sequence
$\Lambda $
be the function in Lemma 2.1 which corresponds to the sequence
![]() $\{1/\lambda _n\}_{n=0}^\infty $
. That is,
$\{1/\lambda _n\}_{n=0}^\infty $
. That is,
![]() $\Lambda $
satisfies
$\Lambda $
satisfies
and
![]() $\Lambda \in L^1[0,1]$
. Now, let w be a positive decreasing function which satisfies
$\Lambda \in L^1[0,1]$
. Now, let w be a positive decreasing function which satisfies
![]() $w(x) < 1/2$
,
$w(x) < 1/2$
,
![]() $\lim _{x \to 1^-} w(x) = 0$
and
$\lim _{x \to 1^-} w(x) = 0$
and
Existence of such a function follows readily from Lemma 2.2. Apply Corollary 1.2 to w and obtain a corresponding inner function
![]() $\theta $
and a sequence of polynomials
$\theta $
and a sequence of polynomials
![]() $\{p_n\}_n$
for which the conclusions (i) and (ii) of Corollary 1.2 hold. We will show that for this
$\{p_n\}_n$
for which the conclusions (i) and (ii) of Corollary 1.2 hold. We will show that for this
![]() $\theta $
, we have
$\theta $
, we have
![]() $K_\theta \cap H^2_{\boldsymbol {\lambda }} = \{0\}.$
$K_\theta \cap H^2_{\boldsymbol {\lambda }} = \{0\}.$
Indeed, assume that
![]() $f \in K_\theta \cap H^2_{\boldsymbol {\lambda }} = \{0\},$
but that in fact f is nonzero. Since both
$f \in K_\theta \cap H^2_{\boldsymbol {\lambda }} = \{0\},$
but that in fact f is nonzero. Since both
![]() $K_\theta $
and
$K_\theta $
and
![]() $H^2_{\boldsymbol {\lambda }}$
are invariant for the backward shift operator, we may without loss of generality assume that
$H^2_{\boldsymbol {\lambda }}$
are invariant for the backward shift operator, we may without loss of generality assume that
![]() $f(0) \neq 0$
. Fix an integer n, and let
$f(0) \neq 0$
. Fix an integer n, and let
Let
![]() $\{f_k\}_k, \{g_k\}_k$
be the sequences of Taylor coefficients of f and g, respectively. Since
$\{f_k\}_k, \{g_k\}_k$
be the sequences of Taylor coefficients of f and g, respectively. Since
![]() $f \in K_\theta $
, we have
$f \in K_\theta $
, we have
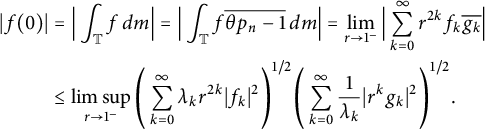 $$ \begin{align*} |f(0)| &= \Big\vert \int_{\mathbb{T}} f \, d\textit{m} \Big\vert = \Big\vert \int_{\mathbb{T}} f\overline{\theta p_n - 1} \, d\textit{m}\Big\vert = \lim_{r \to 1^-} \Big\vert \sum_{k=0}^\infty r^{2k} f_k \overline{g_k} \Big\vert \\ &\leq \limsup_{r \to 1^-}\Bigg( \sum_{k=0}^\infty \lambda_k r^{2k} |f_k|^2 \Bigg)^{1/2} \Bigg( \sum_{k=0}^\infty \frac{1}{\lambda_k} |r^k g_k|^2 \Bigg)^{1/2}. \\ \end{align*} $$
$$ \begin{align*} |f(0)| &= \Big\vert \int_{\mathbb{T}} f \, d\textit{m} \Big\vert = \Big\vert \int_{\mathbb{T}} f\overline{\theta p_n - 1} \, d\textit{m}\Big\vert = \lim_{r \to 1^-} \Big\vert \sum_{k=0}^\infty r^{2k} f_k \overline{g_k} \Big\vert \\ &\leq \limsup_{r \to 1^-}\Bigg( \sum_{k=0}^\infty \lambda_k r^{2k} |f_k|^2 \Bigg)^{1/2} \Bigg( \sum_{k=0}^\infty \frac{1}{\lambda_k} |r^k g_k|^2 \Bigg)^{1/2}. \\ \end{align*} $$
Using inequality (2.2) on the term on the right-hand side in the last expression (with
![]() $\lambda _n$
replaced by
$\lambda _n$
replaced by
![]() $1/\lambda _n$
), we obtain
$1/\lambda _n$
), we obtain
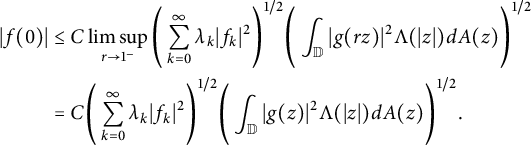 $$ \begin{align*} |f(0)| &\leq C \limsup_{r \to 1^-} \Bigg( \sum_{k=0}^\infty \lambda_k |f_k|^2 \Bigg)^{1/2} \Bigg(\int_{\mathbb{D}} |g(rz)|^2 \Lambda(|z|)d A(z) \Bigg)^{1/2} \\ &= C \Bigg( \sum_{k=0}^\infty \lambda_k |f_k|^2 \Bigg)^{1/2} \Bigg(\int_{\mathbb{D}} |g(z)|^2 \Lambda(|z|)d A(z) \Bigg)^{1/2}. \end{align*} $$
$$ \begin{align*} |f(0)| &\leq C \limsup_{r \to 1^-} \Bigg( \sum_{k=0}^\infty \lambda_k |f_k|^2 \Bigg)^{1/2} \Bigg(\int_{\mathbb{D}} |g(rz)|^2 \Lambda(|z|)d A(z) \Bigg)^{1/2} \\ &= C \Bigg( \sum_{k=0}^\infty \lambda_k |f_k|^2 \Bigg)^{1/2} \Bigg(\int_{\mathbb{D}} |g(z)|^2 \Lambda(|z|)d A(z) \Bigg)^{1/2}. \end{align*} $$
By assertion in part (ii) of Corollary 1.2, the function
![]() $|g(z)|^2\Lambda (|z|)$
is dominated pointwise in
$|g(z)|^2\Lambda (|z|)$
is dominated pointwise in
![]() $\mathbb {D}$
by the integrable function
$\mathbb {D}$
by the integrable function
independently of which polynomial
![]() $p_n$
is used to defined g in (2.3). However, if we let
$p_n$
is used to defined g in (2.3). However, if we let
![]() $n \to \infty $
in (2.3), then
$n \to \infty $
in (2.3), then
![]() $|g(z)|^2\Lambda (|z|) \to 0$
, and so we infer from the computation above and the dominated convergence theorem that
$|g(z)|^2\Lambda (|z|) \to 0$
, and so we infer from the computation above and the dominated convergence theorem that
![]() $f(0) = 0$
, which is a contradiction. The conclusion is that
$f(0) = 0$
, which is a contradiction. The conclusion is that
![]() $K_\theta \cap H^2_{\boldsymbol {\lambda }} = \{ 0\}$
, and the proof of the theorem is complete.
$K_\theta \cap H^2_{\boldsymbol {\lambda }} = \{ 0\}$
, and the proof of the theorem is complete.
3 Proof of Theorem 1.3
Theorem 1.3 will follow immediately from Theorem 1.4 together with the following embedding result for the spaces
![]() $\Lambda ^\omega _a$
.
$\Lambda ^\omega _a$
.
Lemma 3.1 Let
![]() $\omega $
be a modulus of continuity. There exists an increasing sequence of positive numbers
$\omega $
be a modulus of continuity. There exists an increasing sequence of positive numbers
![]() $\boldsymbol {\alpha } = \{ \alpha _n\}_{n=0}^\infty $
satisfying
$\boldsymbol {\alpha } = \{ \alpha _n\}_{n=0}^\infty $
satisfying
![]() $\lim _{n \to \infty } \alpha _n = \infty $
such that for any
$\lim _{n \to \infty } \alpha _n = \infty $
such that for any
![]() $f \in \Lambda ^\omega _a$
we have the estimate
$f \in \Lambda ^\omega _a$
we have the estimate
where
![]() $C> 0$
is a numerical constant and
$C> 0$
is a numerical constant and
![]() $\{f_n\}_n$
is the sequence of Taylor coefficients of f.
$\{f_n\}_n$
is the sequence of Taylor coefficients of f.
Proof For each
![]() $r \in (0,1)$
, we have the estimate
$r \in (0,1)$
, we have the estimate
Since
![]() $\lim _{t \to 0} \omega (t) = 0$
, for each positive integer N, there exists a number
$\lim _{t \to 0} \omega (t) = 0$
, for each positive integer N, there exists a number
![]() $r_N \in (0,1)$
such that
$r_N \in (0,1)$
such that
![]() $\omega (1-r_N) \leq \frac {1}{2^N}$
. Since
$\omega (1-r_N) \leq \frac {1}{2^N}$
. Since
![]() $\lim _{n \to \infty } r_N^{2n} = 0$
, there exists an integer
$\lim _{n \to \infty } r_N^{2n} = 0$
, there exists an integer
![]() $K(N)$
such that
$K(N)$
such that
![]() $r_N^{2n} < 1/2$
for
$r_N^{2n} < 1/2$
for
![]() $n \geq K(N)$
. Then
$n \geq K(N)$
. Then
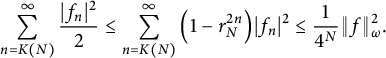 $$ \begin{align*} \sum_{n = K(N)}^\infty \frac{|f_n|^2}{2} \leq \sum_{n=K(N)}^\infty \Big(1-r_N^{2n}\Big)|f_n|^2 \leq \frac{1}{4^N}\|f\|^2_\omega. \end{align*} $$
$$ \begin{align*} \sum_{n = K(N)}^\infty \frac{|f_n|^2}{2} \leq \sum_{n=K(N)}^\infty \Big(1-r_N^{2n}\Big)|f_n|^2 \leq \frac{1}{4^N}\|f\|^2_\omega. \end{align*} $$
Consequently,
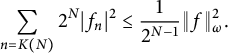 $$ \begin{align} \sum_{n=K(N)} 2^N |f_n|^2 \leq \frac{1}{2^{N-1}} \|f\|^2_\omega. \end{align} $$
$$ \begin{align} \sum_{n=K(N)} 2^N |f_n|^2 \leq \frac{1}{2^{N-1}} \|f\|^2_\omega. \end{align} $$
We can clearly choose the sequence of integers
![]() $K(N)$
to be increasing with N. If we define the sequence
$K(N)$
to be increasing with N. If we define the sequence
![]() $\boldsymbol {\alpha }$
by the equation
$\boldsymbol {\alpha }$
by the equation
![]() $\alpha _n = 1$
for
$\alpha _n = 1$
for
![]() $n < K(1)$
, and
$n < K(1)$
, and
![]() $\alpha _n = 2^N$
for
$\alpha _n = 2^N$
for
![]() $K(N) \leq n < K(N+1)$
, then (3.1) follows readily from (3.3) by summing over all
$K(N) \leq n < K(N+1)$
, then (3.1) follows readily from (3.3) by summing over all
![]() $N \geq 1$
.
$N \geq 1$
.
Proof of Theorem 1.3
Lemma 3.1 implies that
![]() $\Lambda ^\omega _a$
is contained in some space of the form
$\Lambda ^\omega _a$
is contained in some space of the form
![]() $H^2_{\boldsymbol {\alpha }}$
as defined in (1.8). If
$H^2_{\boldsymbol {\alpha }}$
as defined in (1.8). If
![]() $\theta $
is a singular inner function given by Theorem 1.4 such that
$\theta $
is a singular inner function given by Theorem 1.4 such that
![]() $H^2_{\boldsymbol {\alpha }} \cap K_\theta = \{0\}$
, then obviously we also have that
$H^2_{\boldsymbol {\alpha }} \cap K_\theta = \{0\}$
, then obviously we also have that
![]() $\Lambda ^\omega _a \cap K_\theta = \{0\}$
, and so the claim follows.
$\Lambda ^\omega _a \cap K_\theta = \{0\}$
, and so the claim follows.
4 Proofs of Theorems 1.5 and 1.6
Here, we prove the optimality of the continuous approximation theorem for the larger class of
![]() $\mathcal {H}(b)$
-spaces. As remarked in the introduction, this is essentially equivalent to a theorem of Khrushchev from [Reference Khrushchev11].
$\mathcal {H}(b)$
-spaces. As remarked in the introduction, this is essentially equivalent to a theorem of Khrushchev from [Reference Khrushchev11].
Proof of Theorem 1.5
By a result of Khrushchev noted in [Reference Khrushchev11, Theorem 2.4], there exists a closed subset E of the circle
![]() $\mathbb {T}$
with the property that for no nonzero integrable function h supported on E is the Cauchy integral
$\mathbb {T}$
with the property that for no nonzero integrable function h supported on E is the Cauchy integral
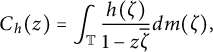 $$\begin{align*}C_h(z) = \int_{\mathbb{T}} \frac{h(\zeta)}{1-z\overline{\zeta}} d\textit{m}(\zeta),\end{align*}$$
$$\begin{align*}C_h(z) = \int_{\mathbb{T}} \frac{h(\zeta)}{1-z\overline{\zeta}} d\textit{m}(\zeta),\end{align*}$$
a member of the space
![]() $H^2_{\boldsymbol {\lambda }}$
. It suffices thus to construct an
$H^2_{\boldsymbol {\lambda }}$
. It suffices thus to construct an
![]() $\mathcal {H}(b)$
space for which every function can be expressed as such a Cauchy integral. The simplest choice for the space symbol b is the outer function with modulus
$\mathcal {H}(b)$
space for which every function can be expressed as such a Cauchy integral. The simplest choice for the space symbol b is the outer function with modulus
![]() $1$
on
$1$
on
![]() $\mathbb {T} \setminus E$
and
$\mathbb {T} \setminus E$
and
![]() $1/2$
on E. Then b is invertible in the algebra
$1/2$
on E. Then b is invertible in the algebra
![]() $H^\infty $
, and a consequence of the general theory (see [Reference Fricain and Mashreghi8, Theorems 20.1 and 28.1]) is that every function in the space
$H^\infty $
, and a consequence of the general theory (see [Reference Fricain and Mashreghi8, Theorems 20.1 and 28.1]) is that every function in the space
![]() $\mathcal {H}(b)$
is a Cauchy integral of a function h which is square-integrable on
$\mathcal {H}(b)$
is a Cauchy integral of a function h which is square-integrable on
![]() $\mathbb {T}$
and supported only on E. Thus,
$\mathbb {T}$
and supported only on E. Thus,
![]() $H^2_{\boldsymbol {\lambda }} \cap \mathcal {H}(b) = \{ 0 \}$
, by Khrushchev’s theorem.
$H^2_{\boldsymbol {\lambda }} \cap \mathcal {H}(b) = \{ 0 \}$
, by Khrushchev’s theorem.
Finally, Theorem 1.6 follows from Theorem 1.5 in the same way as Theorem 1.3 follows from Theorem 1.4.
5 Some ending questions and remarks
Since Theorem 1.1 seems to be such a powerful tool in establishing results of the kind mentioned here, we are wondering whether it can be further applied. In particular, the following questions come to mind.
-
(1) Are our methods strong enough to prove that there exist model spaces
 $K_\theta $
which admit no nonzero functions in the Wiener algebra of absolutely convergent Fourier series? The result is known, and has been noted in [Reference Limani and Malman13]. However, it was proved as a consequence of a complicated construction of a cyclic singular inner function in the Bloch space. Is it so that the construction in Corollary 1.2 is sufficient to prove the nondensity result for the Wiener algebra in the fashion presented here?
$K_\theta $
which admit no nonzero functions in the Wiener algebra of absolutely convergent Fourier series? The result is known, and has been noted in [Reference Limani and Malman13]. However, it was proved as a consequence of a complicated construction of a cyclic singular inner function in the Bloch space. Is it so that the construction in Corollary 1.2 is sufficient to prove the nondensity result for the Wiener algebra in the fashion presented here? -
(2) For
 $p> 2$
, the Banach spaces
$p> 2$
, the Banach spaces
 $\ell ^p_a$
consisting of functions
$\ell ^p_a$
consisting of functions
 $f\in Hol(\mathbb {D})$
with Taylor series
$f\in Hol(\mathbb {D})$
with Taylor series
 $\{f_n\}_{n=0}^\infty $
satisfying
$\{f_n\}_{n=0}^\infty $
satisfying  $$ \begin{align*}\|f\|^p_{\ell^p_a} := \sum_{n=0}^\infty |f_n|^p < \infty\end{align*} $$
$$ \begin{align*}\|f\|^p_{\ell^p_a} := \sum_{n=0}^\infty |f_n|^p < \infty\end{align*} $$
are of course larger than the space
 $H^2 = \ell ^2_a$
. Do there exist cyclic singular inner functions in these spaces?
$H^2 = \ell ^2_a$
. Do there exist cyclic singular inner functions in these spaces?
Acknowledgment
The author would like to thank Christopher Felder for his reading of the manuscript and for his helpful suggestions for improvements. He would also like to thank Adem Limani for very useful discussions and important comments.