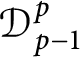 $\mathcal {D}^{p}_{p-1 }$ into tent spaces and Volterra operators
$\mathcal {D}^{p}_{p-1 }$ into tent spaces and Volterra operatorsPublished online by Cambridge University Press: 08 September 2020
In this paper, we study the boundedness and compactness of the inclusion mapping from Dirichlet type spaces
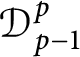 $\mathcal {D}^{p}_{p-1 }$
to tent spaces. Meanwhile, the boundedness, compactness, and essential norm of Volterra integral operators from Dirichlet type spaces
$\mathcal {D}^{p}_{p-1 }$
to tent spaces. Meanwhile, the boundedness, compactness, and essential norm of Volterra integral operators from Dirichlet type spaces
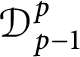 $\mathcal {D}^{p}_{p-1 }$
to general function spaces are also investigated.
$\mathcal {D}^{p}_{p-1 }$
to general function spaces are also investigated.
This work was supported by NNSF of China (Nos. 11801250, 11871257, and 11701222), Overseas Scholarship Program for Elite Young and Middle-aged Teachers of Lingnan Normal University, Yanling Youqing Program of Lingnan Normal University, the Key Program of Lingnan Normal University (No. LZ1905), and Department of Education of Guangdong Province (No. 2018KTSCX133). Xiangling Zhu is the corresponding author.