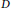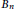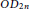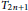Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Ellingham, Mark N.
and
Ellis-Monaghan, Joanna A.
2022.
A Catalog of Enumeration Formulas for Bouquet and Dipole Embeddings under Symmetries.
Symmetry,
Vol. 14,
Issue. 9,
p.
1793.