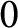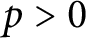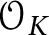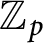Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
He, Tongmu
2025.
Perfectoidness via Sen theory and applications to Shimura varieties.
Journal of the American Mathematical Society,
Vol. 39,
Issue. 1,
p.
95.
He, Tongmu
2025.
Sen operators and Lie algebras arising from Galois representations over p-adic varieties.
Mathematische Zeitschrift,
Vol. 309,
Issue. 3,