Hostname: page-component-cb9f654ff-p5m67 Total loading time: 0 Render date: 2025-08-24T14:01:20.825Z Has data issue: false hasContentIssue false
  • English
  • Français

Finite descent obstruction for Hilbert modular varieties

Part of: Arithmetic problems. Diophantine geometry Arithmetic algebraic geometry Discontinuous groups and automorphic forms

Published online by Cambridge University Press:  22 July 2020

Gregorio Baldi  and
Giada Grossi
Gregorio Baldi
Affiliation:
Department of Mathematics, University College London, 25, Gordon St., London, UK, WC1H 0AY e-mail: gregorio.baldi.16@ucl.ac.uk
Giada Grossi*
Affiliation:
Department of Mathematics, University College London, 25, Gordon St., London, UK, WC1H 0AY e-mail: gregorio.baldi.16@ucl.ac.uk
*
e-mail: giada.grossi.16@ucl.ac.uk
Get access Rights & Permissions [Opens in a new window]

Abstract

Let S be a finite set of primes. We prove that a form of finite Galois descent obstruction is the only obstruction to the existence of 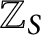$\mathbb {Z}_{S}$-points on integral models of Hilbert modular varieties, extending a result of D. Helm and F. Voloch about modular curves. Let L be a totally real field. Under (a special case of) the absolute Hodge conjecture and a weak Serre’s conjecture for mod $\ell $ representations of the absolute Galois group of L, we prove that the same holds also for the 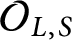$\mathcal {O}_{L,S}$-points.

Keywords

Hilbert modular varietiesdescent obstructionGalois representationsSerre’s conjectureAbelian varieties of GL2-typetotally real fields

MSC classification

Primary: 11F41: Automorphic forms on $(2)$; Hilbert and Hilbert-Siegel modular groups and their modular and automorphic forms; Hilbert modular surfaces 11G35: Varieties over global fields 14G35: Modular and Shimura varieties 11F80: Galois representations

Information

Type
Article
Information
Canadian Mathematical Bulletin , Volume 64 , Issue 2 , June 2021 , pp. 452 - 473
Check for updates
Copyright
© Canadian Mathematical Society 2020

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

Footnotes

This work was supported by the Engineering and Physical Sciences Research Council [EP/ L015234/1], the EPSRC Centre for Doctoral Training in Geometry and Number Theory (The London School of Geometry and Number Theory), and University College London.

References

Allen, P. B., Calegari, F., Caraiani, A., Gee, T., Helm, D., Le Hung, B. V., Newton, J., Scholze, P., Taylor, R., and Thorne, J. A., Potential automorphy over CM fields. Preprint, 2018. arXiv:1812.09999.Google Scholar
Baily, W. L. Jr and Borel, A., Compactification of arithmetic quotients of bounded symmetric domains . Ann. Math 84(1966), 442–528. http://dx.doi.org/10.2307/1970457 CrossRefGoogle Scholar
Baldi, G., Local to global principle for the moduli space of K3 surfaces . Arch. Math. 112(2019), 599–613. http://dx.doi.org/10.1007/s00013-018-01295-1 CrossRefGoogle Scholar
Baldi, G., On the geometric Mumford-Tate conjecture for subvarieties of Shimura varieties . Proc. Amer. Math. Soc. 148(2020), 95–102. http://dx.doi.org/10.1090/proc/14717 CrossRefGoogle Scholar
Barnet-Lamb, T., Gee, T., Geraghty, D., and Taylor, R., Potential automorphy and change of weight . Ann. Math. 179(2014), no. 2, 501–609. http://dx.doi.org/10.4007/annals.2014.179.2.3 CrossRefGoogle Scholar
Blasius, D., Elliptic curves, Hilbert modular forms, and the Hodge conjecture . In: Contributions to automorphic forms, geometry, and number theory, Johns Hopkins University Press, Baltimore, MD, 2004, pp. 83–103.Google Scholar
Blasius, D. and Rogawski, J., Galois representations for Hilbert modular forms . Bull. Amer. Math. Soc. 21(1989), 65–69. http://dx.doi.org/10.1090/S0273-0979-1989-15763-7 CrossRefGoogle Scholar
Borel, A. and Wallach, N., Continuous cohomology, discrete subgroups, and representations of reductive groups . 2nd ed., Mathematical Surveys and Monographs, 67, American Mathematical Society, Providence, RI, 2000. http://dx.doi.org/10.1090/surv/067 CrossRefGoogle Scholar
Buzzard, K., Potential modularity—a survey . In: Non-abelian fundamental groups and Iwasawa theory, London Math. Soc. Lecture Note Ser., 393, Cambridge University Press, Cambridge, UK, 2012, pp. 188–211.Google Scholar
Buzzard, K., Diamond, F., and Jarvis, F., On Serre’s conjecture for mod $\ell$ Galois representations over totally real fields . Duke Math. J. 155(2010), 105–161. http://dx.doi.org/10.1215/00127094-2010-052 CrossRefGoogle Scholar
Carayol, H., Sur les représentations $l$ -adiques associées aux formes modulaires de Hilbert . Ann. Sci. École Norm. Sup. 19(1986), no. 4, 409–468.CrossRefGoogle Scholar
Clozel, L., Motives and automorphic representations . In: Autour des motifs—École d’été Franco-Asiatique de Géométrie Algébrique et de Théorie des Nombres/Asian-French Summer School on Algebraic Geometry and Number Theory. Vol. III, Panor. Synthèses, 49, Société Mathématique de France, Paris, 2016, pp. 29–60.Google Scholar
Cohen, P. B., Itzykson, C., and Wolfart, J., Fuchsian triangle groups and Grothendieck dessins. Variations on a theme of Belyĭ . Comm. Math. Phys. 163(1994), 605–627.CrossRefGoogle Scholar
Deligne, P., Cohomologie étale. Séminaire de géométrie algébrique du Bois-Marie SGA 4 1/2 . Lecture Notes in Mathematics, 569, Springer-Verlag, Berlin, Germany, 1977. http://dx.doi.org/10.1007/BFb0091526 Google Scholar
Deligne, P., Variétés de Shimura: interprétation modulaire, et techniques de construction de modèles canoniques . In: Automorphic forms, representations and L-functions (Proc. Sympos. Pure Math., Oregon State Univ., Corvallis, Or., 1977), Part 2, Proc. Sympos. Pure Math., XXXIII, American Mathematical Society, Providence, RI, 1979, pp. 247–289.Google Scholar
Deligne, P., Milne, J. S., Ogus, A., and Shih, K.-Y., Hodge cycles, motives, and Shimura varieties . Lecture Notes in Mathematics, 900, Springer-Verlag, Berlin, Germany-New York, NY, 1982.Google Scholar
Edixhoven, B., On the André-Oort conjecture for Hilbert modular surfaces . In: Moduli of abelian varieties (Texel Island, 1999). Progr. Math., 195, Birkhäuser, Basel, 2001, pp. 133–155.CrossRefGoogle Scholar
Faltings, G., Endlichkeitssätze für abelsche Varietäten über Zahlkörpern . Invent. Math. 73(1983), 349–366. http://dx.doi.org/10.1007/BF01388432 CrossRefGoogle Scholar
Fontaine, J.-M. and Mazur, B., Geometric Galois representations. In: Elliptic curves, modular forms, & Fermat’s last theorem (Hong Kong, 1993), Ser. Number Theory, I, International Press, Cambridge, MA, 1995, pp. 41–78.Google Scholar
Freitag, E., Hilbert modular forms . Springer-Verlag, Berlin, Germany, 1990. http://dx.doi.org/10.1007/987-3-662-02638-0 CrossRefGoogle Scholar
Freitas, N., Le Hung, B. V., and Siksek, S., Elliptic curves over real quadratic fields are modular . Invent. Math. 201(2015), 159–206. http://dx.doi.org/10.1007/s00222-014-0550-z CrossRefGoogle Scholar
Fujiwara, K., Level optimization in the totally real case. Preprint, 2006. arXiv:math/0602586 Google Scholar
Gee, T., Liu, T., and Savitt, D., The weight part of Serre’s conjecture for $GL(2)$ . Forum Math. Pi 3(2015), e2, 52. http://dx.doi.org/10.1017/fmp.2015.1 CrossRefGoogle Scholar
Goren, E. Z., Lectures on Hilbert modular varieties and modular forms. CRM Monograph Series, 14, American Mathematical Society, Providence, RI, 2002.Google Scholar
Harari, D. and Voloch, J. F., The Brauer-Manin obstruction for integral points on curves . Math. Proc. Camb. Philos. Soc. 149(2010), 413–421. http://dx.doi.org/10.1017/S0305004110000381 CrossRefGoogle Scholar
Helm, D. and Voloch, J. F., Finite descent obstruction on curves and modularity . Bull. Lond. Math. Soc. 43(2011), 805–810. http://dx.doi.org/10.1112/blms/bdr015 CrossRefGoogle Scholar
Khare, C. and Wintenberger, J.-P., On Serre’s conjecture for 2-dimensional mod $p$ representations of ${\mathsf{Gal}} (\overline{\mathbb{Q}}/ \mathbb{Q})$ . Ann. of Math. (2) 169(2009), 229–253. http://dx.doi.org/10.4007/annals.2009.169.229 CrossRefGoogle Scholar
Klevdal, C., Recognizing Galois representations of K3 surfaces . Res. Numb. Theory 5(2019), 12–16. http://dx.doi.org/10.1007/s40993-019-0154-1 Google Scholar
Langlands, R. P., Base change for GL(2) . Annals of Mathematics Studies, 96, Princeton University Press, Princeton, NJ, and University of Tokyo Press, Tokyo, 1980.Google Scholar
Martin-Deschamps, M., La construction de Kodaira–Parshin. Seminar on arithmetic bundles: the Mordell conjecture (Paris, 1983/84). Astérisque 127(1985), 261–273.Google Scholar
Oda, T., Periods of Hilbert modular surfaces. Progress in Mathematics, 19, Birkhäuser, Boston, MA, 1982.CrossRefGoogle Scholar
Patrikis, S., Voloch, J. F., and Zarhin, Y. G., Anabelian geometry and descent obstructions on moduli spaces . Algebra Number Theory 10(2016), 1191–1219. http://dx.doi.org/10.2140/ant.2016.10.1191 CrossRefGoogle Scholar
Ribet, K. A., Abelian varieties over Q and modular forms . In: Algebra and topology, Korea Advanced Institute of Science & Technology, Taejŏn, 1992, pp. 53–79.Google Scholar
Serre, J.-P., Sur les représentations modulaires de degré $2$ de ${\mathsf{Gal}} (\overline{\ {\mathsf{Q}}}/ {\mathsf{Q}})$ . Duke Math. J. 54(1987), 179–230. http://dx.doi.org/10.1215/S0012-7094-87-05413-5 Google Scholar
Serre, J.-P., Abelian l-adic representations and elliptic curves. 2nd ed., Advanced Book Classics Addison-Wesley Publishing Company, Advanced Book Program, Redwood City, CA, 1989.Google Scholar
Shimura, G., The special values of the zeta functions associated with Hilbert modular forms . Duke Math. J. 45(1978), 637–679.CrossRefGoogle Scholar
Shimura, G., Introduction to the arithmetic theory of automorphic functions. Publications of the Mathematical Society of Japan, 11, Reprint of the 1971 original, Kanô Memorial Lectures, 1, Princeton University Press, Princeton, NJ, 1994.Google Scholar
Skorobogatov, A., Torsors and rational points . Cambridge tracts in mathematics, 144, Cambridge University Press, Cambridge, UK, 2001. http://dx.doi.org/10.1017/CB09780511549588 Google Scholar
Stoll, M., Finite descent obstructions and rational points on curves . Algebra Number Theory 1(2007), 349–391. http://dx.doi.org/10.2140/ant.2007.1.349 CrossRefGoogle Scholar
Taylor, R., On Galois representations associated to Hilbert modular forms . Invent. Math. 98(1989), 265–280. http://dx.doi.org/10.1007/BF0138853 CrossRefGoogle Scholar
Taylor, R., Remarks on a conjecture of Fontaine and Mazur . J. Inst. Math. Jussieu 1(2002), 125–143. http://dx.doi.org/10.1017/S147474800200038 CrossRefGoogle Scholar
Tunnell, J., Artin’s conjecture for representations of octahedral type . Bull. Amer. Math. Soc. 5(1981), 173–175. http://dx.doi.org/10.1090/S0273-0979-1981-14936-3 CrossRefGoogle Scholar
Ullmo, E., Points rationnels des variétés de Shimura . Int. Math. Res. Not. 2004(2004), no. 76, 4109–4125. http://dx.doi.org/10.1155/S1073792804140415 CrossRefGoogle Scholar