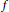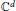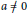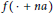Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Gauthier, Paul M.
and
Shirazi, Mohammad
2022.
Asymptotic first boundary value problem for holomorphic functions of several complex variables.
Canadian Mathematical Bulletin,
Vol. 65,
Issue. 2,
p.
361.
Meyrath, Thierry
2022.
Common Universal Meromorphic Functions for Translation and Dilation Mappings.
Computational Methods and Function Theory,
Vol. 22,
Issue. 4,
p.
781.
Guo, Bin
and
Xie, Song-Yan
2024.
Universal holomorphic maps with slow growth I: an algorithm.
Mathematische Annalen,
Vol. 389,
Issue. 4,
p.
3349.